Механика гидро - и пневмоприводов
Математическая модель силовой части гидропривода с объемным регулированием
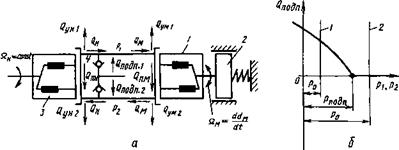
Силовая часть гидропривода с объемным регулированием состоит из исполнительного двигателя с поступательным или вращательным движением выходного звена и объемного насоса с изменяемой подачей. Чтобы познакомиться с особенностями математического описания процессов в гидродвигателях при неограниченном вращательном движении выходного звена, т. е. в гидромоторах, рассмотрим схему, изображенную на рис. 5.4, а. На схеме вал аксиально-поршневого гидромотора 1 соединен с нагрузкой 2. Рабочая жидкость поступает в гидромотор от аксиально-поршневого насоса 3, подача которого может изменяться как по величине, так и по направлению путем регулирования угла 7Н наклона шайбы. В соответствии со схемой движение жидкости происходит по замкнутому гидравлическому контуру, причем так, что у насоса либо верхняя гидролиния является напорной, а нижняя — всасывающей, либо наоборот. Для компенсации утечек жидкости предусмотрены клапаны 4, к которым подведена жидкость под давлением Рподп подпитки от вспомогательного насоса. Расходная характеристика этих клапанов приведена на рис. 5.4, б.
|
Рис. 5.4. Схема силовой части гидропривода с объемным регулированием (а) и характеристика (б) подпиточных клапанов |
При давлении р < рПодп открывается верхний клапан, пропуская жидкость (расход фподп 1) в гидролинию с давлением р1, при р2 < Рподп открывается нижний клапан, и расход Фподп 2 поступает в гидролинию с давлением р2. Если давление Рподп меньше одного из указанных давлений, то соответ
Ствующий клапан закрыт, а если рПодп < Р и рПодп < Р2> то закрыты оба клапана (ро на прямой 2 рис. 5.4, б). В точке, для которой р = р2 = Рподп) характеристика имеет разрыв по первой производной и поэтому в данной точке не может быть линеаризована методом малых отклонений. С целью получения линейной математической модели силовой части гидропривода с объемным регулированием предположим, что при выбранном для исследования режиме работы привода (р = р2 = Ро на прямой I) клапаны открыты и соответственно
Фподп 1 = &кл(Рподп “Р1); (5.50)
Фподп2 — &кл(Рподп ""Р2)) (5.51)
Где ккл — проводимость клапана.
Для момента времени, при котором вследствие малого отклонения шайбы насоса от среднего положения жидкость поступает из насоса в гидролинию с давлением р, а из гидролинии с давлением р2 уходит в насос, запишем следующие уравнения расходов:
Як — Ям + Яп. к + Яп. м +
“I" Яу. к 1 “I" Яу. м 1 “Ь Ясж1 ~~ Фподп 15 (5.52)
Фн — Фм + Фп. н + Фп. м"“
Фу. н2 Фу. м2 Фсж2 "I" Фподп2* (5.53)
В уравнениях (5.52) и (5.53) расходы фСж1 и Фсж2 являются теми составляющими подачи фн насоса, которые связаны с сжимаемостью жидкости. Остальные составляющие фн, показанные на схеме (см. рис. 5.4, а) стрелками, учитывают расход фм, обеспечивающий вращение вала гидромотора, а также утечки и перетечки жидкости в насосе и гидромоторе. Уравнения упрощается, если насос и гидромотор имеют одинаковые размеры и изготовлены с одинаковыми допусками. В этом случае можно принять, что
Фп. н — фп. м — Фпер> Qy. nl — Фу. м1 — Фут1> Фу. н2 ~ Фу. м2 ~ Фут2*
|
Фпер = ^пер(р1 Р2)) Фут1 = кутР1) Фут 2 = ^утР2> |
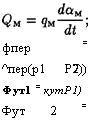 Перечисленные составляющие фн определяют с помощью следующих соотношениий:
Перечисленные составляющие фн определяют с помощью следующих соотношениий:
(5.54)
(5.55)
(5.56)
(5.57)
Где дм = Ум/(2тг) — рабочий объем гидромотора, отнесенный к одному радиану угла поворота его вала; А? пер — проводимость зазоров, по которым в насосе и гидромоторе происходят перетечки жидкости из камер с высоким давлением в камеры с низким давлением; кут — проводимость зазоров в насосе и гидромоторе, по которым происходит утечка жидкости.
Предполагая, что гидролинии выполнены из трубопроводов с одинаковыми проходными сечениями и имеют одинаковую длину, а также считая стенки трубопроводов абсолютно жесткими, запишем
|
(5.58) |
![]() Уо_<1р1
Уо_<1р1
Фсж1 — р м ’
Ж и»
|
(5.59) |
![]() Уо <1р 2
Уо <1р 2
Ясж2 ~ Вж <И
Где Уо — внутренний объем одного трубопровода вместе с подключенными к нему камерами насоса и гидромотора; Вж — модуль объемной упругости жидкости.
Соотношения (5.58) и (5.59) записаны исходя из того, что давление во всех сечениях каждого трубопровода изменяется одновременно, а инерция жидкости и гидравлическое сопротивление трубопроводов незначительно влияют на эти изменения давления. Такое допущение позволяет получить математическую модель силовой части гидропривода в сосредоточенных параметрах, которая описывает происходящие в приводе процессы с достаточной для практики достоверностью, если характерное время процесса приблизительно на порядок больше времени распространения волны давления по длине трубопровода. В противном случае может возникнуть необходимость использования более сложной математической модели привода с распределенными параметрами.
Подставив составляющие Як из соотношений (5.50), (5.51), (5.54) - (5.59) в уравнения (5.52) и (5.53), а затем сложив эти уравнения, получим
(1рм. ^ 9м И +2В^~М+кзРм~®н’ (5’60)
ГДе Рм = Р1 ~~ Р2 к5 — куТ + 2А:пер Н —.
Геометрическую подачу Як аксиально-поршневого насоса можно найти по соотношению
^ ^7н /с *1Ч
Я н — — , (5.61)
Где 5П — рабочая площадь поршня (плунжера); гп — число поршней; Вп — диаметр цилиндрической поверхности, на которой расположены оси поршней; Пн — угловая скорость вала насоса.
При малых изменениях угла наклона шайбы насоса около ее среднего положения и постоянной скорости вращения вала насоса соотношение (5.61) нетрудно линеаризовать и представить в виде
Як = (5.62)
Где = 5,п^п^п^н/2тг — коэффициент преобразования угла наклона шайбы в подачу насоса.
После подстановки величины фн из соотношения (5.62) в уравнение (5.60) получим
+ ^Б~Р---------- 1Г + 17— Рм = 7н - (5.63)
КЯ1 (1Ь Ль Кц*у
В уравнение (5.63) входит разность рм давлений в камерах гидромотора, которая также входит в уравнение движения вала гидромотора
3 ^2 ~ 9мРм Миоз — Мтр 1 — AfXp2, (5.64)
Где «/ — приведенный к валу гидромотора момент инерции управляемого приводом объекта, вычисленный с учетом момента инерции ротора самого гидромотора; Мпоз — момент от действия на вал гидромотора позиционной нагрузки; Мхр 1 и Мтр 2 — моменты сил трения соответственно в гидромоторе и нагрузке, приложенной к валу гидромотора.
Нагружающие вал гидромотора моменты определим следующими соотношениями:
Мпоз = ^ПОЗ^М) (5.65)
Подставив в уравнение (5.64) моменты из соотношений (5.65)-
(5.67) , получим
J в? ам ктр (1ам кпоз. V
---- трг + лГ +---------------- ам = Р™' (5‘68)
Ям & аЛ
Где А? хр — ^тр 1 "Ь ^тр2-
Уравнения (5.63 ) и (5.68) сведем к одному уравнению, описывающему динамические процессы в силовой части гидропривода с объемным регулированием, которое представим в виде
, <Рам (1ам, д0ч
А1"^Г а°ам = 7н’ ^
|
■О |
![]() Где аз — ——; а,2 — —----------------- —---- 1--- ——; а — ( 1 +
Где аз — ——; а,2 — —----------------- —---- 1--- ——; а — ( 1 +
2ВждмК(2*у 2 ВждмК(2^
^поз Уо А?8А? Хр А?8А?
ПОЗ Г)
+ ——Т) Н---- ) ——; ао = —7?—• Величины, стоящие в
25ж9Й 9м / Яу ЯмКЯу
Скобках при вычислении коэффициента ах, обычно малы по сравнению с единицей и поэтому в дальнейшем их можно не учитывать. С таким допущением преобразовав по Лапласу уравнение (5.69) при нулевых начальных условиях, получим уравнение, которое представим в виде
Тт. о$(Тмз2 + 2£МТМ6 + 1)ам(б) =
== 7н(5) - Кп. о^м^)) (5.70)
Где
Гг. о = (5.71)
Яч
Ги=(572) Г _ УЯж*8 + 0,5^0 /С 70
А-,.. = Цр-- (5.74)
Чм^7
Коэффициенты уравнения (5.70), вычисляемые по формулам (5.71) - (5.74), отражают физические явления, аналогичные тем, которые рассматривались в двух предыдущих математических моделях и имеют с ними схожие названия: Гг. о — постоянная времени гидропривода с объемным регулированием; Тм — постоянная времени нагруженного гидромотора, равная обратному значению собственной частоты м гидромотора; См — коэффициент относительного демпфирования гидромотора; ККг0 — коэффициент внутренней обратной связи, вызванной действием позиционной нагрузки и негерме - тичностью гидромашин (гидромотора и насоса).
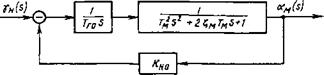
Уравнению (5.70) соответствует изображенная на рис. 5.5 структурная схема. Сравнивая данную структурную схему со структурными схемами силовых частей гидропривода с
|
Рис. 5.5. Структурная схема силовой части гидропривода с объемным регулированием |
|
|
||
|
|||
|
|||
Рис. 5.6. Структурная схема силовой и управляющих частей гидро - или пневмопривода
Дроссельным регулированием и пневмопривода, нетрудно заметить, что они различаются только величинами, определяющими значения постоянных времени и коэффициентов относительного демпфирования. Это делает возможным структурную схему гидро - или пневмопривода представлять в виде последовательного соединения (рис. 5.6) силовой части с передаточной функцией И'с. ч^) и управляющей части с передаточной функцией №у. ч(з). Первая передаточная функция находится либо согласно правилам преобразования рассмотренных ранее структурных схем, либо непосредственно из математических моделей силовых частей приводов.
Передаточная функция управляющей части описывает динамические свойства устройств, используемых в приводе для управления исполнительным двигателем. Из всего многообразия управляющих устройств ниже выбраны такие, которые, во-первых, широко применяют в гидро - и пневмоприводах различного назначения и, во-вторых, позволяют в достаточной мере наглядно изложить общую методику математического моделирования такого вида устройств.