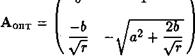Механика гидро - и пневмоприводов
Переходные процессы в гидро — и пневмоприводах
Показатели качества переходных процессов
Системы с гидро - и пневмоприводами во время эксплуатации подвергаются как управляющим, так и возмущающим воздействиям, в результате которых происходят изменения состояния систем во времени. В реальных условиях воздействия на систему чаще всего бывают случайными, вызывая в системе случайные или стохастические процессы. На практике сведения о характеристиках случайных воздействий на системы с гидро - и пневмоприводами, как и на многие другие технические системы, обычно крайне ограничены, поэтому при исследованиях динамических свойств систем широко применяют так называемые детерминированные воздействия. Типовыми детерминированными воздействиями являются: ступенчатое, импульсное и гармоническое. При последнем виде воздействия рассматривают поведение системы в частотной области сигналов, в которой достаточно эффективно можно решать задачи устойчивости систем, а также исследовать влияние различных факторов на динамические характеристики отдельных элементов и систем в целом.
В частотной области сигналов хорошо сочетаются рассчитанные по математическим моделям характеристики части устройств исследуемой системы с экспериментальными характеристиками тех устройств, для которых по каким-либо причинам математические модели не могли быть составлены. Благодаря отмеченным достоинствам методы исследований и расчетов систем в частотной области сигналов широко используют на практике. Однако если при гармонических воздействиях сравнительно просто провести испытания отдельных устройств и какой-то части системы, то натурные испытания систем, содержащих сложные объекты (энергетические установки, летательные аппараты, строительно-дорожные машины), далеко не всегда осуществимы.
В связи с чем наряду с частотными методами не менее широко применяют методы исследований и расчетов систем во временной области. При этом определяют переходные процессы, вызванные в системах ступенчатыми или импульсными воздействиями. Первые из них проще воспроизвести в реальных условиях, что облегчает проверку адекватности рассчитанных и полученных в результате физических экспериментов переходных процессов. К тому же процессы при ступенчатом воздействии на систему дают достаточно наглядное представление о таких динамических свойствах систем, как быстродействие, колебательность и продолжительность процесса.
Если линейная математическая модель системы в необходимой мере отражает динамику реальной системы, то по переходным процессам при ступенчатых воздействиях можно вычислить переходные процессы при импульсных воздействиях,
А также найти те и другие по частотным характеристикам системы.
При наличии в системе существенно нелинейных звеньев такой пересчет процессов будет приближенным и не исключает получения неверных результатов.
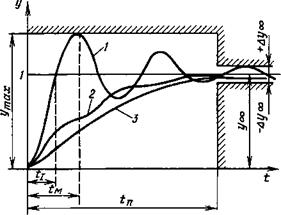
На рис. 6.16 изображены основные виды переходных процессов, вызванных ступенчатыми воздействиями на систему, математическая модель которой близка к линейной. Переходный процесс 1 называют колебательным, переходный процесс 2 — монотоннным, переходный процесс 3 — апериодическим. В устойчивой системе, описываемой линейным дифференциальным уравнением, выходная величина у приближается к своему установившемуся значению уж при < —> оо, поэтому продолжительность переходного процесса оценивают по значению времени <П) при котором значения у отличаются от Уоо на ±Ау00. Эта величина определяет “канал” допустимых отклонений у, при которых процесс считается закончившимся. Для колебательного процесса кроме указывают время первого согласования изменяющегося значения у со своим установившимся значением уоо. Чем меньше тем выше быстродействие системы. Показателем колебательности процесса является число периодов Гпер, находящихся в пределах времени Обычно считают, что это число не должно быть более 1,5 ... 2,0. Важной величиной, характеризующей колебательный процесс, является максимальная динамическая ошибка (при Ь = Ьм)
Отах = —Х ~-—100 %, (6.112)
Уоо
Которая для большинства систем не должна превышать 25 ... ...30%.
Время переходного процесса, размер “канала” допускаемых отклонений выходной величины и максимальная динамическая ошибка определяют границы области (отмечены на рис. 6.16 штриховкой), в которой должен располагаться график допускаемого для системы переходного процесса.
Монотонный и апериодический переходные процессы оценивают по времени <п - У одной и той же системы при разном
|
Рис. 6.16. Различные виды переходных процессов |
Выборе параметров, влияющих на вид переходного процесса, значение получается больше при апериодическом или монотонном процессе, чем в случае колебательного процесса. Поэтому наибольшее быстродействие достигается в системе с колебательным процессом. Если быстродействие несущественно, а необходимо обеспечить плавный переход системы из одного состояния в другое, то апериодический процесс будет лучше коле бательного.
Для качественного управления объектом важны не только вид и показатели переходных процессов, но и точность, с которой при заданных входных воздействиях устанавливаются значения выходных величин. Точность управления системами с гидро - и пневмоприводами зависит от многих факторов, к числу которых относятся силы сухого трения, действующие на отдельные элементы приводов, утечки рабочих сред в управляющих устройствах и исполнительных двигателях, люфты в механических соединениях, электромагнитный гистерезис в электромеханических преобразователях сигналов и др. Но даже при совершенном исполнении всех устройств гидро - и пневмопривода, практически исключающих все подобные факторы, точность управления во многом будет предопределена
той структурой системы, которую можно описать линеинои математической моделью. Чтобы пояснить это утверждение, рассмотрим сначала применяемый в теории управления метод оценки ошибок при установившихся режимах систем.
С этой целью воспользуемся структурной схемой, изображенной на рис. 4.2, в, и передаточной функцией (4.61), из которых при отрицательной обратной связи получим
С(5,=тжмм,)' (6Ш)
Если входное воздействие является ступенчатым (см. рис. 6.17), то
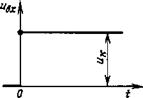 £^вх(0
£^вх(0
Рис. 6.17. График ступенчатой функции
Изображение по Лапласу функции (6.114) найдем по формуле (4.45):
|
О — 3% |
![]()
Оо
= (6.115)
5
С учетом изображения (6.115) формулу (6.113) представим в виде
+ (6'Ш) В соответствии со свойством преобразования Лапласа значение функции оригинала /(<) при t —> оо можно вычислить по изображению Р(з) при 5 —► 0 с помощью равенства пределов
Нш /(<) = Нш зР(з).
*—юо з—►О
Обозначив установившуюся ошибку 6уст и применив формулы (6.116) и (6.117), найдем
<уст - йо L + H'wVo. cM' (вл18)
Следящие гидро - и пневмоприводы в большинстве случаев имеют отрицательные обратные связи по положению выходного звена. Для таких приводов примем, что
^о. с(5) = - Кп. ОС -
Кроме того, структурные схемы силовых частей приводов, как было показано в главе 5 (см. рис. 5.3 и 5.5), могут содержать интегрирующее звено. Если для этих силовых частей значение коэффициента внутренней обратной связи (Кк или Кн) пренебрежимо мало, а управляющая часть не содержит интегрирующих звеньев, то используя формулу (6.118), можно получить
(вл19)
Где Ку — коэффициент усиления всего разомкнутого контура, значение которого возрастает с увеличением добротности силовой части привода и коэффициента усиления управляющей части.
Из соотношения (6.119) следует, что при наличии в контуре привода интегрирующего звена £уст = 0, когда UK = const. При изменении UK с постоянной скоростью, т. е. dUK/dt = = const, движение выходного звена происходит с постоянной ошибкой по скорости. Эта ошибка будет тем меньше, чем больше значение коэффициента Ку. Последнее обстоятельство объясняет причину, по которой может потребоваться увеличить значение добротности привода. Кроме того, с увеличением добротности привода обычно возрастает его быстродействие. Однако повышение добротности ограничено условием устойчивости, что, в частности, показывает неравенство
(6.14).
Если коэффициент (Кя или Kni) внутренней обратной связи у силовой части привода нельзя принять равным нулю,
То передаточная функция разомкнутого контура привода при 5 —> 0 будет приближаться к апериодическому звену первого порядка, а не к интегрирующему звену. В этом случае установившаяся ошибка определяется соотношением
^уст = (6.120)
Где К — коэффициент усиления всего разомкнутого контура привода, не содержащего интегрирующее звено.
В соответствии с формулой (6.120) для уменьшения установившейся ошибки в конце переходного процесса, вызванного ступенчатым воздействием, необходимо увеличивать коэффициент усиления разомкнутого контура. Однако, как и в предыдущем случае, такое увеличение коэффициента усиления свыше определенного значения нарушает условие устойчивости привода.
Выбор параметров и расчет переходных процессов
При проектировании систем с гидро - и пневмоприводами необходимо выполнять противоречащие друг другу условия, по которым для обеспечения высокого быстродействия и малых установившихся ошибок следует увеличивать коэффициент усиления разомкнутого контура привода, а для сохранения устойчивости системы — не превышать допустимых для этого коэффициента значений.
Параметры привода, удовлетворяющие указанным условиям, предварительно можно выбрать с помощью ЛАХ и ЛФХ разомкнутого контура так, чтобы обеспечивались рекомендуемые запасы по фазе и амплитуде (см. § 6.1).
Если наибольшая из постоянных времени управляющей части привода на порядок меньше любой из постоянных времени силовой части, то для приближенного выбора параметров привода можно воспользоваться графиками, разделяющими плоскость коэффициентов характеристического уравнения, записанного в предложенной И. А. Вышнеградским форме. Эти графики приведены на рис. 6.18.
Параметры А и В являются коэффициентами уравнения
И 2 И 5 6 7 6 9 10 11А Рис. в.18. Области параметров системы третьего порядка при различных видах переходных процессов
В которое можно преобразовать характеристическое уравнение рассматриваемой системы
Аз А3 а>22 И - а^А -1- ао = 0, (6.121)
Вводя новую переменную
И используя соотношения
А = -^==; (6.122)
В = —(6.123)
Формулы (6.122) и (6.123) позволяют найти по параметрам А и В, которые соответствуют указанным на графиках переходным процессам, значения двух коэффициентов характеристического уравнения (6.121) при известном третьем коэффициенте.
Например, в случае следящего гидромеханического привода с дроссельным регулированием, для которого были получены характеристическое уравнение (6.12) и условие устойчивости (6.14), формулы (6.122) и (6.123) имеют вид
|
|
По соотношениям (6.124) и (6.125) можно, выбрав параметры А и Б с учетом требуемого переходного процесса и вычислив по формуле (5.27) постоянную времени Тц, найти коэффициент £ц относительного демпфирования и добротность Бт гидропривода. Затем с помощью формул (5.29) и (6.15) можно рассчитать коэффициенты линеаризованной расходно - перепадной характеристики золотникового устройства, а по ним получить его основные размеры. Коэффициент Кос обратной связи обычно известен заранее, так как от него зависит перемещение выходного звена привода, которое вызывает заданное значение входного сигнала.
В современных методах теории управления для расчетов на ЭВМ переходных процессов применяют различные программы. Одни из таких программ основаны на математических моделях, представленных в виде уравнений вход-выход, другие — на математических моделях, описывающих рассматриваемые системы в переменных состояния. Первого вида программы обычно предусматривают использование структурных схем как линейных, так и нелинейных систем, причем в обоих случаях все переменные являются функциями времени, а не их изображениями по Лапласу. В связи с чем величина
5, которая в передаточных функциях звеньев таких структурных схем уже не является переменной в преобразовании Лапласа, должна рассматриваться как оператор дифференцирования, т. е. в = р1 (см. гл. 4).
Очень важно также иметь в виду, что при расчете по линейным математическим моделям входные воздействия не должны превышать те значения, при которых какая-либо из переменных может быть реально осуществимой в данной системе. Это условие необходимо учитывать особенно в тех случаях, когда при расчете используются размерные значения переменных. В случае применения безразмерных переменных и
правильном выборе базовых величин при нормировании уравнений данное условие автоматически выполняется.
Для примера перейдем к безразмерным переменным в математической модели электрогидравлического следящего привода, структурную схему которого получим, объединив структурные схемы силовой части гидропривода с дроссельным регулированием (см. рис. 5.3, а) и электрогидравлического усилителя (см. рис. 5.10). В результате будем иметь структурную схему, изображенную на рис. 6.19, где Кп, ос — коэффициент преобразователя сигналов обратной связи от выходного звена (перемещение штока гидроцилиндра) к входу электронного усилителя с коэффициентом Кус.
|
|
|
|
|
|
|
|
Кррі+Кур+Крух
I-__________ т'——А
Ллос
Рис. 6.19. Структурная схема электрогидравлического следящего привода
Безразмерные переменные обозначим чертой сверху, а базовые величины — верхним индексом При этом размерные и безразмерные переменные будут связаны соотношениями:
Иъх = ^вхивх ие = иеие 1 = ФяЪФяЪ Ф* = ФяФя') х3 = х*хъ ушт = ушхушх; ^я1 ~
Чтобы после перехода к безразмерным величинам не произошло искусственного изменения коэффициента усиления разомкнутого контура системы, значения базовых величин необходимо согласовать между собой. Для этого за основную базовую величину примем перемещение золотника X* = я3.шах-
Тогда
|
* * *у UBX = «е = к V. ; Лусл*м I* - ^1- У ~ К ’ — ^ВХ. |
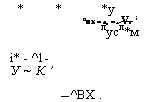
|
2/шт — |
![]()
|
*п. ос 1 + ■К'я^.К'осЛ "i" КрруКрух) *# |
![]()
|
^я1 “ IV' ^3 5 Лх(р ¥>я = |
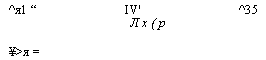
|
Хз |
В безразмерных переменных математическое описание отдельных участков структурной схемы можно представить следующими уравнениями:
<Ря’1~ TyS + l Ue’
1 ~ T%s + 2№ + 1 Ve;
_ _
Хз = vпп^;
1 ЯuiT_T252 + 2Cur45 + lяi;
_ #4-
Y' = TTsX>'
Ue = иВх ~ ^п. о.с^5Ушт!
'fie = ^6 ^«,1 ~ (Koc.1 "i" KtppyKpyx)K$X3.
В эти уравнения входят дополнительные коэффициенты, обеспечивающие согласование базовых величин и имеющие следующие значения:
*i = <xMi; *2 = v*/*о; Кз = хУ<р*я) Ki = x*jy*;
КЬ = я7<x; JT6 = Vhlvl
При расчете переходного процесса, вызванного ступенчатым воздействием, по математической модели привода с безразмерными переменными значение ^вх можно принять единичным ступенчатым. В теории управления такое воздействие (единичный скачок) обозначают функцией 1(/). Однако в данном случае
ПЪХ — 1(0
Вызовет безразмерное перемещение золотника х3 = 1, что соответствует язтах. Если переходный процесс будет колебательным, то в какие-то моменты времени получатся значения х3 > 1, что может противоречить условию применимости линейной модели привода. Поэтому с запасом на максимальную динамическую ошибку при переходном процессе правильнее принять иъх = 0,65... 0,75.
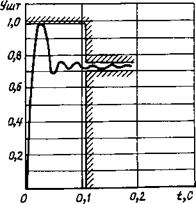
На рис. 6.20 показан график переходного процесса, рассчитанный для электрогидравлического следящего привода по модели с безразмерными переменными (штриховкой ограничены области, выделенные на рис. 6.16). Чтобы получить размерные значения входной и выходной величин, их безразмерные значения следует умножить на базовые величины.
|
Рис. 6.20. Переходный процесс, рассчитанный по безразмерной математической модели электрогидравлического следящего привода |
Если для расчета переходного процесса предполагается применить типовые программы для решения дифференциальных уравнений, то рассмотренную математическую модель (при s = d/dt) можно привести к системе уравнений, записанных в форме Коши. Аналогично составляют в безразмерном виде нелинейные математические модели систем с гидро - и пневмоприводами.
Переходные процессы, полученные для одной и той же системы с разными значениями отдельных параметров, а также для различающихся по конструктивному исполнению систем, сравнивают либо по указанным в начале параграфа показателям (<7щах>*п>£уст)> либо с помощью интегральных оценок. Достаточно распространена оценка в виде интеграла
|
Оо
О |
Где <т — модуль текущей динамической ошибки, для системы с приводом а = у — ук; ук — установившееся значение координаты выходного звена, в отсутствие установившейся ошибки Ук — Уоо •
Синтез обратных связей в системах с приводами
С интегральными оценками процессов связаны решения задач оптимального управления различными системами. Для линейной системы, описываемой уравнениями (см. гл. 4)
|
(6.126) (6.127) |
![]() Dx а / . ✓
Dx а / . ✓
У = С («)х,
При начальных условиях х(*о) = хо задача оптимального управления состоит в том, чтобы найти управление иОПт(0> обеспечивающее минимум функционала где (%' = <Э'(<) и К = Щ*) — положительно определенные симметричные матрицы при < і < *к! Рі — неотрицательно определенная симметричная матрица.
В такой постановке задачи предполагается, что А(<) есть непрерывная функция времени, а В (і), С(/), Q,(^), И(<) — кусочно-непрерывные функции времени, кроме того, все эти матричные функции ограничены.
Наиболее сложно выбрать матрицы Рі, Q/ и К, которые в функционале (6.128) являются матрицами весовых коэффициентов. Для определения этих матриц выделяют интегральную квадратичную ошибку управления
Интегральную квадратичную входную переменную
J (итКи)(И
И квадратичную терминальную ошибку, характеризующую конечное состояние системы (при / = /к). Затем матрицы весовых коэффициентов назначают исходя из допустимых средних квадратичных ошибок и допустимых значений входной переменной.
При решении задачи о выборе оптимальных обратных связей (регуляторов) функционал (6.128) представляют в виде
Ік
1= у*(хт<3х + итКді) <И + хт(/к)Ріх(/к), (6.129)
О
Где <3 = (^(^(^'(^С^) — неотрицательно определенная симметричная матрица.
Решение может быть получено на основе принципа максимума Понтрягина и другими методами, подробно рассмотренными в теории управления. При решении учитывают, что в случае управления с обратной связью существует зависимость
Вектора u(t) от вектора х(/). Эту зависимость получают с помощью симметричной матрицы Р(/) изменяющихся во времени коэффициентов. Для определения матрицы Р(/) используют уравнение
^ = - РА(0 - АТ(*)Р + PB(*)R-1BTP - Q (6.130) dt
С граничными условиями P(tK) = Pl-
По аналогии с обыкновенным дифференциальным уравнением для одной зависимой переменной матричное дифференциальное уравнение (6.130) называют уравнением Риккати. Это уравнение в соответствии с заданным граничным условием решают в интервале времени от tK до <о = 0. Задача упрощается, если матрицы А, В, С, Q и R не зависят от времени, а поведение системы рассматривается в большом интервале времени. Тогда верхний предел интеграла (6.129) можно принять равным бесконечности, а Р = 0. В результате матричное дифференциальное уравнение (6.130) становится алгебраическим уравнением
РА + АТР - PBR_1BTP + Q = 0. (6.131)
После того, как вычислена матрица Р, оптимальное управление определяется уравнением
И = - Кх, (6.132)
Где К = R-1BTP
Рассмотрим в качестве примера задачу об оптимальном управлении выходным звеном гидропривода с дроссельным регулированием. Предположим, что параметры привода позволяют пренебречь сжимаемостью рабочей среды. При этом условии уравнение (5.24) можно упростить и записать в виде
![]() ^Ушт. Зц ^Ушт 1 QO
^Ушт. Зц ^Ушт 1 QO
К,(ет)
Воспользуемся следующими переменными состояния:
Dx 1
Ушт — ^ — х2
И представим уравнение (6.133) системой двух уравнений йх 1
-Ж = хг’
<1x2 _ -^п ,
<Й "г-Й'рр Х2 К<Эрт Хз'
|
А Г° 1 ^ 5п А = , где а = —— � —а/ тКп |
![]() Для этой системы
Для этой системы
^<?Р
Вследствие того, что система имеет одну входную величину и = х3 и одну выходную величину 2/шт = у, матрица В редуцируется в вектор-столбец
ь) ’ Где “ КЯрт ’ а уравнение выхода имеет вид
Для данной системы уравнение (6.131) представим в виде
Р(2 Л)+(! -°<1)1>-р(б) ?(0 Ь)1>+
|
+ Где |
![]() (£) (1 0) = 0, (6.134)
(£) (1 0) = 0, (6.134)
_ (Р11 Р12 Л.
Р21 Р22/
Г — весовой коэффициент, учитывающий энергетические затраты на управление.
Удовлетворяющие решению уравнения (6.134) элементы матрицы Р определяют соотношения:
Ф / 2 26 Ри = туа +^;
Р12 = Р21 = - у;
Согласно уравнению (6.132), для оптимального управления гидроприводом необходимо, чтобы
Х3 = —Кх,
Где
|
|
|
|
![]()
![]()
Компонентами вектора х здесь являются перемещение ушт и скорость (1ушт/(И штока гидроцилиндра. Поэтому полученное значение К показывает, что при принятых выше допущениях для осуществления оптимального управления гидроприводом следует применить кроме обратной связи по перемещению выходного звена еще обратную связь по его скорости.
При таких обратных связях замкнутый контур гидропривода описывается уравнением
|
|
Где
|
|
|
/ о |
|
1 |
С учетом сжимаемости рабочей среды алгоритм оптимального управления гидроприводом может усложниться.
Рассмотренные в данном учебнике вопросы раскрывают основные особенности гидро - и пневмоприводов, вызванные взаимодействием их элементов с рабочими, средами, которое влияет на эффективность использования энергии, устойчивость и точность выполняемых приводами операций. К тому же гидро - и пневмоприводы представляют собой системы, процессы в которых существенно зависят как от характеристик
Отдельных устройств, так и от свойств, возникающих вследствие соединения устройств между собой. В связи с чем системный подход к задачам механики гидро - и пневмоприводов, описанный в учебнике, может быть полезен при их создании и использовании в различных машинах, аппаратах, станках и других технических объектах.