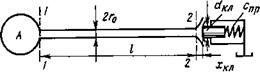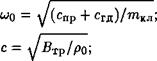Механика гидро - и пневмоприводов
Автоколебания в управляющих устройствах гидро — и пневмоприводов
Управляющие устройства вместе с силовой частью гидро - и пневмопривода образуют динамические системы, которые, как сказано в § 6.1, должны, прежде всего, удовлетворять условиям устойчивости. Если математическая модель системы представлена в линейном виде, то задачу устойчивости всей системы и отдельных ее частей можно успешно решить описанными в том же параграфе методами. Однако линейные математические модели не отражают полностью свойства реальных технических устройств и их применение на практике будет обоснованным, если характеристики составляющих элементов не выходят за рамки допущений, принятых при составлении моделей. Из анализа влияния основных нелинейностей на устойчивость гидро - и пневмоприводов (см. § 6.2) следует, что в следящем приводе могут возникать автоколебания, при которых выходное звено вместо того, чтобы занимать заданное сигналом управления положение, совершает незатухающие колебания.
Автоколебания могут возникать также в управляющих устройствах. При этом управление исполнительными гидро - и пневмодвигателями так ухудшится, что весь привод будет непригоден для использования. Кроме того, при автоколебаниях возрастает вероятность преждевременного разрушения элементов устройства. Автоколебания управляющих устройств, применяемых для регулирования источников энергопитания, сопровождаются периодическими изменениями давлений в гидро - и пневмоприводах, что может вывести из строя всю систему.
Автоколебания в управляющих устройствах обычно происходят в случае взаимодействия подвижных механических элементов (золотников, клапанов, заслонок, струйных трубок) с потоками рабочих сред. Но могут иметь место и в устройствах без подвижных механических элементов в результате взаимодействия между собой потоков рабочей среды, вытекающей из различных каналов, а также из-за неустойчивости течения в ограниченных твердыми стенками камерах. Не имея возможности рассмотреть здесь все эти устройства, остановимся на наиболее распространенных из них и позволяющих, к тому же, изучить достаточно общие закономерности возникновения автоколебаний. К таким устройствам относятся золотники, заслонки и клапаны.
Автоколебания золотников
Как показано в главе 3, к золотникам со стороны потока рабочей среды приложены гидродинамические силы, которые,
І
|
7 |
|
|
|
Рсл |
|
А Ргд <1 Рпр
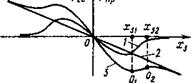
6 Рис. 6.6. Золотниковый распределитель (а) и зависимость гидродинамической силы от смещения золотника (б) |
|
Спр рп В |
 В общем случае, зависят от формы и расположения границ потока, а также от направления течения среды. Для оценки возможных состояний золотника воздействие потока среды представим нелинейной зависимостью гидродинамической силы Ргд от перемещения золотника я3, схема которого дана на рис. 6.6, а. График такой зависимости показан кривой 1 на рис. 6.6, б.
В общем случае, зависят от формы и расположения границ потока, а также от направления течения среды. Для оценки возможных состояний золотника воздействие потока среды представим нелинейной зависимостью гидродинамической силы Ргд от перемещения золотника я3, схема которого дана на рис. 6.6, а. График такой зависимости показан кривой 1 на рис. 6.6, б.
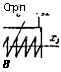
Учитывая нелинейность функции - Ргд(яз) вместо уравнения (3.57) запишем уравнение движения золотника в более общем виде
|
|
Где А;тр — коэффициент вязкого трения, вызванного движением среды в зазоре между золотником и гильзой; ккк — коэффициент, вычисляемый по формуле (3.60); спр — жесткость каждой из пружин, нагружающих золотник силой Рпр в осевом направлении (см. рис. 6.6, б прямая 2); и — управляющее воздействие на золотник, создаваемое разностью ру — Ру 2 давлений в торцовых полостях А и В.
Введем переменные состояния, обозначив
/1 <т*
X 2 — х3)
|
|
|
И заменим уравнение (6.44) системой двух уравнений (1х |
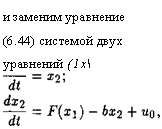 (6.45)
(6.45)
(6.46)
Где
|
|
Га3
2сПрЖ3 -Ргд(‘^з)<
|
|
|
И
|
|
(6-47) |
![]() Система (золотник), описываемая уравнениями (6.45) и
Система (золотник), описываемая уравнениями (6.45) и
(6.46) , при различных фиксированных значениях г^о будет иметь ряд возможных состояний равновесия, при которых (1х/<И = <1x2/Л = 0. На фазовой плоскости координаты точек равновесия найдем из уравнения
Щ + р(яь) = 0.
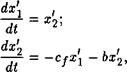 Эти точки являются особыми, их тип можно определить из анализа решений, линеаризованных в окрестности х = х3, х2 = х2з уравнений (6.45) и (6.46). График нелинейной функции Р(х) будет таким же, как кривая 3 на рис. 6.6, б, которая получена для га3Р(я 1) сложением ординат точек кривых 1 и 2. После линеаризации функции Р(х) в окрестности особой точки имеем
Эти точки являются особыми, их тип можно определить из анализа решений, линеаризованных в окрестности х = х3, х2 = х2з уравнений (6.45) и (6.46). График нелинейной функции Р(х) будет таким же, как кривая 3 на рис. 6.6, б, которая получена для га3Р(я 1) сложением ординат точек кривых 1 и 2. После линеаризации функции Р(х) в окрестности особой точки имеем
|
Где |
![]() (6.48)
(6.48)
Х=Х3
12=0
Системе уравнений (6.48) и (6.49) соответствует характеристическое уравнение
А2 ЬХ су = 0. (6.50)
Значения корней уравнения (6.50) зависят от параметров Ь и су. Вблизи среднего положения золотника, как показывает кривая 3, су > 0, параметр Ь может быть положительным, отрицательным или равным нулю.
Первый случай будет при &тр > 0, если коэффициент кик положительный (/х > /2)5 или отрицательный (/1 < /2)5 но по абсолютной величине меньше, чем ктр, а также в случае кин = 0, (/1 = /2)- Второй — при отрицательном значении А;ин, если он по абсолютной величине больше кТр. Третий — при ^тр “Ь &ин — 0.
Если 6 > 0, су > 0, то корни уравнения (6.50) — комплексные числа с отрицательной вещественной частью при Ь2 < 4су или отрицательные вещественные числа при Ь2 > 4су. Особую точку называют устойчивым фокусом и устойчивым узлом соответственно. Если 6 = 0, су > 0, то корни уравнения (6.50)
— чисто мнимые сопряженные комплексные числа, и особая точка — центр. Если 6<0,су>0, то при Ь2 < 4су особая
Точка — неустойчивый фокус; при Ь2 > 4су особая точка — неустойчивый узел.
При названных типах особых точек возможны следующие процессы: затухающие колебания золотника в окрестности его среднего положения, апериодическое возвращение предварительно смещенного золотника к среднему положению, незатухающие колебания золотника с амплитудой, равной его начальному отклонению, уход золотника от среднего положения с расходящимися колебаниями или без колебаний (апериодически).
Под действием сигнала управления щ золотник может занимать любые положения в пределах х3 < |хзтах|. При этом, согласно уравнению (6.47), на фазовой плоскости координата будет изменяться, а Х23 оставаться равной нулю.
Предположим, что золотник смещен от среднего положения на х3 или х32 (см. рис. 6.6, б). Эти смещения определяют точки 0 и О2 на кривой 3, в них су 0. При малом отклонении от точки 0 вправо или от точки О2 влево су < 0.
Если к тому же 6 = 0, то корнями уравнения (6.50) будут два равных по абсолютному значению числа, из которых одно положительное, а другое — отрицательное. Особую точку при таких корнях уравнения называют седлом. Через нее проходят сепаратрисы, разделяющие на фазовой плоскости области, которым соответствуют незатухающие (при 6 = 0) колебания золотника, и области неустойчивых равновесных положений золотника. Для смещений золотника от среднего положения в отрицательном направлении траектории, построенные в правой половине фазовой плоскости, зеркально отображаются на левую полуплоскость. На рис. 6.7 показаны сепаратрисы, иллюстрирующие возможность появления незатухающих колебаний золотника в окрестности его среднего положения и вблизи смещений, близких к хзтах.
![]() Рис. 6.7. Области незатухающих колебаний золотника на фазовой плоскости
Рис. 6.7. Области незатухающих колебаний золотника на фазовой плоскости
Условия, при которых возможны автоколебания золотника, определим с помощью критерия Бендиксона о существовании предельных циклов на фазовой плоскости. Согласно этому критерию, если в какой-то области фазовой плоскости выражение
Ад д
Дх дх2
Сохраняет постоянный знак, то предельный цикл не существует. Здесь /1 = /1(^1; х2) и /2 = /2(^1; х2) являются правыми частями уравнений, описывающих движение исследуемой системы на фазовой плоскости.
В нашем случае в соответствии с уравнениям (6.45) и
(6.46)
Л = /2 = Р(х) - Ьх2 + МО,
Поэтому д}/дх = 0; д/2/<9^2 = —Ь. Следовательно, автоколебания возможны при Ь < 0.
Чтобы исключить возможность возникновения автоколебаний, необходимо обеспечить во всем диапазоне перемещений золотника положительные значения су (см. рис. 6.6, б) и 6. Значения С/ > 0 достигаются, если сила пружины будет существенно больше гидродинамической силы, а 6 > 0 будет в отсутствие “отрицательного демпфирования” золотника.
Автоколебания в устройстве “сопло-заслонка”
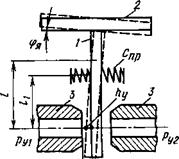
Автоколебания заслонки, управляющей расходом рабочей среды через сопло, также могут быть вызваны действием гидродинамических сил. Для анализа устойчивости составим математическую модель устройства, схема которого дана на рис. 6.8. Уравнение движения заслонки 1 вместе с якорем 2 электромеханического преобразователя запишем в виде
|
|
Где /я — момент инерции якоря заслонки; <ря — угол отклонения якоря от положения, принятого за нейтральное; Мэ — крутящий момент, создаваемый электромагнитными силами, действующими на якорь; Мд. я — демпфирующий якорь момент (см. формулу (5.77)); спр — жесткость пружин^ удерживающих заслонку в нейтральном положении, эквивалентна жесткости упругой трубки, если заслонка закреплена в ней, (см. рис. 5.8, 6); Ртд —гидродинамическая сила, действующая на заслонку при истечении рабочей среды через сопла 3; 1пр — 1 — 11.
|
|
Рис. 6.8. Схема сопла-заслонки для расчета автоколебаний
При малых углах поворота якоря допустимо считать, что
Hy = 1<ря. (6.52)
Гидродинамическая сила Ргп зависит от режима истечения рабочей среды через сопла. При малых зазорах hc поток среды может прилипать к торцу сопла, а при несколько больших значениях hc не соприкасаться с ним. Изменение режима истечения отражается на гидродинамической силе, определять которую с учетом возможной смены безотрывного и отрывного движения среды в зазоре между заслонкой и торцом сопла крайне сложно. Поэтому для анализа влияния гидродинамической силы на устойчивость положения заслонки представим эту силу функцией
Ргд = F(hy), (6.53)
Которая может быть нелинейной и неоднозначной. Такая функция не линеаризуема при переходе к малым отклонениям переменных, в связи с чем применим метод гармонической линеаризации. Вследствие того, что функция (6.53) может быть неоднозначной, усеченный в пределах первой гармоники ряд Фурье запишем в виде
F(hy) = F°(h°,ah) + q(h%,ah)ah sin ф+
+9l(^’abWcos^> (6.54)
Где ^0(/1у, ад) — постоянная составляющая гидродинамической силы; hy — смещение заслонки, относительно которого измерена амплитуда ад ее колебаний; 5(Лу, ад) и 51(Лу, ад) — коэффициенты гармонической линеаризации, вычисляемые по формулам для коэффициентов ряда Фурье.
С целью большей наглядности результатов анализа предположим, что при выбранном положении заслонки F°(hу, ад) = = 0. В этом случае коэффициенты гармонической линеаризации вычисляются по формулам
2тг
Q(ah) =----- / F(ah sin ф) sin ф<1ф-, (6.55)
Тга/, J 0
|
*4 1 о |
После замены функции (6.53) ее гармонически линеаризованным выражением (6.54) с учетом принятого выше допущения опишем гидродинамическую силу уравнением
|
<11 (ад) dh |
|
У |
|
Dt ’ |
|
Ргд — <l(ah)h у + |
|
|
Где hy = ад sina;^; ut = ф] ч{аь) и Ql(ah) являются функциями (6.55) и (6.56) от ад соответственно.
В основе метода гармонической линеаризации лежит предположение о наличии в исследуемой системе гармонических колебаний. Чтобы заслонка совершала такие колебания вместе с якорем, при Мэ = const характеристическое уравнение, полученное для дифференциального уравнения (6.51), в которое предварительно подставлена вместо Ргд правая часть уравнения (6.57), должно иметь мнимые корни. Выполнив указанные подстановки и учитывая соотношение (6.52), получим характеристическое уравнение
|
|
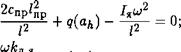 При А = уравнение (6.58) содержит вещественную и мнимую части, которые по отдельности должны быть равны нулю:
При А = уравнение (6.58) содержит вещественную и мнимую части, которые по отдельности должны быть равны нулю:
(6.59)
(6.60)
![]() Уравнение (6.59) позволяет найти
Уравнение (6.59) позволяет найти
(6.61)
А уравнение (6.60) — определить амплитуду ад. Подставив полученное значение ад в выражение для <?(ад), можно по фор
Муле (6.61) вычислить частоту колебаний заслонки с якорем. Если эти колебания устойчивы, то они являются автоколебаниями. Для проверки устойчивости колебаний в уравнение (6.60) подставим значение ад с положительным и отрицательным приращениями Лад. Если при ад + Дад левая часть уравнения (6.60) получится больше нуля, а при ад - Дад меньше нуля, то колебания будут устойчивыми, т. е. имеют место автоколебания с вычисленными указанным выше образом частотой и амплитудой.
Проведенный анализ показывает, что причиной автоколебаний в устройстве сопло-заслонка могут быть режимы течения, при которых гидродинамическая сила создает “отрицательное демпфирование” заслонки. Однако в данном случае природа явления отличается от “отрицательного демпфирования” золотника, рассмотренного выше.
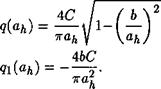 Для иллюстрации возможных особенностей гидродинамической силы, действующей на заслонку, предположим, что функция (6.53) имеет график, изображенный на рис. 6.9. При таком графике
Для иллюстрации возможных особенностей гидродинамической силы, действующей на заслонку, предположим, что функция (6.53) имеет график, изображенный на рис. 6.9. При таком графике
(6.62)
(6.63)
Подставив 91 (ад) из формулы (6.63) в уравнение (6.60), нетрудно найти ад и убедиться, что возникающие с такой амплитудой колебания будут автоколебаниями.
|
|
С
|
В |
![]()
|
В |
![]()
![]() Рис. 6.9. Возможная зависимость гидродинамической силы от перемещения заслонки при расчете автоколебаний
Рис. 6.9. Возможная зависимость гидродинамической силы от перемещения заслонки при расчете автоколебаний
Неустойчивость клапанов в системе с распределенными параметрами
При анализе причин возникновения автоколебаний золотников и заслонки эти устройства были представлены как сравнительно простые нелинейные системы, выделенные из более сложных гидро - и пневмосистем. Однако вследствие образования в последних системах внутренних динамических контуров на устойчивость устройств, управляющих потоками рабочих сред, наряду с рассмотренными ранее могут влиять и другие факторы. Для примера рассмотрим систему клапан — трубопровод, схема которой дана на рис. 6.10. В этой системе на конце трубопровода длиной I установлен клапан, нагруженный пружиной с жесткостью спр. Рабочая среда поступает в трубопровод из аккумулятора А. Используя уравнения (4.23) и (4.24), составим модель системы с учетом распределенности параметров по длине трубопровода. Выполнив при нулевых начальных условиях одномерное преобразование по Лапласу этих уравнений, получим
|
Втр = ~зр(з)’ (6-65) где р(з), ^(з), тон(«$) — изображения по Лапласу соответственно ВеЛИЧИН р, V, Т()н-
Рис. 6.10. Система клапан-трубопровод |
Изображение tqh(s) нестационарного касательного напряжения в месте контакта рабочей среды и стенки трубопровода определим с помощью передаточной функции
Wrv(s) = (6.66)
V{s)
|
Dp(s) dx |
|
2 Wrv(s) |
|
Ps + |
|
Го |
|
V(s) = - |
|
|
Продифференцировав уравнение (6.67) по I и применив уравнение (6.65), приведем систему из двух дифференциальных уравнений к одному уравнению
(6.68)
Где
|
2Wrv(s)] |
|
Ps + |
|
В |
|
Го |
|
Тр |
|
Т = ±1 |
|
|
Величина t?(s) в изображениях по Лапласу характеризует распространение возмущений в рабочей среде вдоль трубопровода, поэтому ее называют операторным коэффициентом распространения. Она связана с операторным волновым сопротивлением ZB(s) соотношением
J3Xpi?(s) = sZB(s). (6.70)
Уравнение (6.68) имеет решение
Р(з, х) = Cie*W* + C2e-*W* (6.71)
Постоянные С и С*2 определяются граничными условиями. Пусть при х = 0 (см. рис. 6.10, сечение 1-1)
P(a,*) = pi(в,0); (6.72)
|
(6.73) |
![]() Dp(s, x) ^(s)5-rp
Dp(s, x) ^(s)5-rp
Dx в
После подстановки постоянных С и Сг, вычисленных с помощью соотношений (6.72) и (6.73), решение (6.71) принимает вид
Р(з, х) = -
|
’)• |
![]()
|
(6.74) |
2s
|
Ії(з)ВтірУі(з, 0) |
![]()
|
ВЬ[0(д)а:]. (6.75) |
![]()
|
Переходя в (6.74) к гиперболическим функциям, получаем |
![]() Р(з, X) = Рі(з, 0) сЬ[і?(5)ж] -
Р(з, X) = Рі(з, 0) сЬ[і?(5)ж] -
SHAPE \* MERGEFORMAT ![]()
Решив систему уравнений (6.64) и (6.65) относительно г;(5, ж), найдем
|
|
Подставив в уравнения (6.75) и (6.76) х = I и выполнив затем несложные операции, определим передаточную функцию
|
1 |
|
8Ь[і?(й)/] + сЬ[$(з)/] |
|
Р2(Д»0 _ ________________ Рі(*,0) Зв. л(а) Ад |
|
|
Где
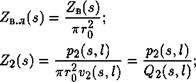 (6.78)
(6.78)
(6.79)
^в. л(з) — волновое сопротивление линии (трубопровода); $2(5>0 — изображение расхода в сечении 2-2 (см. рис. 6.10); ^г(5) — операторное сопротивление (импеданс) нагрузки, подключенной в сечении 2-2 к трубопроводу.
![]() Передаточной функции (6.77) соответствует изображенная на рис. 6.11 структурная схема. Устойчивость такой системы с распределенными параметрами можно проверить по критерию Найквиста, предварительно получив ^(з). Ддя это" го согласно соотношению (6.79) необходимо найти связь между изображениями рг(5) и $2(5)- Если расход через сечение 2-2 (см. рис. 6.10) регулирует клапан, то изображение $2(5) можно найти после линеаризации функции
Передаточной функции (6.77) соответствует изображенная на рис. 6.11 структурная схема. Устойчивость такой системы с распределенными параметрами можно проверить по критерию Найквиста, предварительно получив ^(з). Ддя это" го согласно соотношению (6.79) необходимо найти связь между изображениями рг(5) и $2(5)- Если расход через сечение 2-2 (см. рис. 6.10) регулирует клапан, то изображение $2(5) можно найти после линеаризации функции
(6.80)
Здесь фкл — расход среды, пропускаемой клапаном из трубопровода на слив; /хкл — коэффициент расхода клапана; гікл,
|
|
Рв(*)
|
|
Рис. 6.11. Структурная схема системы клапан - трубопровод с распределенными параметрами
#кл — диаметр клапана и его перемещение; ркл — перепад давления, при котором происходит истечение среды через клапан; р — плотность среды.
В малых отклонениях переменных от своих установившихся значений, линеаризовав функцию (6.80), имеем
|
|
|
$2 = Кдхх + К<2РР2, |
|
(6.81) |
|
^КлТГ С? к Л £ к л |
#КЛ) Ркл? Р-
Чтобы найти изображение рг(5)> запишем дополнительно уравнение движения клапана в малых отклонениях переменных
|
|
Где гакл — масса клапана; £д — коэффициент демпфирования клапана; спр — жесткость пружины, нагружающей клапан; стд — коэффициент линеаризованной зависимости гидродинамической силы от перемещения клапана (жесткость “гидродинамической пружины”); 5КЛ = ^кл/4 — площадь клапана.
После преобразования по Лапласу при нулевых начальных условиях уравнений (6.81) и (6.82) найдем
Р2(3) _________ гпклв2 + +____________ СПр + сгд ^
$2(5) + ка$ + Спр "I" сгд)
Необходимую для применения критерия Найквиста АФЧХ ИЛс(У^)разомкнутого контура системы определим, подставив в = Зш в передаточные функции звеньев, показанных на рис. 6.11. В результате имеем
Комплексные выражения в формуле (6.84) для вычисления ]¥с^и) определим следующим образом. Согласно соотношениям (6.70) и (6.78)
7Г ГдЗ
Поэтому
*„1*0 = (6.85)
В комплексном выражении коэффициента распространения выделим действительную и мнимую части:
‘<и) = 6 + 1е, (6.86)
Где 6 — коэффициент затухания, который характеризует уменьшение амплитуды давления или скорости среды в волне, распространяющейся вдоль трубопровода; е — коэффициент фазы, связанный с фазовой скоростью волны соотношением сл = и/е.
С учетом нестационарного сопротивления трения эти коэффициенты можно вычислить по формулам
4аел1/ I ро
Г Г
Втр — модуль объемной упругости среды, находящейся в упругом трубопроводе, радиус проходного сечения которого равен го] і/ — кинематическая вязкость среды.
Комплексную величину Z2(ju>)) подставив э = їй ъ формулу (6.83), найдем в виде
|
СПр “Ь сгд — 'М'клШ2 +
|
С помощью формул (6.84)-(6.89) можно построить АФ - ЧХ разомкнутого контура системы или ЛАХ и ЛФХ
Этого контура. По ним описанным в § 6.1 методом на основании критерия Найквиста проверяется устойчивость системы трубопровод-клапан.
Для анализа влияния гидродинамической силы на устойчивость клапана упростим математическую модель системы, предположив, что можно пренебречь сопротивлением трения трубопровода (течение маловязкой среды) и для малых х^л принять Кцр — 0. При таких допущениях АФЧХ (6.84) разомкнутого контура системы приведем к виду
|
|
Где
|
Кц — &д/™кл- |
В случае АФЧХ (6.90) система трубопровод - клапан может быть неустойчива, если при какой-то частоте и значение а^ТУсС?^) станет равным —7Г при значении модуля ¥с^и) больше единицы. Указанные условия имеют место при
(6.91)
Из соотношения (6.91) следует, что при неизменных параметрах клапана устойчивость системы зависит от длины трубопровода. При одной и той же длине трубопровода причиной неустойчивости системы может быть изменение частоты а;о, поскольку изменяется коэффициент сгд гидродинамической силы, действующей на клапан. В свою очередь сгд зависит от режима истечения среды из-под клапана. Если происходит смена отрывного обтекания клапана безотрывным, то возможно возникновение неустойчивости системы, сопровождающееся автоколебаниями клапана и среды в трубопроводе.