СОВРЕМЕННЫЕ СИСТЕМЫ УПРАВЛЕНИЯ

Выбор параметров с помощью корневого годографа

Изначально метод корневого годографа был разработан как средство определения траекто­рий корней характеристического уравнения системы при изменении её коэффициента уси­ления К от 0 до со. Однако, как мы видели, с помощью этого метода можно исследовать и влияние изменения других параметров системы. Метод корневого годографа основан на использовании характеристического уравнения системы вида

1 + F(s) = 0 . (7.65)

В данном случае мы можем воспользоваться уже известными приёмами. Однако воз­никает вопрос: а как быть, если надо исследовать влияние двух варьируемых парамет­ров — скажем, а и Р? Обычный метод корневого годографа предполагает, что варьирует­ся один параметр системы. Но этот метод тем и хорош, что позволяет исследовать влия­ние двух и более параметров. Поэтому метод корневого годографа можно использовать как метод выбора параметров системы.

Характеристическое уравнение динамической системы в общем случае имеет вид:

aj1 + an_lsn~i + ... + + а0 = 0. (7.66)

Следовательно, мы можем исследовать влияние коэффициента аь приведя это уравнение к виду:

1+---------------------- ^--------- 5-------- =0. (7.67)

ansn + an_xsn +...+a2s~ +а0

Если интересующий нас параметр а не входит явно в это уравнение как коэффициент, то мы можем выделить его в следующем виде:

ans" + an_, s'7-1 +.. ,+(an_cj — a )j"~<y + asn~cl +.. .+а, s + а0 =0. (7.68)

Например, для системы третьего порядка это может выглядеть так:

я3 + (3 + a)s2 + 3s + 6 = 0 . (7.69)

Для того чтобы исследовать влияние параметра а, мы выделим его и произведём следую­щие действия:

53 + 3s2 + as2 + Is + 6 = 0; (7.70)

1 + ^------------------ =0. (7.71)

s + 3s" + 3j + 6

Далее, чтобы исследовать влияние двух параметров, нам потребуется дважды повторить все действия, связанные с построением корневого годографа. Так, если в характеристиче­ское уравнение входят два варьируемых параметра а и р, то мы имеем: ansn ^■fl„_1i”'1+...+(fl^ї-а)s"", + as"~4 +...+(ап_г - Р)/'~г +p. s"-r+...+a1.s + a0 =0

(7.72)

Таким образом, два параметра оказываются выделенными, и можно будет исследовать влия­ние р после того, как будет исследовано влияние параметра a. Например, предположим, что характеристическое уравнение системы третьего порядка содержит два параметра, а и Р:

В данном случае аир являются коэффициентами характеристического уравнения. Влия­ние изменения р от 0 до оо можно определить по уравнению корневого годографа:

1+ —^------------ =0.---------------------------------------------- (7.74)

s +s~ + а

Заметим, что в (7.74) знаменатель представляет собой характеристический полином систе­мы при р = 0. Поэтому сначала можно оценить влияние параметра а с помощью уравнения

j3 + s2 + а = 0,

переписав его в виде

(7.75)

что эквивалентно заданию р = 0 в уравнении (7.73). Далее, исследовав влияние а, выбира­ется конкретное значение этого параметра, которое подставляется в (7.74), после чего оце­нивается влияние р. В этой двухшаговой процедуре мы сначала строим корневой годограф, считая варьируемым параметр а и выбираем его значение, соответствующее приемлемому расположению корней. Затем строим корневой годограф, считая варьируемым параметр Р; при этом полюсы в (7.74) определяются корнями, найденными на основании уравнения

(7.75) . Данный метод, к сожалению, имеет одно ограничение, а именно — не всегда можно записать характеристическое уравнение, в которое варьируемый параметр входил бы ли­нейно.

Чтобы наглядно проиллюстрировать описанный метод, построим корневой годограф по уравнению (7.73), проварьировав сначала параметр а, а затем р. Траектории корней для уравнения (7.75) при изменении а показаны на рис. 7.18 (о); там же отмечено положе­ние корней, соответствующее двум значениям параметра а. Если выбрать а = сс,, то корни уравнения (7.75) становятся полюсами (7.74). Далее в уравнении (7.74) можно проварьи - ровать параметр р и по корневому годографу на рис. 7.18 (б) на основании желаемого рас­положения корней выбрать конкретное значение р.

Рассмотрим ещё один пример, иллюстрирующий применение метода корневого го­дографа для выбора параметров системы.

-X ►

а, р

«)

Рис. 7.18. Траектории корней при изменении параметров аир: (а) корневой годограф при изменении а;

(б) корневой годограф для а = сц и изменения р

Пример 7.5. Управление положением наконечника сварочного узла

При сборке автомобильных кузовов требуется точное позиционирование наконечника свароч­ного узла. Для этого замкнутая система управления должна удовлетворять следующим требо­ваниям:

1. Установившаяся ошибка при линейном входном сигнале не более 35% по отношению к ско­рости изменения входного сигнала.

2. Коэффициент затухания, соответствующий доминирующим корням, С, > 0,707.

Рис. 7.19

Структурная схема

G(s)

K,s

3. Время установления (по критерию 2% от конечного значения) — не более 3 с. Структура системы управления приведена на рис. 7.19, а выбору подлежат коэффициенты К, и К2. Установившуюся ошибку можно представить в виде:

е„ = lime(f) = limj£(s) = ^ , (7.76)

/->« ,v-»o.«->о 1+G2(s)

где G2(s) = G(s)/( 1 + G(s)H(s)). Таким образом, ограничение на установившуюся ошибку при­водит к соотношению:

= 2 +К{К2 ^

Щ

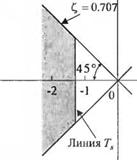
У читывая данное неравенство, мы выберем малое значение К2. Заданный коэффициент затуха­ния требует, чтобы корни характеристического уравнения замкнутой системы находились ниже линии под углом 45° в левой половине s'-плоскости. Время установления можно выра­зить через действительную часть доминирующих корней:

Т,=-<Зс. (7.78)

о

Отсюда следует неравенство о > 4/3; вместе с ограничением на (, это позволяет определить область расположения корней на ^-плоскости. Эта область отмечена темным цветом на рис. 7.20. Параметры, подлежащие выбору, можно обозначить как а = К, и Р = К2 К}. Тогда характеристическое уравнение примет вид:

1 + GH(s) = .r + 2y + Ps+a = 0. (7.79)

Полагая р = 0 и считая варьируемым параметр a = К,, получим

уравнение корневого годографа:

1+—-— = 0. (7.80)

s(s + 2)

На корневом годографе, изображённом на рис. 7.21 (о), отмечено положение корней при Kt = a = 20. Далее мы исследуем положе­ние корней при Р = 20А2, для чего построим корневой годограф по уравнению:

1+ —z——--- = 0, (7.81)

s + 2s + a

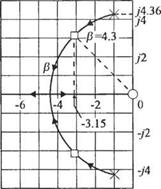
причем в данном случае полюсы являются корнями на годографе рис. 7.21 (а). Результат по­строения второго корневого годографа представлен нарис. 7.21 (б), а корни, соответствующие £ = 0,707, получаются при Р = 4,3 = 20Х2, откуда К2 = 0,215.

Действительная часть этих корней а = 3,15 и, следовательно, время установления (по крите­рию 2 % от конечного значения) равно 1,27 с, что значительно меньше заданного ограничения в 3 с.

а) б)

Метод корневого годографа можно распространить и на случай, когда имеется более двух варьируемых параметров. При этом просто увеличивается число этапов, подобных рассмотренным выше. Более того, можно построить семейство траекторий корней при од­новременном изменении двух параметров. Например, исследуем влияние изменения па­раметров а и Р, входящих в следующее характеристическое уравнение:

л3 + 3s2 + 2s + Ps + а = 0. (7.82)

Уравнение корневого годографа в зависимости от а (при Р = 0) имеет вид:

1 + = 0. (7.83)

5(5+ 1)(5+2)

В свою очередь, корневой годограф в зависимости от р имеет уравнение

1+- Р = 0. (7.84)

s +3s" +2j+ct

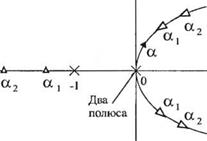
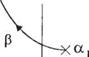
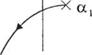
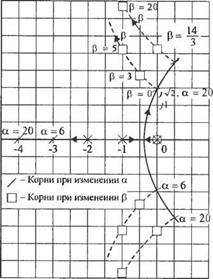
Корневой годограф, соответствующий уравнению (7.83), как функция а, изображён сплошными линиями на рис. 7.22. Корни на этом годографе, обозначенные чёрточками, становятся полюсами для уравнения (7.84). Построенный по этому уравнению годограф изображён на рис. 7.22 пунктирными линиями, а на ветвях, соответствующих некоторым значениям а, отмечено положение корней при различных р. Семейство таких траекторий, часто называемое линиями корней, позволяет оценить влияние параметров а и р на корни характеристического уравнения системы.

Рис. 7.22

Корневой годограф для случая двух варьируемых параметров