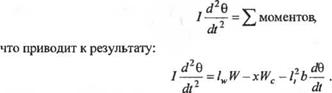СОВРЕМЕННЫЕ СИСТЕМЫ УПРАВЛЕНИЯ

Пример анализа и синтеза системы управления с помощью метода корневого годографа

Анализ и синтез системы управления можно выполнить с помощью преобразования Лап­ласа, сигнального графа, 5-плоскости и метода корневого годографа. В данном разделе мы рассмотрим конкретную систему управления и выберем надлежащие значения её парамет­ров, воспользовавшись методом корневого годографа.

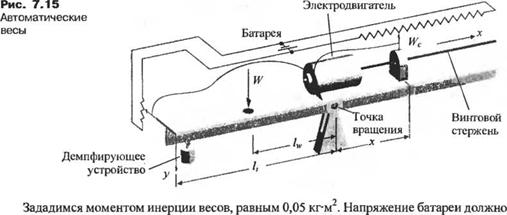
На рис. 7.15 изображены автоматически уравновешивающиеся весы, в которых взве­шивание предмета производится за счёт использования цепи электрической обратной связи. Весы изображены находящимися в положении равновесия, где х — смещение про­тивовеса Wc при отсутствии груза. Взвешиваемый груз W помещается на расстоянии 5 см от оси вращения, а расстояние от этой оси до демпфирующего устройства /, = 20 см. Требуется выполнить следующее:

1. Выбрать параметры системы и задать требования к её качеству.

2. Получить модель системы в виде сигнального графа.

3. На основании корневого годографа выбрать значение параметра К.

4. Определить доминирующую составляющую реакции системы.

быть достаточным, чтобы обеспечить приемлемое значение коэффициента передачи дат­чика положения, поэтому выберем Еъь = 24 В. Будем считать, что винтовой стержень со­здаёт смещение противовеса с коэффициентом пропорциональности 20 об/см, а длина по­тенциометра, играющего роль датчика положения х, равна 6 см. Точность взвешивания должна быть высокой, поэтому для измерения координаты у выберем вспомогательный потенциометр длиной 0,5 см. Демпфирующее устройство выберем с коэффициентом вяз­кого трения b = 1(Н/3 кг/(м/с). Наконец, противовес Wc выберем так, чтобы он был спосо­бен уравновешивать любой груз W в ожидаемом диапазоне. Все выбранные параметры системы представлены в табл. 7.4.

Требования к качеству системы. Желательно, чтобы система автоматического взвешивания обладала высоким быстродействием и имела малую установившуюся ошиб­ку. Поэтому мы потребуем, чтобы система относилась, по крайней мере, к типу 1, при ко­тором ошибка измерения будет равна нулю. Допускается колебательный характер реак­ции системы на ступенчатое изменение веса W, поэтому зададимся относительным коэф­фициентом затухания £ = 0,5. Потребуем также, чтобы после помещения на весы груза время установления (по критерию 2 % от конечного значения) было не более 2 с. Эти основные требования сведены в табл. 7.5.

Таблица 7.5. Требования к качеству системы

Установившееся ошибка Кр = оо, еЛЛ = 0 при ступенчатом входном воздействии

Колебательный характер реакции системы £ = 0,5

Время установления (по критерию 2%) Менее 2 с_______________________________

Модель электромеханической системы взвешивания можно получить на основании уравнений движения. При малых отклонениях от положения равновесия угол отклонения 0 можно представить как

0*^-.

h

Движение коромысла весов можно описать уравнением

(7-55)

Vm(s) 5(т5+1)’

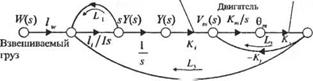
где т будем считать пренебрежимо малой в сравнении с постоянными времени системы, а 0„, — угол поворота вала двигателя. Сигнальный граф, отражающий уравнения (7.55)-{7.57), изображён на рис. 7.16. Исследуя прямой путь от W к Да), мы можем видеть, что система относится к типу 1 за счёт наличия интегратора перед У(л). Следовательно, установившаяся ошибка системы будет равна нулю.

Передаточную функцию замкнутой системы найдём с помощью формулы Мейсона:

где числитель есть коэффициент передачи пути от W к X, второй член в знаменателе соот­ветствует контуру і,, третий — контуру Li, четвёртый — контуру JL3, а пятый образован двумя некасающимися контурами Lx L2- Окончательно передаточная функция замкнутой системы имеет вид:

lwhK, KmKs

W(s) sUs + lfb)(s+KmKsKf)+WcKmKsK, ll

Отсюда следует, что коэффициент передачи системы в установившемся режиме равен

если = | W/s. Чтобы построить корневой годограф в зависимости от постоянной элект­

родвигателя Кт, подставим в характеристическое уравнение, т. е. в знаменатель выражения (7.59), значения выбранных параметров и получим:

Ф+8ТЗ)Ь+^-| + ^^=0. (7.61)

Л 10л) 10л

Чтобы привести это уравнение к виду, удобному для построения корневого годографа, прежде всего выделим в нём члены, содержащие Кт:

д2(д+8л/3) + д(д+&^/3)^!-+ =0.

10л 10л

Далее приведём (7.62) к виду уравнения корневого годографа:

11 кр(=) -11(Кт /10я)№+8^з)+96] _ s2(s+sS)

(K„,/10n)(s+ 6,93 + 76,93 )(^+6,93-76,93)

(7.62)

(7.63)

s2(s+ 8л/3)

Корневой годограф в функции от параметра Кт изображен на рис. 7.17. При С, = 0,5 домини­рующие корни занимают положение, указанное на рисунке, если К=25,3= KJ Юл. Отсюда следует, что постоянная электродвигателя, как часть общего коэффициента передачи сис­темы, должна быть равна