СОВРЕМЕННЫЕ СИСТЕМЫ УПРАВЛЕНИЯ

Требования к качеству системы в частотной области

Мы постоянно должны задавать себе вопрос: какая связь существует между частотными характеристиками системы и ожидаемым видом её переходной характеристики? Другими словами, если задан набор требований к поведению системы во временной области (к виду её переходной характеристики), то каким требованиям должны отвечать частотные харак­теристики этой системы? Для простой системы второго порядка мы уже получили ответ на

этот вопрос, рассмотрев такие показатели качества во временной области, как перерегулирование, вре­мя установления и ряд других, включая интеграль­ные оценки. Замкнутая система второго порядка, изображена на рис. 8.24, имеет передаточную функ­цию

7

ҐІЛ"

T(s) =

s2 +2^Ю()5 + (й2

Рис. 8.24. Замкнутая система второго порядка

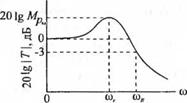
Амплитудно-частотная характеристика этой системы выглядит так, как показано на рис. 8.25. Поскольку система имеет второй порядок, то её коэффициент затухания одно­значно связан с максимумом амплитудной характеристики MR, который имеет место на частоте саг (см. рис. 8.25).

Максимальное значение амплитудно-частотной характеристики, Мр, имеет место на резонансной частоте сог.

Полоса пропускания ыи определяет способность системы правильно воспроизводить входной сигнал.

Полоса пропускания определяется частотой юй, на которой амплитудно-частот­ная характеристика системы уменьшается на 3 дБ относительно её значения на низких частотах.

Можно установить связь между резонансной час­тотой и полосой пропускания системы и скоростью на­растания её переходной характеристики. Так, при уве­личении полосы пропускания сол будет уменьшаться время нарастания переходной характеристики. Кроме того, относительное перерегулирование переходной характеристики можно связать с показателем М р, ко­торый в свою очередь определяется коэффициентом затухания Кривые на рис. 8.11 связывают резонанс­ную частоту и максимум амплитудно-частотной ха­рактеристики с коэффициентом затухания системы второго порядка. А с помощью рис. 5.8 или путём непосредственных вычислений по вы­ражению (5.15) можно оценить величину относительного перерегулирования реакции си­стемы на ступенчатый входной сигнал. Поэтому легко установить, что при увеличении резонансного пика Мр будет возрастать и величина перерегулирования. Таким образом, показатель Мр в определённой степени является оценкой устойчивости системы.

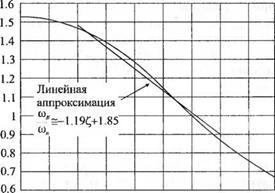
Полоса пропускания системы <ли лишь приблизительно может быть связана с собст­венной частотой колебаний со,,. На рис. 8.26 приведена зависимость отношения со^/ю,, от коэффициента затухания £ для системы второго порядка с передаточной функцией (8.46). Реакция такой системы на единичный ступенчатый сигнал определяется выражением

y{t)=+Ве~^' cos(co, f + e> (8.47)

Отсюда ясно, что при С, = const, чем больше значение со,,, тем быстрее переходная ха­рактеристика достигает установившегося значения. Таким образом, желательно, чтобы частотные характеристики системы удовлетворяли следующим требованиям:

С

1. Максимум амплитудно-частотной характеристики должен быть достаточно малым, например, Мр < 1,5.

2. Полоса пропускания системы должна быть достаточно большой, чтобы постоян­ную времени х - 1/^са„ можно было считать малой.

Насколько эти требования в действительности будут соответствовать желаемым по­казателям переходной характеристики, зависит от того, удастся ли произвольную систему аппроксимировать моделью второго порядка, выделив в её передаточной функции T(s) пару доминирующих полюсов. Эта проблема обсуждалась ранее в разделе 7.3. Если вид частотных характеристик в основном определяется парой комплексных полюсов, то об­суждаемая в данном разделе связь между частотными и временными характеристиками будет вполне обоснованной. К счастью, на практике для большей части систем управле­ния высказанные соображения действительно являются справедливыми.

Требования к величине установившейся ошибки также можно описать в терминах частотных характеристик замкнутой системы. Как мы выяснили в разделе 5.4, установив­шуюся ошибку в случае входного сигнала заданного вида можно связать с коэффициен­том усиления разомкнутой системы и числом интеграторов, входящих в её передаточную функцию. Например, для системы, изображённой на рис. 8.24, установившаяся ошибка при линейном входном сигнале определяется коэффициентом ошибки по скорости, Kv:

lim е(0 = -7~ ,

/—>00 К

V

где А - скорость изменения входного сигнала. Для системы на рис. 8.24 коэффициент ошибки по скорости равен

Выделив в передаточной функции G(s) постоянную времени, её можно представить в виде

а>„/2С Ку

(8.49)

s(sl 2^ю() +1) s(xs +1)

откуда видно, что для данной системы типа 1 коэффициентом усиления является Кг. На­пример, вернувшись к примеру из раздела 8.3, напомним, что мы имели дело с системой типа 1, передаточная функция которой

СО*)------------------------------------------------------------------------ (8.50,

7'со(1+у'сот, )(1 + j0,6u-и~ )

где и = со/со(,. Следовательно, в данном случае Kv = 5. В общем случае, если передаточную функцию разомкнутой системы записать в виде

м

А'Па+уит,)

СО)=------------------------------------- ,--------------------------------- (8.51)

(Ja)Nfl(l+j<04)

k=1

то она относится к типу N, и установившаяся ошибка определяется коэффициентом К. Так, система типа 0 имеет в разомкнутом состоянии передаточную функцию

С(» = ~ . * . , (8-52)

(1+усот, )(1+у(0Т2 )

и коэффициент ошибки по положению К = К определяет вид диаграммы Боде в области низких частот.

Аналогично, для системы типа 1 низкочастотный участок амплитудной характери­стики на диаграмме Боде определяется коэффициентом К = Kv. Действительно, ограни­чившись в выражении (8.50) только коэффициентом усиления и полюсом в начале коор­динат, мы получим:

С0'ш) = —= —, со < 1/х,. (8.53)

j со j со

Отсюда ясно, что коэффициент Kv численно равен частоте, при которой продолжение низ­кочастотного участка амплитудной характеристики пересекает уровень 0 дБ. Например, на рис. 8.20 продолжение низкочастотной асимптоты пересекает уровень 0 дБ при со = 5, как и следовало ожидать.

Таким образом, частотные характеристики позволяют достаточно адекватно оцени­вать качество системы, и при наличии определённых навыков они могут служить очень полезным инструментом анализа и синтеза систем управления.