СОВРЕМЕННЫЕ СИСТЕМЫ УПРАВЛЕНИЯ
Установившаяся ошибка систем управления с обратной связью
|
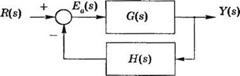
Рис. 5.18. Замкнутая система управления |
Одним из основных мотивов использования обратной связи, несмотря на усложнение системы и неизбежные издержки, является возможность уменьшения установившейся ошибки. Как было показано в разд. 4.5, в устойчивой замкнутой системе установившаяся ошибка на несколько порядков меньше, чем аналогичный показатель в разо-
мкнутой системе. Рассмотрим замкнутую систему, изображенную на рис. 5.18. Сигнал, по которому можно судить об ошибке системы, обозначен через Ea(s). Однако действительная ошибка характеризуется выражением E(s) = R(s) - У(і). Тогда
E(s) = R(s)--
1+ GH(s) 1+ GH(s)
Ошибка системы совпадает с сигналом Ea(s) при H(s) = 1. В этом случае
и установившаяся ошибка определяется выражением
|
(5.23) |
е5ї = lim e(t) = lim _
(-»«, a_>o 1 + G(s)
Полезно определить установившуюся ошибку системы в случае единичной обратной связи, H(s) = 1, для трех типовых тестовых входных сигналов.
Ступенчатый входной сигнал. При ступенчатом входном сигнале амплитуды А установившаяся ошибка равна
.. s(A/s) А
e..v = lim------------ =------------ ,
*->о 1 + С(л) 1+G(0)
т. е. она определяется передаточной функцией разомкнутой системы G(s). Последняя в общем случае записывается в виде
м
|
Рк) |
К П (■*+*/)
|
Таким образом, значение G(.s) при s —» 0 зависит от Л', т. е. количества содержащихся в разомкнутой системе интеграторов. Если N > 0 , то G(0) = да и установившаяся ошибка равна нулю. Часто используют термин тип системы, который просто равен количеству интеграторов N. Так, для системы типа 0 (7V = 0 ) установившаяся ошибка равна А А |
|
(5.25) |
|
е,, =- |
|
м о Кгь/Пл |
|
1+G(0) |
|
1+ |
|
i=i |
|
*=i |
|
Константа G(0), обозначаемая через Кр, называется коэффициентом ошибки по положению и определяется как |
|
Кр = limG(s). |
|
л'—>0 |
|
Таким образом, установившаяся ошибка при отработке ступенчатого воздействия с амплитудой А определяется выражением |
|
(5.26) |
|
1+К, |
|
Если система содержит один или более интеграторов, т. е. N > 1, то при единичном ступенчатом воздействии установившаяся ошибка равна нулю, т. к. |
|
As‘ |
|
А |
|
= lim |
|
= 0. (5.27) |
|
= lim- |
|
1+ (АГП zt / sN П Pk ) Л"[3]° sN + (*П z,1П Pk ) Линейный входной сигнал. Установившаяся ошибка в случае линейного входного сигнала (изменяющегося с постоянной скоростью А) определяется выражением: |
|
. s(A/s2) er, = lim-------------- = lim- |
|
А |
|
А |
|
(5.28) д—>о 1+G(s) - v~>o s+sG(s) *->о SG(s) Напомним, что установившаяся ошибка зависит от количества интеграторов, N. Для системы типа «ноль» N = 0, и установившаяся ошибка равна бесконечности. Для системы типа «один» N = 1, и ошибка А е,< = lim |
|
= lim- |
|
з{[кЦ (s+ z,)] / [sf| (s+ pk )]}’ |
|
или |
|
A |
|
A |
(5.29)
*Гbi'YlPk Kv ’
где Kv носит название коэффициента ошибки по скорости. Этот коэффициент вычисляется по выражению
Kv =limsG(s)i
v-»0
Если передаточная функция включает в себя два или более интеграторов, N > 2, то установившаяся ошибка равна нулю. При N = 1 установившаяся ошибка отлична от нуля, но скорость изменения выходной переменной равна скорости входного сигнала (см. рис. 5.20).
Квадратичный входной сигнал. Если на вход системы поступает сигнал r(t) = Ar/2, то установившаяся ошибка имеет вид:
.. 5(Л/5Л)
|
(5.30) |
= lim— = Iim-
.'->о 1+GC?) -'->о s^G(s)
При наличии одного интегратора установившаяся ошибка равна бесконечности; при двух интеграторах, N = 2, мы получим
(5.31)
где Ка — коэффициент ошибки по ускорению, определяемый выражением
Ка =lims2G(s).
А’—>0
Если количество интеграторов N> 3, то установившаяся ошибка равна нулю.
Системы управления часто характеризуют их типом и коэффициентами ошибки Кр, Kv и Ка. Установившиеся ошибки для трех входных сигналов в зависимости от типа системы приведены в табл. 5.5. Пользу от использования коэффициентов ошибки мы проиллюстрируем на простом примере.
|
Таблица 5.5. Установившиеся ошибки
|
Пример 5.3. Управление рулевым механизмом подвижного робота
Тяжело больной человек может воспользоваться подвижным роботом в качестве помощника или обслуживающего устройства. Система управления рулевым механизмом такого робота представлена в виде структурной схемы на рис. 5.19.
Регулятор имеет передаточную функцию
|
-R(s) |
о
Желаемое направление движения
|
Динамика робота |
||
|
Регулятор |
||
|
К |
||
|
Gj(s) |
G<S>- ts+l |
У(3)
Действительное
направление
движения
Рис. 5.19. Структурная схема системы управления рулевым механизмом
подвижного робота
При К2 = 0 и Gj(s) = Кх установившаяся ошибка системы при ступенчатом входном сигнале равна
е„ = —— . (5.33)
1 +Кр
где Кр = КК{. Если К-у 0, то мы имеем систему типа 1, т. е.
S
и установившаяся ошибка при ступенчатом входном сигнале равна нулю.
Если управляющий входной сигнал является линейным, то установившаяся ошибка
е =-^-. (5.34)
где
Kv = lim. vG|(sX7(.s-) = К2К.
|
|
s—>0
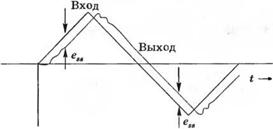
На рис. 5.20 изображена реакция си - y(t) стемы на периодический сигнал треугольной формы при G](s) = (KjS +
+ K2)/s. На переходной характеристике отчетливо прослеживается появление установившейся ошибки, которая может не иметь существенного значения, если Kv достаточно велико. Заметим, что хотя в установившемся режиме ошибка отлична от нуля, но выходной сигнал изменя - Рис. 5.20. Реакция системы на колебания ется с заданной скоростью. треугольной формы
Коэффициенты ошибки Кр, Kv и Ки характеризуют способность системы управления уменьшать или устранять установившуюся ошибку. Поэтому они используются как количественные показатели качества системы в установившемся режиме. Проектировщик определяет коэффициенты ошибки для конкретной системы и пытается найти способы их увеличения, сохраняя в то же время приемлемое качество переходной характеристики. В примере с системой управления рулевым механизмом подвижного робота желательно увеличивать произведение КК2, чтобы увеличить Kv и тем самым уменьшить установившуюся ошибку. Однако увеличение КК2 приводит к одновременному уменьшению коэффициента затухания £ и, следовательно, к более колебательному характеру реакции системы на ступенчатое входной воздействие. Поэтому в данном случае должен быть найден разумный компромисс между значениями параметров Kv и С,.