СОВРЕМЕННЫЕ СИСТЕМЫ УПРАВЛЕНИЯ
Синтез системы управления роботом
Понятие воспроизводства роботов объяснить можно довольно просто. Идея заключается в том, что роботы воспроизводят себе подобных и создают завод, который автоматически выпускает продукцию в виде роботов. Процесс воспроизводства роботов изображён на рис. 7.33. Чтобы создать быстродействующую и высокоточную систему управления роботом, важно обеспечить жёсткость и в то же время малую массу руки робота.
|
|
|
Рис. 7.33 Процесс воспроизводства роботов |
Система управления движением руки робота должна удовлетворять следующим требованиям: (1) время установления (по критерию 2%) должно быть не более 2 с, (2) перерегулирование при ступенчатом входном сигнале допускается не более 10%, и (3) установившаяся ошибка должна быть равна нулю.
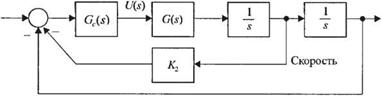
В структурной схеме системы управления рукой робота, изображенной на рис. 7.34, кроме регулятора Gc(s) предусмотрена также обратная связь по скорости. Если рука робота является очень лёгкой и тонкой, то её передаточная функция
С{=)- +4^+Ю004 )(s2 +12^+90036)
(5+10)(52 +25+2501Х. Г +65+22509)
Таким образом, комплексные нули находятся в точках
5 = -2 ± >100 и 5 = - 6 ± >300 , а комплексные полюсы в точках
5 = - 1 ± >50 и 5 = - 3 ± >150.
|
ад Положение руки |
|
|
|
т + Желаемое положение |
|
|
|
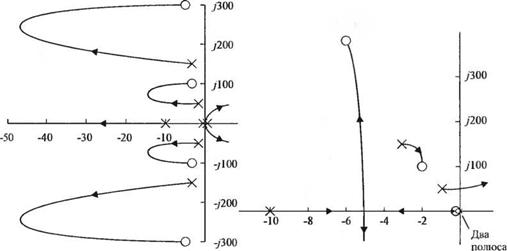
Рис. 7.35. Корневой годограф системы на рис. 7.34 при Gc(s) = Кх, /<2 = 0 и изменении КХ от 0 ДО го |
|
Рис. 7.36. Корневой годограф системы на рис. 7.34 при Gc (s) = Ку после введения нуля в точку s = -0,2 |
|
КХК2 s+ |
|
К |
|
1 |
|
(s |
|
(7.121) |
|
52(5+10)(52 +2s + 2501)(52 +6у+22509) где — коэффициент усиления регулятора Gc(s). Теперь мы можем варьировать два параметра, Кх и К2. Выберем 5 < К2 < 10, чтобы разместить нуль близко к началу координат. При К2 = 5 и изменении параметра Кх корневой годограф имеет вид рис. 7.36. Если Кх = 0,8 иЛ:, = 5, то переходная характеристика системы имеет перерегулирование 12% и время установления 1,8 с. Это — наиболее оптимальный вариант. Если попытаться взять К2 = 1 или К2 = 4, то перерегулирование будет больше допустимого. Следовательно, в системе данной конфигурации мы добились наилучшего качества. Если продолжить процесс синтеза, то можно попытаться, сохранив обратную связь по скорости с коэффициентом К2 = 5, применить регулятор, передаточная функция которого имеет полюс и нуль. Одним из возможных решений является Kx(s+z) |
|
При К2 = 0 и регуляторе, представленном коэффициентом усиления, Gc(s) = Кх, корневой годограф в зависимости от параметра К, изображён на рис. 7.35. Поскольку два корня характеристического уравнения при Кх > 0 всегда находятся в правой полуплоскости, то замкнутая система неустойчива. Ясно, что в данном случае принципиально необходима обратная связь по скорости, К2 > 0. Тогда мы получим H(s) = 1 + K2s, и разомкнутая система будет иметь передаточную функцию 1Л |
|
(s + p) Если теперь выбрать z = 1 и р = 5, то при Кх = 5 мы получим переходную характеристику с перерегулированием 8% и временем установления 1,6 с. |
|
Cr +4s+10004 )(s2 + 12s+ 90036) |
|
Gc(s) = |
|
s2 J |
|
2 У |