СОВРЕМЕННЫЕ СИСТЕМЫ УПРАВЛЕНИЯ
Построение корневого годографа с помощью MATLAB
Приблизительный вид корневого годографа можно получить с помощью последовательности операций, приведённых в табл. 7.2. Альтернативным методом является точное построение корневого годографа с помощью MATLAB. Однако не стоит полагаться только на MATLAB и пренебрегать ручными операциями, определяющими приблизительный вид корневого годографа. Основные принципы корневого годографа воплощены именно в этих ручных операциях, и это особенно важно для полного понимания их смысла.
Этот раздел мы начнём с обсуждения того, как с помощью MATLAB строится корневой годограф. Затем установим связь между разложением на простые дроби, доминирующими полюсами и реакцией замкнутой системы. В заключение рассмотрим применение MATLAB для оценки чувствительности корней.
В данном разделе будут рассмотрены функции rlocus, rlocfind и residue. Функции rlo - cus и rlocfind используются для построения корневого годографа, a residue позволяет получить разложение дробно-рациональных функций на простые дроби.
Построение корневого годографа. Рассмотрим замкнутую систему управления, изображённую на рис. 7.10. Система имеет передаточную функцию
T(S) = *&= *(*+!)(*+3)
R(s) 5(5+2)(s+3)+A:(5+1)'
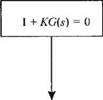
Характеристическое уравнение можно представить в виде:
1 + Я ----------------- =0. (7.122)
ф + 2)(5+3)
Именно в таком виде должно быть записано характеристическое уравнение, чтобы можно было воспользоваться функцией rlocus. Эта функция применяется к характеристическому уравнению общего вида
l+^G(5) = l+^^ = 0, (7.123)
Ф)
где К— варьируемый параметр, изменяемый в диапазоне 0 < К < со. Смысл функции rlocus поясняет рис. 7.37. Этапы построения корневого годографа по уравнению (7.122) приведены на рис. 7.38. Вызов функции rlocus без указания аргументов в левой части автоматически приводит к графическому изображению корневого годографа. При задании аргументов в левой части функция rlocus возвращает матрицу положения корней и вектор соответствующих коэффициентов.
|
|
Рис. 7.37 Функция rlocus
г — положения
комплексных корней К — вектор коэффициентов
t
[r. K]=riocus(sys)
|
6 |
|
|
|
4 |
|
Нуль s = —1 |
|
/ т х о<—е—* А А |
|
о |
|
kJ. |
|
Полюсы s = 0. -2. —3 |
|
Рис. 7.38 Корневой годограф для характеристического уравнения (7.122) |
-6
-6-4 -2 0 2 4 6
Действительная ось
»р=[1 1]; q=[1 5 6 0]; sys=tf(p, q); rlocus(sys)
Корневой годограф: обычный метод
»р=[1 1]; q=[1 5 6 0]; sys=tf(p, q); [r, K]=rlocus(sys); plot(r,’x’)
Корневой годограф: альтернативный метод
Этапы построения корневого годографа с помощью MATLAB таковы:
1. Записать характеристическое уравнение в форме (7.123), где К — варьируемый параметр.
2. Использовать функцию rlocus для построения корневого годографа.
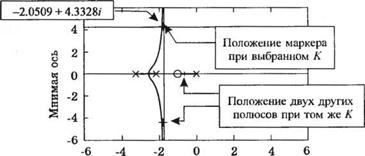
Обратившись к рис. 7.38, мы можем видеть, что при увеличении К две ветви корневого годографа отрываются от действительной оси. Это значит, что при некоторых значениях К характеристическое уравнение замкнутой системы будет иметь два комплексных корня. Предположим, что мы хотим найти значение К, соответствующее этой паре комплексных корней. Для этого можно воспользоваться функцией rlocfind, но только после того, как с помощью функции rlocus будет построен сам корневой годограф. Вызов функции rlocfind приведёт к появлению на корневом годографе маркера в виде черты, пересекающей траекторию. Вы подводите маркер к интересующему вас положению на корневом годографе и нажимаете клавишу Enter. На дисплей будет выведено значение параметра К и координаты выбранной точки. Применение функции rlocfind проиллюстрировано на рис. 7.39.
Продолжая наш пример с построением корневого годографа системы третьего порядка, мы находим, что при К = 20, 5775 передаточная функция замкнутой системы имеет три полюса и два нуля:
|
|
"-2,0505+./4,3227" полюсы: s= -2,0505- /4,3227 ; нули: s =
-0,8989
Если принять во внимание только положение полюсов замкнутой системы, то, казалось бы, доминирующую роль должен играть полюс s = - 0,8989. Чтобы проверить это, имеет смысл исследовать реакцию системы на ступенчатый сигнал, R(s) = 1 Is.
В этом случае мы имеем:
20,5775(5+1)(5+3) 1
5 s(s+2)(s+3)+ 20,5775(5+1) 5
|
|
|
Рис. 7.39 Применение функции rlocfind |
|
Действительная ось |
|
»| |
»р=[1 1]; q=[1 5 6 0]; sys=tf(p, q); rlocus(sys) rlocfind(sys)< і фуНКЦИЯ rlocfind, следующая за функцией rlocus Отметьте точку в графическом окне
|
selected_point = -2.0332 + 4.3416І ans = і------ 20.7453 |
|
Значение К для выбранной точки |
|
Рис. 7.40 Разложение выражения (7.24) на простые дроби |
Первый этап вычисления y(t) состоит в разложении (7.124) на простые дроби. Для этой цели используется функция residue, как показано на рис. 7.40. Смысл этой функции поясняет рис. 7.41.
»К=20.5775; num=K*[1 4 3]; den=[1 5 6+К К 0]; »[r, p,k]=residue(num, den)
г =
|
num den |
|
У(і) = |
|
-1.3786- 1.7010І -1.3786 + 1.7010І -0.2429 3.0000 |
|
r(4) |
|
r( 1) |
|
+ k(s) |
|
Y(s) = |
|
s-p(l) s-p(2) s-p{ 3) s-p( 4) |
|
К2) , к3) |
Р =
|
-2.0505 + 4.3228І -2.0505 - 4.3228І -0.8989 0 |
|
r — вычеты. p — ПОЛЮСЫ, к — постоянный член |
k =
D
|
Рис. 7.41 Функция residue |
|
г — вычеты, р — полюсы, к — постоянный член |
|
Y(s) = |
|
den |
г
[r, p,k]=residue(num, den)
|
км г{1) і г(2) і |
і ф) , |
г ад |
|
*-р(1) s-p{ 2) |
s-p(n) |
Разложение (7.124) на простые дроби выглядит так:
-1,3786+Д7010 -1,3786-Д7010 -0,2429 3
5 ~~ 5 + 2,0505 + >4,3228 + 5 + 2,0505->4,3228 + s+ 0,8989 + 5
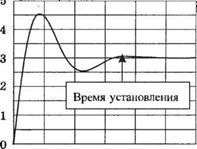
Сравнивая значения вычетов, мы видим, что коэффициент при члене, соответствующем полюсу s = - 0,8989, значительно меньше коэффициентов при членах, соответствующих комплексно-сопряженным полюсам s = - 2,0505 ± >4,3228. Следовательно, можно ожидать, что влияние полюса s = - 0,8989 на реакцию системы _у(/) не будет доминирующим. Тогда время установления следует оценивать по комплексно-сопряженным полюсам. Полюсам s = - 2,0505 ±>4,3228 соответствует коэффициент затухания £ = 0,4286 и собственная частота ю„ = 4,7844. Таким образом, ожидаемое время установления
7>-^—= 1,95с.
Переходная характеристика, построенная с помощью функции step, изображена на рис. 7.42, откуда видно, что Ts ~ 1,6 с. Следовательно, предсказанное значение Тх и 1,95 с является довольно хорошей аппроксимацией. Относительное перерегулирование можно оценить с помощью рис. 5.13, т. к. на вид переходной характеристики будет оказывать влияние и нуль передаточной функции Is), s = - 3. Согласно рис. 5.13, этот показатель равен 60%. В действительности, как показывает рис. 7.42, перерегулирование составляет 50%.
|
|
|
d Ь К Ч С 2 < |
|
0 0.5 1 1.5 2 2.5 3 Время (е) |
Рис. 7.42
Переходная характеристика замкнутой системы на рис. 7.10 при К = 20,5775
»К=20.5775; num=K*[1 4 3]; den=[1 5 6+К К]; sys=tf(num. den); »step(sys)
|
В этом примере мы проиллюстрировали влияние нулей передаточной функции на переходную характеристику системы. Близость нуля л = - 1 к полюсу s = - 0,8989 уменьшает влияние этого полюса, а основной вклад в переходную характеристику вносят комплексно-сопряжённые полюсы s = 2,0505 ± /4,3228 и нуль s = - 3. Сделаем ещё одно замечание в отношении функции residue. Вы можете с её помощью перейти обратно от разложения на сумму простых дробей к дробно-рациональному выражению, задав вычеты (г), положение полюсов (р) и постоянный член (А), как это проиллюстрировано на рис. 7.43. Рис. 7.43 Переход от разложения на простые дроби к дробно-рациональной функции |
|
[num, den]=residuefr, p,k) |
|
Чувствительность и корневой годограф. Корни характеристического уравнения играют важную роль при определении реакции замкнутой системы на входной сигнал. Поэтому крайне полезно иметь оценку чувствительности этих корней к изменению параметров системы. Чувствительность корня г, определяется как дг, |
|
(7.125) |
|
дК/К |
|
Если параметру К придать малое конечное приращение АК и определить новое значение корня г і + Аг,-, то чувствительность будет равна Sr' =-^~ . (7.126) к АК/К Чувствительность S £ — это комплексное число. Вернёмся ещё раз к системе третьего порядка на рис. 7.10 и уравнению 7.122. Если изменить параметр К на 5%, то один из комплексно-сопряжённых полюсов, s = — 2,0505 + /4,3228 получит приращение Аг, = - 0,0025 —/0,1168. Так как параметр К изменился от К = 20,5775 до К - 21,6064, то согласно (7.126) чувствительность будет равна -0,0025-/0,1168 1,0289/ 20,5775 Эту чувствительность можно представить и в иной форме: S'; =2,34е/268Л9 Модуль и аргумент являются показателями чувствительности корня. Программа с помощью которой вычисляется эта чувствительность, приведена на рис. 7.44. Показатель может оказаться очень полезным для сравнения чувствительности по отношению к различным параметрам системы при разных положениях корней. |
|
г — вычеты. р — положение полюсов, к — постоянный член |
|
num den |
|
Y(s) = T(sP(s) = |
|
І |
|
Sk = = _0,0494- /2,3355. |
|
Рис. 7.44 Вычисление чувствительности корня при изменении параметра |
|
Изменение К на 5% |
|
Формула для чувствительности |
|
% Вычисление чуствительности системы % к изменению параметра % К=20.5775; den=[1 5 6+КК]; r1=roots(den); % dK=1.0289; ч - % Km=K+dK; denm=[1 5 6+Km Km]; r2=roots(denm); dr=r1-r2; <----- 1 |
|
% S=dr/(dK/K); |
|
Аг |