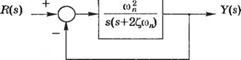СОВРЕМЕННЫЕ СИСТЕМЫ УПРАВЛЕНИЯ

Анализ качества систем управления с помощью MATLAB и Simulink

В этом разделе предметом нашего интереса будут показатели качества, характеризующие реакцию системы на входной сигнал, а также установившаяся ошибка, с которой система отслеживает этот сигнал. Мы завершим дискуссию об упрощении линейных систем. Будет введена в рассмотрение функция MATLAB impulse. Мы еще раз вернемся к функции Isim (введенной в гл. 3) и покажем, как эти две функции используются при имитационном моде - лировании линейных систем. Для той же цели мы воспользуемся и пакетом Simu - f' link. Основы Simulink рассматриваются в Приложении Б, а более подробную ин­формацию о нем с рядом примеров можно найти на Web-сайте MCS.

Качество систем во временной области. Качество системы обычно характеризует­ся ее реакцией на входной сигнал заданного вида. Но поскольку входные сигналы, кото­рые могут реально действовать на систему, заранее неизвестны, то о ее качестве судят по реакции на типовой тестовый входной сигнал. Рассмотрим систему второго порядка, изображенную на рис. 5.35 выходной сигнал в замкнутой системе определяется выраже­нием (в виде изображения по Лапласу):

(5.72)

Рис. 5.35

Одноконтурная система второго порядка

Мы уже знакомы с применением функции step, с помощью которой вычисляется ре­акция системы на ступенчатый входной сигнал. Теперь мы рассмотрим еще один важный тестовый сигнал — импульс. Реакция системы на импульсный сигнал является производ­ной по времени от ее реакции на ступеньку. Мы будем вычислять эту реакцию с помощью функции impulse, схематически изображенной на рис. 5.36.

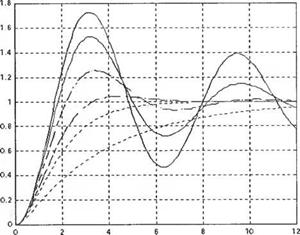
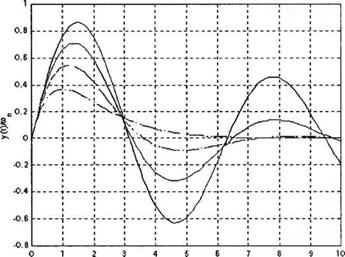
С помощью функции step мы можем построить графики, подобные рис 5.5 (а); они приведены на рис. 5.37. Функция impulse позволит нам получить графики, подобные рис. 5.6. Реакция системы второго порядка на импульсный входной сигнал приведена на рис. 5.38. В скрипте принято со„ = 1, что эквивалентно вычислению реакции системы в функции от со„ I. Этот прием позволяет в общем случае получать графики для любых

П

[у, Т]—impulse (sys, t)

Рис. 5.37

(а) Реакция системы второго порядка

на ступенчатый входной сигнал.

(б) Скрипт MATLAB

Часто возникает необходимость определения реакции системы на произвольный входной сигнал известного вида. В этих случаях используется функция Isim, способ при­менения которой проиллюстрирован на рис. 5.39. С данной функцией мы имели дело в гл. 3, где она применялась к моделям систем в переменных состояния; теперь мы восполь­зуемся функцией Isim в случае, когда система задана своей передаточной функцией. При­мер 5.10 демонстрирует применение функции Isim.

y(t) - реакция в момент t Т — вектор времени моделирования t - моменты времени, в которые вычисляется реакция на входной сигнал

G(s)=sys

Ти

[y, T]=lsim (sys, u, t)

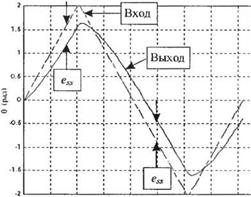
Пример 5.10. Управление рулевым механизмом подвижного робота

На рис. 5.19 изображена структурная схема системы управления рулевым механизмом по­движного робота. Допустим, что регулятор имеет передаточную функцию

G,(s) = Kl + £l.

s

Если входной сигнал является линейным, то установившаяся ошибка

где Kv = К2К. Влияние коэффициента усиления регулятора К2 на установившуюся ошибку оче­видно из (5.73): чем больше К2, тем меньше установившаяся ошибка.

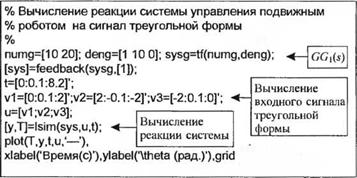
Реакцию замкнутой системы на линейный входной сигнал можно вычислить с помощью функ­ции Isim. В скрипте MATLAB можно предусмотреть ввод различных значений коэффициен­тов Кь К2 и К и тем самым исследоаать их влияние на реакцию системы. На рис. 5.40 приведе­ны результаты, полученные при = I, К2 = 2 и т = 0,1.

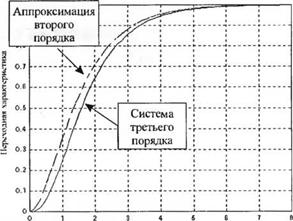
Упрощение линейных систем. Для системы высокого порядка всегда возможно разработать аппроксимирующую модель пониженного порядка, у которой связь между входным и выходным сигналами будет очень близка к аналогичной зависимости для ис­ходной системы. Процедура подобной аппроксимации рассмотрена в разделе 5.10. В сле­дующем примере показано, как с помощью MATLAB можно сравнить реакции исходной системы и аппроксимирующей ее модели.

Пример 5.11. Упрощенная модель

Рассмотрим систему третьего порядка:

Рис. 5.40 а)

(а) Реакция системы управления рулевым механизмом подвижного робота на линейный входной сигнал.

(б) Скрипт MATLAB

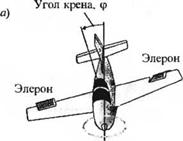
Пример 5.12. Анализ системы управления креном самолета с помощью Simulink

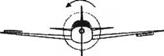
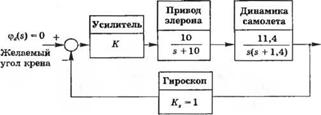
Каждый раз, когда вы летите на самолете, вы на личном опыте можете оценить все достоинст­ва систем автоматического управления, помогающих пилотам вести машину. Точная матема­тическая модель, описывающая поведение самолета в воздухе, представляет собой систему не­линейных дифференциальных уравнений с переменными параметрами. В нашем примере при синтезе автопилота мы воспользуемся упрощенной моделью динамики самолета в виде пере­даточной функции, связывающей отклонение элеронов и угол крена самолета, как это схема­тически показано на рис. 5.42 (а). На рис. 5.42 (б) изображена замкнутая система управления положением самолета в воздухе, цель которой состоит в поддержании угла крена, близкого к нулю градусов, т. е. <р(, = 0, в условиях непредвиденных внешних возмущений.

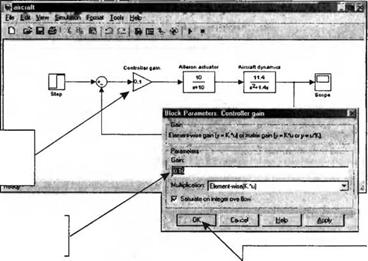
На рис. 5.43 показано, как использовать Simulink для анализа системы управления. Вы можете двойным щелчком кнопки мыши на соответствующем блоке (коэффициент усиления регуля­тора, привод элеронов, динамика самолета, гироскопический датчик крена) открыть всплыва­ющее окно и задать в нем нужные вам параметры. Например, на рис. 5.44 показано, какие дей­ствия надо совершить, чтобы задать коэффициент усиления регулятора. Чтобы всплывающее окно не заслоняло структурную схему, вы можете щелкнуть мышью в любом месте строки за­головка главного окна, а затем щелкнуть на всплывающем окне и перетащить его в нужное по­ложение на рабочем столе.

stepcomp. m

% Сравнительная оуенка переходных характеристик

% His)-

ї3 + bs2 + 1 Is + 6

num1=[6]; den1=[1 6 116]; sys1=tf(num1,den1); num2=[1.6J; den2=[1 2.584 16]; sys2=tf(num2,den2); t=[0:0.1:8];

[y1,T1]=step(sys1,t);

[y2,T2]=step(sys2,t); plot(T 1 ,у1 ,Т2,у2,‘—'),grid хІаЬеІ(‘Время (с)‘),уІаЬеІ(‘Переходная характеристика1)

Плоскость

симметрии

б)

Сел troll «і «яш Aileron actuate»

Ш—9—Е>

О

Как только вы измените параметры во всплывающих окнах, они сразу же появятся и на струк­турной схеме. На рис. 5.45 и 5.46 показаны открытые окна для задания динамики привода эле­ронов и самолета. Основными элементами системы управления являются регулятор, Gc(s) = К, привод элеронов.

г / 10

G„(s) = -

j+10

и самолет,

11.4

2 1 s + 1,4s

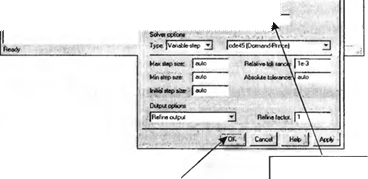
Перед началом решения задачи необходимо установить время окончания моделирования. Для этого в меню Simulation выберите опцию Parameters, как показано на рис. 5.47. Всплывающее окно Simulation Parameters дает доступ к различным программам численного интегрирова­ния и позволяет задать время начала и окончания моделирования.

Произведя необходимые изменения, нажмите кнопку ОК. Для начала моделирования выбери­те опцию Start из меню Simulation, как показано на рис. 5.48. в результате программа присту-

block Pdiameter-. Aileton dcluatur

j* " •*—

- : Wjttwwpcwtmic* denombsWf.

лСМріДЙ^вдоіЬІЬегшІ^.^іоміпімгммикх. Coef&atritBr ;Кх<Ы59п*врсж(*»<**, '-n;V<

-P«fne*e»:

*h№Mtct

Щщ —

Denonfoala.,

ІйвдГ

•і ''***'<*■'“ ___

]м*о

—г^"“......

^|£ЖРІ с««* Ґ а* І ьф І

Введите сюда коэффициенты полиномов в числителе и знаменателе

Рис. 5.46

Всплывающее окно, используемое для изменения передаточной функции самолета

J

Введите сюда коэффициенты полиномов в числителе и знаменателе

пит к решению задачи и будет делать это пока не наступит заданный момент окончания моде­лирования. Вы также можете начать и прервать моделирование с помощью кнопки панели ин­струментов, как показано на рис. 5.48.

Вывод на экран графика решения задачи производится при помощи опции Scope (см. Прило­жение Б). На рис. 5.49 приведен результат моделирования для случая, когда задан коэффици­ент усиления регулятора К = 0,16. Вы можете изменить любую передаточную функцию или любой параметр и оперативно наблюдать, как это отразится на решении задачи.

Ш—*9—

Для начала моделирования щелкните на Start

/

Моделирование можно также начать нажатием этой кнопки

Controller (jam Ailtion actuator Aircraft dynamic*

Ш **>->£>

-o-

Start the fimulatiofi