СОВРЕМЕННЫЕ СИСТЕМЫ УПРАВЛЕНИЯ
Пример синтеза: управление ориентацией телескопа «Хаббл»
Орбитальный космический телескоп «Хаббл» является самым сложным и дорогим прибором научных исследований из всех, которые когда-либо были созданы. Этот телескоп, запущенный 24 апреля 1990 г. на орбиту высотой 610 км над поверхностью Земли, существенно раздвинул границы технических возможностей. Его зеркало диаметром 2,4 м имеет самую гладкую поверхность среди всех когда-либо созданных зеркал, а его система наведения способна обеспечить ориентацию на центр 10-центовой монеты, находящейся на
расстоянии 650 км. Зеркало имеет сферическую аберрацию, которая во время экспедиций на шаттле в 1993 и 1997 гг. была подвергнута существенной коррекции. Рассмотрим модель системы управления ориентацией телескопа, изображенную на рис. 5.34.
Цель синтеза состоит в выборе таких значений Кх и К, чтобы (1) относительное перерегулирование выходной переменной при ступенчатом задающем сигнале /■(/) не превышало 10%, (2) установившаяся ошибка при линейном входном сигнале была минимальной и (3) был значительно снижен эффект от ступенчатого возмущения. Поскольку система содержит внутренний контур, то прежде всего необходимо упростить структурную схему, сведя ее к виду рис. 5.34 (б).
Для системы на рис. 5.34 (б) выражение для выхода, обусловленного двумя входными сигналами, можно получить с помощью формулы Мейсона:
Y(s) = T(s)R(s) + [7ф/ОД5) , (5.67)
где
KG(s) _KG(s) i+a:g(s) і+Д5)‘
Для ошибки имеем:
E(s) = —-—R(s)—^-D(s). (5.68)
l + i(j) 1+Z.(s)
Сначала выберем такие значения К и Кх, которые удовлетворяли бы ограничению на относительное перерегулирование при ступенчатом входном сигнале, R(s) = A/s. Полагая D(s) - 0, запишем:
Y(s)= -~^^R(s)= * А=—^-------- А . (5.69)
l+A:G(j) sis+K^+K s s-+K{s+K S
Чтобы обеспечить перерегулирование менее 10%, используя рис. 5.8, выберем С, = 0,6; также на основании (5.16) определим, что при С, = 0,6 перерегулирование составит 9,5%. Далее исследуем установившуюся ошибку при линейном входном сигнале r(t)=Bt, t > 0. На основании (5.28) имеем:
|
В (5.70) |
В
|
К/Кх |
в» =lim
л-»0
sKG(s)
Установившаяся ошибка при единичном ступенчатом возмушении равна —l/К. (Убедитесь в этом самостоятельно.) Зависимость ошибки от возмущения можно уменьшить путем увеличения К [см. (5.68)]. Подводя итоги, нам необходимо иметь большое значение К и большое отношение К/Кх, чтобы получить малое значение установившейся ошибки при линейном входном сигнале [см. (5.70)]. Однако сохраняется требование иметь С, = 0,6, чтобы ограничить величину перерегулирования.
В нашей задаче прежде всего надо выбрать величину К. При С, = 0,6 характеристическое уравнение системы имеет вид:
s2 + 2£av + со* = s2 + 2 ■ (0,6) со,^ + К = 0. (5.71)
Следовательно, со„ = 4к, и второй член в знаменателе (5.69) должен давать/^ = 2 (0,6) ш„. Тогда, = 1,24к, или отношение К/Кл принимает вид
К _ к _4к Кх 1,24К 1,2 '
|
|
|
Возмущение D(s) |
|
Усилитель |
|
а) R(s) Задание |
|
Динамика телескопа |
|
. Л*) Положение |
|
К |
|
б) |
|
+^£(в) |
|
R (s) |
|
К |
|
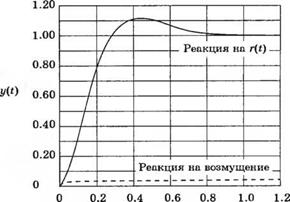
Рис. 5.34 (а) Система управления ориентацией телескопа «Хаббл», (б) преобразованная структурная схема, (я) синтезированная система и (г) реакции системы на единичные ступенчатые задающий и возмущающий сигналы |
|
+ |
G(s) |
||
|
1 |
|||
|
) *■ |
s(s+Kj) |
|
Y(s) |
|
Kxs |
|
£(s) |
100 |
-Jury— |
1 |
|
|
? ' |
s(s+12) |
|||
|
D{s) |
|
Y(s) |
|
в) B(s) |
|
t (с) |
Если выбрать К= 25, то мы получим Кх = 6 и ЮКХ = 4,17. Если же выбрать К= 100, то мы получим = 12 и KJKX = 8,3 3. В действительности мы не можем безгранично увеличивать К,
чтобы система не выходила из линейного режима работы. При значении /С = 100 структурная схема системы имеет вид рис. 5.34 (в). Реакция системы на единичные ступенчатые воздействия со стороны задания и возмущения изображены ни рис. 5.34 (г). Обратите внимание, что влияние возмущения является крайне незначительным.
В завершение заметим, что установившаяся ошибка при линейном входном сигнале [см.(5.70)] равна
|
|
Таким образом, при АГ = 100 решение задачи синтеза системы можно считать превосходным.