СОВРЕМЕННЫЕ СИСТЕМЫ УПРАВЛЕНИЯ
Пример синтеза с продолжением: система чтения информации с диска
|
□ |
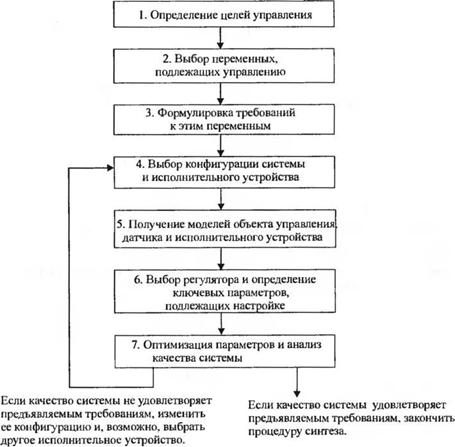
В разделе 4.10 мы рассматривали поведение замкнутой системы управления положением считывающей головки. Обратимся еще раз к этой системе, структурная схема которой приведена на рис. 4.33. Здесь мы продолжим процедуру синтеза (последовательность действий вторично представлена на рис. 5.50) и перейдем к шагу 3, на котором определяется желаемое качество системы. Мы попытаемся выбрать такое значение коэффициента усиления Ка, при котором качество системы было бы наилучшим.
Рис. 5.49
|
|
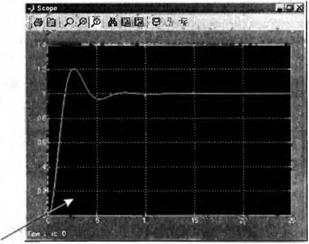
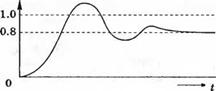
Реакция на ступенчатый входной сигнал системы управления углом крена самолета, полученная путем моделирования в Simulink
Щелкните правой кнопкой мыши в области экрана, чтобы вызвать всплывающее окно для задания параметров графика
|
|
Нашей целью является получение наилучшего быстродействия при отработке ступенчатого сигнала r(t) с учетом (1) ограничения на величину перерегулирования и колебательный характер реакции и (2) необходимости уменьшения влияния возмущения на положение считывающей головки. Требования к качеству системы сведены в табл. 5.8
|
Таблица 5.8. Требования к переходной характеристике
|
Рассмотрим модель второго порядка для двигателя и рычага, в которой мы пренебрегли индуктивностью обмотки двигателя. В этом случае замкнутая система имеет вид рис. 5.51. Для входной переменной при условии D(s) = 0 можно записать:
У(Д)= — R(s) = , 5К°-------- R(s) = ------- ^--------- T R(sy (5.74)
5(5+20)+5/С 0 s' +20s+5Ka s~ +2Cfi>„s+w~
|
D(s)
Рис. 5.51. Модель системы управления второго порядка |
|
R(s) |
r(s)
Отсюда следует, что cof, = 5Ка и 2£со„ = 20. Далее мы можем определить реакцию системы с помощью скрипта MATLAB, приведенного на рис. 5.52. В табл. 5.9 представлены показатели качества, соответствующие различным значениям Ка.
|
Таблица 5.9. Реакция системы второго порядка на ступенчатый входной сигнал
|
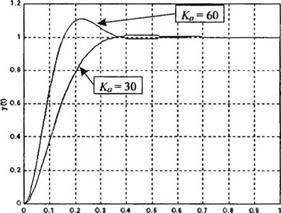
Рис. 5.52 а)
Реакция системы на единичный ступенчатый входной сигнал, rt) = 1. / > 0.
(а) Скрипт MATLAB.
(б) Реакции системы при Ка = 30 и Ка — 60
Ка=30; ч-----------------------------------
t=[0:0.01:1];
nc=[Ka*5]; dc=[1]; sysc=tf(nc, dc); ng=[1]; dg=[1 20 0]; sysg=tf(ng. dg) sys1=series(sysc, sysg); sys=feedback(sys1 ,[1]); J" [y. T]=step(sys, t); plot(T. y),grid хІаЬеІ(‘Время (c)‘) ylabel(‘y(t)’)
Выбор K„
Вычисление передаточной функции замкнутой системы
|
Нреэде іеі |
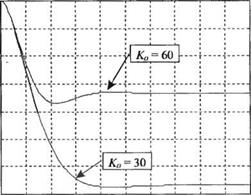
Нарис. 5.53 изображены зависимости^/), полученные при единичном ступенчатом возмущении для Ка = 30 и Ка = 60. При увеличении Ки до 60 влияние возмущения уменьшается почти в 2 раза. Если мы хотим удовлетворить требования, предъявляемые к системе, то нам придется выбрать компромиссное значение Ка. Очевидно, в данном случае наилучшим компромиссом будет значение Ка = 40. Однако это значение не удовлетворяет всем требованиям. В следующей главе мы вернемся к процедуре синтеза, изображенной на рис. 5.50, и изменим конфигурацию системы, как это предусмотрено шагом 4.
Резюме
В этой глав мы познакомились с определением качества системы управления и способами его измерения. Было обсуждено понятие показателей качества и подчеркнута важность использования типовых тестовых сигналов. Были приведены некоторые показатели качества, характеризующие систему при типовых тестовых сигналах. Сюда относятся, например, перереіулирование, время максимума и время установления переходной характеристики при ступенчатом входном сигнале. Было отмечено, что часто требования к качеству системы вступают в противоречие и требуется компромиссное решение. Была рассмотрена связь между расположением на j-плоскости корней характеристического уравнения системы и ее временными характеристиками. Наиболее важным показателем качества системы является ее установившаяся ошибка при входном сигнале заданного вида. Эта зависимость
Рис. 5.53 а)
Реакция системы на единичное ступенчатое возмущение,
D{s) = 1/s.
(а) Скрипт MATLAB.
(б) Реакции системы при Ка — 30 и Ка = 60
|
t—[0:0.01:1]; пс=[Ка*5]; dc=[1]; sysc=tf(nc, dc); ng=[1]; dg=[1 20 0]; sysg=tf(ng, dg); sys=feedback(sy sg ,sysc); |
Выбор Kc, |
|
|
Возмущение приложено к сумматору со знаком минус |
||
|
sys—sys; ^ step(sys. t); |
||
|
хІаЬеІ(‘Время (c)‘) ylabel('y(t)’) |
б)
|
0 0.1 0 2 0.3 0.4 0.6 0.6 0.7 0.8 0.9 1 Время(с> |
|
|
|
о х Я И |
|
10 Время (с) |
была установлена с помошью теоремы о конечном значении функции. Данное свойство системы с обратной связью проиллюстрировано на рис. 5.54. В заключение была подчеркнута важность применения интегральных оценок качества, и на ряде примеров было показано, как можно минимизировать соответствующую оценку. Таким образом мы сделали акцент на определение и количественные оценки качества систем управления с обратной связью.
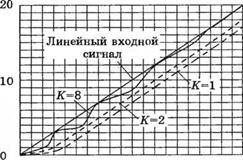
Рис. 5.54
Реакция системы с обратной связью на линейный входной сигнал при К = 1. 2 и 8 в случае С (s) = K/s[s + 1)(s + 3). Установившаяся ошибка уменьшается с ростом К но приобретает колебательный характер при К = 8
|
Упражнения У-5.1. Система управления двигателем дисковода компьютера должна ослаблять влияние возмуще- У-5.2. На рис. 5.2(У) изображена модель Ответ: (а) еЛЛ = /4/11; (б) 20,8%. У-5.3. Долгие годы железнодорожная компания Амтрак пытается привлечь пассажиров для поездок Использование магнитной подушки и электромагнитной силовой установки обеспечивает Рис. 5.3 (У) Система управления |
|
Динамика |
|||
|
изменения |
|||
|
зазора |
|||
|
л |
К |
- Y( s) |
|
|
J |
s(s+14) |
Зазор |
|
т _ Ток в обмотке электромагнита |
|
Автомобиль |
|
100 |
|
ад Заданная скорость |
|
о- |
|
Скорость |
|
(s+2)(s+5) |
|
Рис. 5.2 (У). Система управления скоростью гоночного автомобиля |
|
|
|
б) |
На рис. 5.3(У), (б) изображена система управления подвеской вагона, (а) С помощью табл. 5.6 выберите значение К. обеспечивающее оптимальную реакцию системы на ступенчатый входной сигнал по критерию ИВМО. (б) С помощью рис. 5.8 определите ожидаемое перерегулирование при ступенчатом входном сигнале I(s).
Ответ: К = 100; 4,6%.
У-5.4. Система в разомкнутом состоянии имеет передаточную функцию
.s(j+ 4)
(а) Определите передаточную функцию замкнутой системы с единичной отрицательной обратной связью, T(s) = Y(s)/R(s). (б) Определите реакцию системы у(1) на ступенчатый входной сигнал r(0 = A, t > 0. (в) С помощью рис. 5.13(a) определите относительное перерегулирование. (г) Используя теорему о конечном значении, определите установившееся значение^*). Ответ, (б) у(() = 1— 1,07е'3' sin(V7» + 1,2) .
У-5.5. На рис. 5.5(У), (а) изображен малоинерционный плоттер, а на рис 5.5(У),(б) — его структурная схема, (а) Определите установившуюся ошибку при линейном входном сигнале, (б) Выберите значение К. обеспечивающее максимально возможное быстродействие системы при отсутствии перерегулирования.
Укажите положение полюсов и нулей данной системы и обсудите доминирующую роль комплексных полюсов. Какое перерегулирование вы ожидаете в случае ступенчатого входного сигнала?
|
|
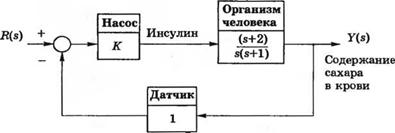
У-5.6. Существенную помощь людям, страдающим диабетом, может оказать система автоматической инъекции инсулина, включающая в себя насос и датчик, измеряющий содержание сахара в крови. Структурная схема такой системы изображена на рис. 5.6(У). Выберите значение К, при котором реакция системы на ступенчатое входное воздействие имела бы перерегулирова-
Рис. 5.5 (У) а)
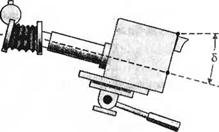
(а) Плоттер фирмы Хьюлетт-Паккард.
|
Y(s) Положение |
(б) Структурная схема плоттера
|
|
|
Рис. 5.6 (У) Система управления содержанием сахара е крови |
|
ние порядка 7%. На схеме R(s) соответствует желаемому содержанию сахара в крови, a Y(s) — его действительному значению. (Подсказка: воспользуйтесь рис.5.13(a).) Ответ: К = 1,67. У-5.7. Система позиционирования головки дисковода гибкого диска в замкнутом состоянии имеет передаточную функцию 0,313(5+ 0,8) (s + 0,6)(s2 + 4s + 5) Изобразите диаграмму расположения полюсов и нулей данной системы и обсудите доминирующую роль комплексных полюсов. Какое перерегулирование можно ожидать при ступенчатом входном сигнале? У-5.8. Система, передаточная функция которой в разомкнутом состоянии имеет вид G(s) =---------------------- , s(s+yl2K) охвачена единичной отрицательной обратной связью. (а) Определите относительное перерегулирование и время установления (по критерию 2% от конечного значения) при отработке единичного ступенчатого входного сигнала. (б) При каких значениях К время установления будет менее 1 с? У-5.9. Система управления второго порядка имеет в замкнутом состоянии передаточную функцию T(s) = Y(s)/R(s). При ступенчатом входном воздействии к качеству системы предъявляются следующие требования: 1) Относительное перерегулирование < 5%; 2) Время установления < 4 с ; 3) Время максимума переходной характеристики Тр < 1 с. Укажите допустимую область расположения полюсов T(s), при которой будут обеспечены выдвинутые требования. Время установления определяется по критерию 2% от конечного значения. У-5.10. На рис. 5.10(У) изображена система с единичной отрицательной обратной связью. Определите установившуюся ошибку при ступенчатом и линейном входных сигналах, если 10(s+4) |
|
s(s+l)(s+3)(s+8) У-5.11. Всем известна карусель Ферриса, используемая в качестве аттракциона на ярмарках и карнавалах. Джордж Феррис родился в 1859 г. в Гейлс- берге, шт. Иллинойс. Позже он переехал в Неваду и в 1881 г. закончил Ренсселерский политехнический институт. К 1891 г. Феррис уже имел большой опыт строительства металлических конструкций и мостов. Он задумал и построил свою знаменитую карусель для выставки в честь Колумба, проходившей в Чикаго в 1893 г. Во избежание падения пассажиров потребуем, чтобы |
|
G(s) = - |
|
*<s>_Lq |
|
Y(s) |
|
G(s) |
|
Рис. 5.10 (У). Система с единичной обратной связью |
|
Возмущение D(s) |
|
Динамика карусели и привода |
|
(s+2)(s+4) |
|
|
|
F(s) |
|
Ка) |
|
(s+6) |
|
Скорость вращения |
|
Желаемая скорость |
|
Регулятор |
|
|
к |
|
|
(s+9) |
Рис. 5.11 (У). Регулирование скорости вращения карусели Ферриса
в системе на рис. 5.11(У) установившаяся скорость удерживалась в пределах 5% от желаемой скорости.
(а) Определите значение К, при котором будет выполняться предъявляемое к системе требование. (б) При коэффициенте К, найденном в п. (а), вычислите и изобразите графически ошибку e(t), вызванную возмущением D(s) = 1/ s. Изменяется ли при этом скорость более чем на 5%? [Для простоты вычислений примите R(s) = 0.]
У-5.12. Для системы с единичной обратной связью на рис. 5.10(У) определите установившуюся ошибку в случае ступенчатого и линейного входных сигналов, если
10
G(s) = — .
s + 14s + 50
оо при линейном входном сигнале.
Ответ: ess = 0,83 при ступенчатом сигнале и е(,
|
Рис. 5.13 (У). Система с обратной связью |
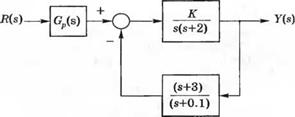
У-5.13. Нарис. 5.13(У) изображена система с обратной связью.
(а) Определите установившуюся ошибку при единичном ступенчатом входном сигнале, если К = 0,4 и Gp(s) = 1.
(б) Выберите такое значение Gp(s). при котором в случае единичного ступенчатого входного сигнала установившаяся ошибка будет равна нулю.
У-5.14. Замкнутая система управления имеет передаточную функцию
Г(,) = М = яо.
R(s) (s + 10)(s2 + 10s+50)
В случае ступенчатого входного сигнала R(s) постройте графикиy(t), если (а) используется исходное выражение T(s) и (б) используются только доминирующие комплексные полюсы. Сравните результаты.
У-5.15. Дана система второго порядка:
г, , У(s) (10/z)(s + z)
R(s) (s + l)(s + 8)
Рассмотрите случай, когда 1 < z < 8. Разложите T(s) на простые дроби и изобразите графики >(7) в случае ступенчатого входного сигнала r(t) для значений z = 2; 4; 6.
У-5.16. Передаточная функция замкнутой системы T(s) имеет два доминирующих комплексно-сопряженных полюса. Выделите в левой половине s-плоскости область, в которой должны находиться эти полюсы, чтобы система удовлетворяла следующим требованиям.
(а) 0,6 < С, < 0.8 и ы„ < 10.
(б) 0,5 < <; < 0,707 и со,, > 10.
(в) С > 0,5 и 5 < со„ < 10. «)
|
y(t) |
(г) С < 0,707 и 5 < ы„ < 10.
(д) С > 0,6 со„ < 6.
|
Рис. 5.17 (У) |
У-5.17. Для системы, изображенной на рис.5.17(У), (а), реакция на единичное ступенчатое воздействие б)
при К = 1 приведена на рис. 5.17(У), (б). Определите значение К, при котором установившаяся ошибка равнялась бы нулю.
Ответ: К = 1,25.
Задачи
3-5.1. В телевидении серьезную проблему представляют скачки или подергивания изображения, возникающие из-за перемещения камеры. Этот эффект особенно проявляется тогда, когда камера находится на движущемся автомобиле или на самолете. Чтобы исключить это явление, специально была спроектирована система Диналенс, изображенная на рис. 5.1(3). Предполагается, что максимальная скорость сканирования составит 25 °/с. Будем считать, что Kg = К, = 1, а постоянной времени можно пренебречь, (а) Получите выражение для ошибки системы Е(s). (б) Определите, каким должен быть коэффициент усиления в контуре, КдКщКр если допускается установившаяся ошибка в 1 °/с. (в) Двигатель имеет постоянную времени тш = 0,40 с. Определите, каким должен бьггь коэффициент усиления в контуре, чтобы время установления (по критерию 2% от конечного значения vt) не превышало 0,03 с.
3-5.2. Необходимо синтезировать замкнутую систему управления, которая обладала бы передемп - фированной реакцией на ступенчатое входное воздействие. К качеству системы предъявляются следующие требования:
20% > относительное перерегулирование > 10%; время установления < 0,6 с.
|
а) Момент двигателя |
Рис. 5.1 (3)
|
Камера |
|
|
Система управления телекамерой
|
б) Vc |
Гироскоп |
Усилитель |
Двигатель |
||
|
кв |
+ |
Ка |
кт |
||
|
Скорость |
STg+1 |
STm+l |
|
камеры Тахогенератор |
|
Скорость мехов |
К,
(а) Укажите желаемую область расположения доминирующих полюсов системы, (б) Определите наименьшее значение третьего полюса, если реакция в основном должна определяться комплексно-сопряженными полюсами, (в) Передаточная функция замкнутой системы T(s) (при единичной обратной связи) имеет третий порядок. Определите передаточную функцию прямой цепи G(s) = Y(s)/E(s), если задано время установления (по критерию 2% от конечного значения) 0,6 с и относительное перерегулирование 20%.
|
|
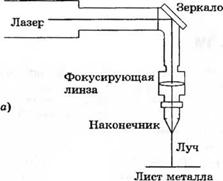
3-5.3. Лазерный луч можно использовать для сварки, сверления, гравировки, резки и разметки металлических деталей, как показано на рис. 5.3(3), (а). Предположим, что нам необходимо с помощью замкнутой системы управления на рис. 5.3(3), (б) начертить на металле параболическую линию. Определите, каким должен быть коэффициент усиления, чтобы при r(t) = Г см установившаяся ошибка составляла не более 5 мм.
Рис. 5.3 (3)
Система управления лучом лазера
|
б) |
|
r(s) |
|
R(s> |
|
к |
|||
|
г |
S2 |
||
3-5.4. Разомкнутая система имеет передаточную функцию
п, л К G(s) =-- .
s(s + 2)
При замыкании единичной отрицательной обратной связи реакция системы на ступенчатый входной сигнал должна удовлетворять следующим требованиям:
время максимума Тр= 1,1 с; относительное перерегулирование = 5%.
(а) Определите, могут ли оба требования быть удовлетворены одновременно, (б) Если невозможно одновременно удовлетворить оба требования, то определите компромиссное значение К. при котором показатели качества меньше всего отличались бы от заданных.
3-5.5. Для выполнения астрономических наблюдений на орбиту выводится космический телескоп. Система управления наведением должна обладать точностью 0,01 угловой минуты и следить за движением объектов со скоростями до 0,21 угловой минуты в секунду. Космический телескоп изображен на рис. 5.5(3), (а), а система управления — на рис.5.5(3), (б). Пусть т, = 1 с, а т2 = 0 (примем такую аппроксимацию), (а) Определите значение К = К, К2, при котором реакция на ступенчатый входной сигнал будет иметь как можно меньшее время установления, а перерегулирование не будет превышать 5%. (б) Определите установившуюся ошибку системы при отработке ступенчатого и линейного входных сигналов, (в) Определите значение К, К2 для системы, оптимальной по критерию ИВМО, в случае (1) ступенчатого и (2) линейного входного сигнала.
|
а) |
 Наземная станция
Наземная станция
|
Рис. 5.5 (3). (а) Космический телескоп, (б) Система управления наведением телескопа |
|
|
|
б) |
|
F(s) Угловое положение |
|
ж ко |
|
а) |
|
10 20 30 40 Время (с) |
|
б) |
|
Y(s) Траектория движения |
|
R(s) |
|
О |
|
G(s) |
|
3-5.6. Робот запрограммирован так, чтобы обеспечивать движение инструмента по заданной траектории. Пусть эта траектория представлена графиком пилообразного вида на рис. 5.6(3), (а). В системе нарис. 5.6(3), (б) передаточная функция G(s) имеет вид: 50(s +1) |
|
s(s + 6 )(s + 9) |
|
G(s) = |
Определите установившуюся ошибку.
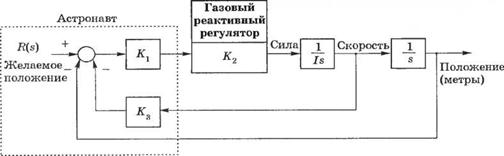
3-5.7. Астронавт Брюс МакКендлесс 7 февраля 1984 года совершил первую прогулку в космосе без страховочного фала, используя газовый реактивный двигатель. Его фото во время этой прогулки приведено на рис. 5.7(3), (а). Регулятор можно представить в виде коэффициента К2, как показано на рис. 5.7(3), (б). Момент инерции человека вместе с оборудованием, которое он держит в руках, составляет 25 кг • м2. (а) Определите значение коэффициента К3, необходимое для поддержания установившейся ошибки, равной 1 см, при входном воздействии r(t) = / (в метрах), (б) Приняв это значение К3, определите коэффициент КХК2, при котором величина перерегулирования не будет превышать 10%. (в) Аналитически найдите величину КХК2, при которой в случае ступенчатого входного сигнала оценка качества ИКО будет минимальной.
Рис. 5.6 (3). Управление движением робота
Рис 5.7 (3)
|
|
(а) Астронавт Брюс МакКендпесс в нескольких метрах от находящегося на орбите космического челнока «Челленджер».
Он пользуется управляемым вручную реактивным устройством, создающим струю газа азота.
(б) Структурная схема системы
|
а)
|
6)
3-5.8. Солнечные батареи генерируют напряжение постоянного тока, которое может быть использовано для питания электродвигателей или преобразовано в напряжение переменного тока, направляемое в электросеть. Мощность на выходе батарей желательно поддерживать максимальной, независимо от изменения положения Солнца в течение дня. Одна из возможных систем, предназначенных для решения этой задачи, приведена на рис. 5.8(3). Передаточная функция объекта
G(s) = -^—. s+10
где К = 20. Определите (а) постоянную времени замкнутой системы и (б) время установления (по критерию 2% от конечного значения выходной переменной) при действии возмущения (например, при появлении облаков).
Возмущение
|
P(t) Выходная мощность |
Производная мощности ■+
при ее ------------ *
максимальном
уровне
|
Интегратор |
-1 |
|
|
-А— |
G(s) |
|
|
S |
+ w |
|
о- |
|
Дифференциатор H(s) |
|
dp dt |
3-5.9. Антенна, с помощью которой осуществляется связь с телекоммуникационным спутником Телстар, является самой крупной из когда-либо построенных антенн рожкообразной формы. Эта антенна. работающая в сантиметровом диапазоне, имеет длину 54 м, весит 340 т и вращается на рельсах по окружности.
|
|
На рис. 5.9(3) приведено фото этой антенны. Спутник Телстар имеет диаметр 85 см и вращается вокруг Земли на высоте 4000 км со скоростью 26000 км/ч.
Антенна должна быть направлена на спутник с точностью 0,1°. т. к. микроволновый луч имеет ширину 0,2° и сильно уменьшает свою мощность с уве - Рис. 5.9 (3). Антенна для связи
личением расстояния. Если антенна со спутником Телстар в Андовере, шт. Мэн должна следить за движущимся спутником, определите, какое значение Kv для этого должна иметь система управления.
3-5.10. При управлении по цепи якоря скоростью вращения двигателя постоянного тока в качестве сигнала обратной связи используется япротивоЭДС. (а) Изобразите структурную схему такой системы (см. пример 2.5). (б) Определите установившуюся ошибку системы, если на вход подается ступенчатый сигнал, в соответствии с которым скорость должна принять новое значение. Примите Ra = La = J-b = Km = Kh= 1. (в) Выберите коэффициент противоЭДС таким образом, чтобы переходная характеристика имела перерегулирование 15%.
3-5.11. Разомкнутая система имеет передаточную функцию
cw=fr--
E(s) s
Данная система охватывается единичной отрицательной обратной связью, и на вход подается ступенчатый сигнал амплитуды А. Задано начальное условие y(t0) = О, где y(t) — выходной сигнал системы. Качество системы определяется оценкой
1 = fe2(t)dl.
Jo
(а) Покажите, что 1 = (A - Q)2I2K. (б) Определите параметр К, минимизирующий данную оценку качества. Имеет ли этот коэффициент практическую ценность? (в) Выберите величину К, имеющую практический смысл, и определите соответствующее значение оценки качества.
3-5.12. По мере создания высокоскоростных электропоездов будет возрастат ь интенсивност ь пассажиропотоков, т. к. поездка из города в город по времени станет сравнима с авиаперелетом. В Японии между Токио и Осакой уже циркулирует экспресс, покрывающий расстояние в 515 км за 3 ч 10 мин со средней скоростью 163 км/ч. Эта скорость еще более увеличится при использовании новых систем, таких как магнитная подвеска над алюминиевым направляющим рельсом. Для поддержания заданной скорости предлагается система управления, обеспечивающая нулевую установившуюся ошибку при линейном входном сигнале. Для этого достаточно иметь систему третьего порядка. Определите оптимальную передаточную функцию замкнутой системы T(s), исходя из оценки качества ИВМО. Оцените время установления (по критерию 2% от конечного значения) и перерегулирование при ступенчатом входном сигнале, если (о„ = 10.
3-5.13. Систему четвертого порядка требуется аппроксимировать моделью более низкого порядка. Исходная система имеет передаточную функцию
, s3+7s2 + 24s+24 s3 + 7s2 + 24s+24
H(S) = 5-------- ^------------------ =---------------------------------------- .
s4 + 10s3 + 35s2 + 50s +24 (s + l)(s + 2)(s + 3)(s + 4)
Покажите, что применение метода, описанного в разделе 5.10, если не заданы полюсы и нуль L(s), позволит получить модель второго порядка с передаточной функцией _ 0,2917s + 1 0,731(5 + 3,428)
5 0,399s2 + 1,375s +1 (s+ l,043)(s+ 2,4)
3-5.14. Для исходной системы из задачи 5.13 требуется получить модель пониженного (второго) порядка, если заданы ее полюсы, равные -1 и -2, а ее единственный нуль не определен. Покажите, что эта модель имеет передаточную функцию
r. . 0,986s + 2 0,986(s + 2,028)
±jS ) » — .
s + 3s + 2 (s+ l)(s+ 2)
|
|
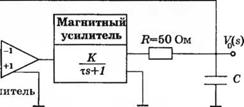
3-5.15. На рис. 5.15(3) изображен
магнитный усилитель с малым
выходным сопротивлением,
соединенный последовательно
с низкочастотным фильтром и тг, ч
Тг K(s) *
предусилителем. Усилитель *
имеет высокое входное сопротивление, коэффициент усиле-
ния. равный 1. и используется рис. 515 (3). усилитель с обратной связью
в качестве сумматора. Выберите значение емкости С так, чтобы передаточная функция K0(s)/K,(s) имела коэффициент затухания 1/V2. Постоянная времени
магнитного усилителя т = 1 с, а его коэффициент усиления К = 10. Определите время установления (по критерию 2%) для данной системы.
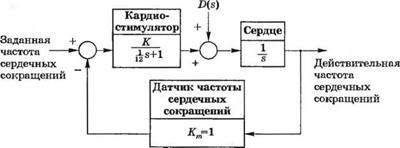
3-5.16. Электрокардиостиму лятор способен регулировать частоту сердечных сокращений. На рис. 5.16(3) изображена замкнутая система, включающая в себя кардиостимулятор и датчик частоты сердечных сокращений. Передаточная функция кардиостимулятора и объекта управления (сердца) имеет вид:
G(s) = — .
s(s/12+ 1)
Определите коэффициент К. при котором в случае ступенчатого возмущения время установления будет менее 1 с. Перерегулирование реакции на ступенчатое изменение заданной частоты сердечных сокращений не должно превышать 10%. (а) Определите подходящий диапазон значений К. (б) Если номинальное значение К = 10, определите чувствительность системы к малым изменениям К. (в) Оцените чувствительность из п. (б) на нулевой частоте (при s = 0).
(г) Оцените величину чувствительности при нормальной частоте сердечных сокращений 60 ударов/ мин.
|
Возмущение
|
3-5.17. Обратитесь к исходной системе третьего порядка из примера 5.9. Определите аппроксимирующую модель первого порядка, в которой нуль отсутствует, а полюс не задан.
3-5.18. В замкнутой системе управления с единичной отрицательной обратной связью прямая цепь имеет передаточную функцию
G(s) = ^—1----------
s(s + 6s+ 12)
(а) Определите передаточную функцию замкнутой системы T(s). (б) С помощью метода, описанного в разделе 5.10, аппроксимируйте T(s) моделью второго порядка, (в) С помощью MATLAB или любой другой компьютерной программы постройте графики реакции исходной системы и ее аппроксимации на единичный ступенчатый сигнал и сравните полученные результаты.
|
К |
|||
|
(s+10)(s+12) |
|||
|
Y(s) |
|
Кг |
3-5.19. Рассмотрите систему, изображенную на рис. 5.19(3). (а) Пола - гая £(s) = R(s) - T(s), определите зависимость установившейся ошибки т К и Ку в случае единичного ступенчатого входного Рис 519 (3). Система с предусилителем К, сигнала, (б) Выберите значение
Ку так, чтобы установившаяся ошибка была равна нулю.
Задачи повышенной сложности
П-5.1. Передаточная функция замкнутой системы имеет вид:
K(s)_ 96(.?+ 3)
74s) = -
R(s) (s + 8)(s2 + 8s + 3 6)
(а) Определите установившуюся ошибку при единичном ступенчатом входном воздействии, R(s) = 1/s.
(б) Полагая, что доминирующими являются комплексные полюсы, определите величину перерегулирования и время установления (по критерию 2% от установившегося значения).
(в) Получите график переходной характеристики исходной системы и сравните его с оценками, полученными в п. (б).
|
5440(t2s+1) |
|
а |
|
Y(s) |
|
s(s +28s+432) |
|
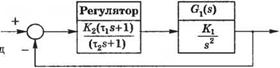
Рис. 5.2 (П). Система с варьируемым нулем |
|
К |
|||
|
s(s+2)(TpS+l) |
|||
|
система управления. Постройте графики реакции системы на единичное ступенчатое воздействие при хр = 0; 0,5; 2; 5. Представьте в виде таблицы показатели качества — относительное перерегулирование. время нарастания, время установления (по критерию 2%) для разных |
|
П-5.2. На рис. 5.2(П) изображена замкнутая система управления. Постройте графики _ реакции системы на единичное ступен- 0,5. Представьте в виде таблицы показа- ных значений т.. Проанализируйте влияние изменения т.. Сравните относительное положение П-5.3. На рис. 5.3(П) изображена замкнутая R(s) —V— , . " — - Y(s) |
|
Динамика поезда |
|
E(s) |
|
15 |
|
о |
|
R(s) |
|
К |
|
- r(s) Скорость |
|
(s+5)(s+7) |
|
Рис. 5.4 (П) Система управления скоростью |
|
Возмущение D(s) |
|
-6- |
значений т/г Проанализируйте влияние изменения тр. Сравните относительное положение полюса разомкнутой системы, lip, с положением полюсов замкнутой системы.
П-5.4. На рис. 5.4(П) изображена система управления скоростью пассажирского поезда-экспресса. Получите выражение для установившейся ошибки в зависимости от К при единичном ступенчатом воздействии КО-
(а) Вычислите установившуюся ошибку при значениях К, равных 1.10 и 100.
(б) Вычислите и изобразите графически реакции y(t) на (1) единичный ступенчатый сигнал r(lj и (2) на единичное ступенчатое возмущение d(t).
(в) Сведите в таблицу следующие показатели качества: относительное перерегулирование, время установления (по критерию 2%), е„ при отработке tit) и yld max для трех заданных значений К. Выберите наилучшее компромиссное значение К.
|
Рис. 5.5 (П) Система, в которой регулятор содержит параметр а |
|
Объект |
|
50(s+2) (s+3)(s+4) |
|
о~~ |
|
R(s) |
|
Y(s) |
|
Регулятор |
+ |
|
S+CX |
»( |
|
S |
+ |
|
о |
|
Возмущение D(s) |
П-5.5. На рис. 5.5(П) изображена система с регулятором, нуль которого может варьироваться. Пусть а = 0; 10; 100.
(а) Определите установившуюся ошибку при ступенчатом входном сигнале для и = 0 и и ф 0.
(б) Изобразите графически реакцию системы на ступенчатое возмущение для трех значений а. Сравните результаты и выберите наилучшее из трех значений а.
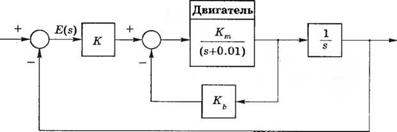
П-5.6. На рис. 5.6(П) изображена структурная схема двигателя постоянного тока, управляемого по цепи якоря.
(а) Найдите зависимость установившейся ошибки от параметров К, Кь и Кт в случае линейного входного сигнала, r(t) = t, t > 0.
|
|
|
R(s) |
|
Y(s) |
(б) Примите Кт = 10, Kh = 0,05 и выберите К так. чтобы установившаяся ошибка была равна 1.
(в) Вычислите и изобразите графически реакции системы на единичный ступенчатый сигнал и на сигнал, изменяющийся единичной скоростью, на интервале до 20 с. Являются ли эти реакции приемлемыми?
Задачи на синтез систем
СС-5.1. Система управления приводом скользящей части стола металлообрабатывающего станка (см. задачи СС-1.1-СС-4.1) подвержена возмущению за счет того, что обработка детали продолжается несмотря на удаление части материала. Регулятор представлен обычным усилителем Gc(s) = Ки. Оцените влияние единичного ступенчатого возмущения и определите наилучшее значение коэффициента Ка, при котором перерегулирование в случае ступенчатого задающего сигнала r(t) = A, t > 0, будет менее 5%, а влияние возмущения будет по возможности минимальным.
|
|
|
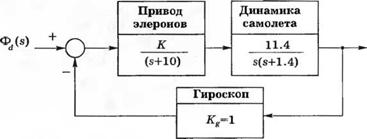
Рис. 5.1 (С) Система управления углом крена |
|
Ф(8) Угол крена |
С-5.1. На рис. 5.1(C) приведена система управления углом крена реактивного истребителя. Задача заключается в выборе коэффициента К, при котором реакция системы на ступенчатый входной сигнал ф(/) = A, t > 0, имела бы перерегулирование не более 20% и как можно меньшее время установления, (а) Определите передаточную функцию замкнутой системы Ф(.?)/<1/.$).
(б) Найдите корни характеристического уравнения при К = 0,7; 3; 6. (в) Используя понятие доминирующих корней, предскажите ожидаемое перерегулирование и время максимума переходной характеристики в аппроксимирующей системе второго порядка, (г) Постройте график реакции исходной системы и сравните показатели качества с полученными в п. (в), (д) Выберите значение К, при котором от носительное перерегулирование было бы равно 16%. Каково при этом время максимума?
С-5.2. При синтезе системы управления положением наконечника сварочного аппарата необходим тщательный подбор параметров. Такая система изображена на рис. 5.2(C), где С, = 0,2, а коэффициент К и собственная частота ы„ могут быть выбраны, (а) Найдите такие значения К и ы„, при которых реакция системы на единичный ступенчатый входной сигнал будет иметь время максимума (момент первого выброса за заданное значение, равное единице), не превышающее 1 с, и перерегулирование не более 5%. (Подсказка: попробуйте выбрать 0,1 < А7ш„ < 0,3.)
(б) Постройте график реакции полученной системы на ступенчатый входной сигнал.
|
Динамика руки с наконечником |
||
|
Усилитель и исполнительное устройство |
||
|
со? |
||
|
2L S |
s2+2^to„s+io^ |
|
-Ч> |
|
— y(s) Положение наконечника |
|
Рис. 5.2 (С) Система управления положением наконечника сварочного аппарата |
|
R(s). |
|
R(s) |
Рис. 5.3 (С)
Система
активной
подвески
автомобиля
О-
Задающий _ сигнал
|
Усилитель |
Электродвигатель |
|
|
К |
1 |
|
|
s(s+q) |
Y(s)
Положение
вентиля
С-5.3. Применяемые в современных автомобилях системы активной подвески обеспечивают комфортабельные условия при поездке. При синтезе таких систем используется идея настройки амортизаторов, приспосабливая их к дорожным условиям. Как показано на рис. 5.3(C), небольшой электродвигатель изменяет положение (проходное сечение) вентиля гидросистемы. Выберите значения параметров К и q, обеспечивающие наилучшее качество системы по критерию ИВМО при отработке ступенчатого задающего сигнала, причем время установления (по критерию 2%) при этом не должно превышать 0,5 с. Прежде чем завершить синтез, попытайтесь предсказать величину перерегулирования при ступенчатом входном сигнале.
|
|
Рис. 5.4 (С)
Система управления спутником
а)
|
б) |
|
|
|
R(s) |
|
Y(s) Угол ориентации |
|
Gc(s) |
G( s) |
|
|
К |
10 |
|
|
(s+90) |
(s+l)(s+9) |
С-5.4. Для изменения ориентации спутника, изображенного на рис. 5.4(C), (а), используется система управления, представленная на рис. 5.4(C), (б).
(а) Аппроксимируйте замкнутую систему моделью второго порядка.
(б) Используя модель второго порядка, выберите коэффициент К так, чтобы при отработке ступенчатого входного сигнала перерегулирование не превышало 15%, а установившаяся ошибка была менее 12%.
(в) Проверьте правильность синтеза, определив действительные показатели качества системы третьего порядка.
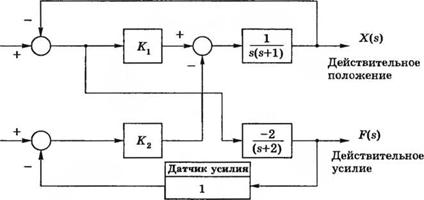
С-5.5. Для удаления заусениц с поверхности обработанных на станке деталей может быть использован робот, который перемещает инструмент по заранее заданной траектории, определяемой входным сигналом. На практике обычно возникают ошибки из-за неточности робота, погрешностей обработки, больших допусков и износа инструмента. Эти ошибки можно исключить, используя обратную связь по усилию, за счет чего траектория движения инструмента корректируется во время зачистки поверхности.
Хотя управление усилием в известной степени способно решить проблему точности, одновременно становится более трудным обеспечение устойчивости системы. Действительно, установив упругий датчик усилия на запястье руки робота и замкнув соответствующую обратную связь, мы напрямую сталкиваемся с проблемой устойчивости системы.
|
|
|
Желаемое положение |
|
Желаемое усилие |
|
Рис. 5.5 (С). Робот для зачистки поверхности деталей |
|
R(s) |
|
Рис. 5.6 (С). Система управления положением |
На рис. 5.5(C) изображена модель системы управления описанным выше роботом.
Определите область устойчивости системы в плоскости параметров и К2, считая, что оба они положительны.
С-5.6. На рис. 5.6(C) изображена система управления положением, в которой используется двигатель постоянного тока. Целью синтеза является выбор значений Ку и К2, при которых в случае ступенчатого входного сигнала время максимума переходной характеристики составляло бы 0,5 с, а перерегулирование было незначительным (от 0,5% до 2%).
|
Л ^ |
Кг |
||
|
s(s+l) |
|||
|
1+*2S |
|||
|
Y(s) |
Задачи, решаемые с помощью MATLAB
М-5.1. Замкнутая система имеет передаточную функцию
4
т=
s2 + 4s + 4
|
Получите импульсную переходную характеристику аналитически и сравните ее с результатом вычислений с помощью MATLAB (функция impulse). М-5.2. Система в разомкнутом состоянии имеет передаточную функцию см - ”7 |
|
R(s) |
s (s+ 10)
Считая, что система охвачена единичной отрицательной обратной связью, воспользуйтесь функцией Isim и получите реакцию замкнутой системы на линейный входной сигнал, R(s) = І/s2. Рассмотрите интервал времени 0 < t < 25 с. Чему равна установившаяся ошибка?
|
s2 +2£(o„s+(o^ |
|
-Y(s) |
М-5.3. Для синтеза систем управления очень важно твердо знать связь между расположением полюсов системы второго порядка, изображенной на рис. 5.3(М), и ее переходной характеристикой. Имея это в виду, рассмотрите следующие четыре случая:
(1) со,, = 2 , С = 0;
|
Л. |
Регулятор |
Объект |
|||
|
21 |
1 |
||||
|
S |
(s+2) |
||||
|
Y(s) |
(2) ш„=2,С = 0,1;
|
Д(з) |
(3) ш„ = 1 , С = 0;
(4) ю„ = 1 , С = 0,2.
|
Рис. 5.4 (М). Система управления с отрицательной обратной связью |
С помощью функций impulse и subplot создайте в окне на экране монитора четыре диаграммы, каждая из которых соответствовала бы импульсной переходной характеристике для указанных выше случаев. Сравните диаграммы с изображенными на рис. 5.17 в разделе 5.6 и проанализируйте результаты.
М-5.4. Рассмотрите систему управления, изображенную на рис. 5.4(М).
(а) Покажите аналитически, что при ступенчатом входном сигнале переходная характеристика замкнутой системы имеет перерегулирование около 50%.
(б) С помощью MATLAB получите график реакции системы на ступенчатый входной сигнал и оцените по нему величину перерегулирования. Сравните результат с предсказанным в п. (а).
М-5.5. Передаточная функция прямой цепи в системе с единичной отрицательной обратной связью имеет вид:
50
GO) =------------ .
*0+10)
С помощью MATLAB постройте переходную характеристику замкнутой системы и определите по графику приблизительные значения ее максимума, Мр, времени максимума, Тр, и времени установления, Ts (по критерию 2%). Дополните график соответствующими численными значениями Mjr Тр и 7(.
М-5.6. Для удержания самолета на заданном курсе и высоте обычно используется автопилот. Система управления в данном случае имеет вид рис. 5.6(М).
(а) Предположим, что регулятор представлен обычным коэффициентом усиления, т. е. Gc(s) = 2. С помощью функции Isim вычислите и постройте график реакции системы на воздействие 0(//) = а/, где а = 0.5 °/с. Определите ошибку по положению спустя 10 с.
(б) Если взять более сложный регулятор, то можно уменьшить установившуюся ошибку при отработке входного сигнала. С этой целью выберем регулятор с передаточной функцией
Gc(s) = K, + ^ = 2+- .
S S
|
|
Регулятор такого типа известен как пропорционально-интегральный (ПИ) регулятор. Повторите для такого регулятора те же действия, что и в п. (а), и сравните установившиеся ошибки.
-Л
Желаемое
положение
|
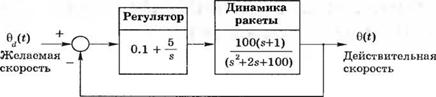
Рис. 5.7 (М). Система управления скоростью ракеты |
М-5.7. На рис. 5.7(М) изображена структурная схема системы управления скоростью ракеты. С помощью известных формул для системы второго порядка предскажите значения показателей Мр, Тр и Тч для замкнутой системы в случае единичного ступенчатого входного сигнала. С помощью MATLAB получите точную реакцию исходной системы и сравните показатели качества с предсказанными по упрощенной модели. Объясните возникшие различия.
Ключевые термины и понятия
Время максимума. Момент времени, в который реакция системы на ступенчатый входной сигнал достигает максимального значения.
Время нарастания. Время, в течение которого реакция системы на ступенчатый входной сигнал становится равной определенной процентной доле от величины входного сигнала. Время нарастания Т,- определяется изменением выходной переменной от 0 до 100% величины входного сигнала. Как альтернатива, время нарастания Тт определяется изменением выходной переменной от 10% до 90% ее установившегося значения.
Время установления. Время, в течение которого выходная переменная системы устанавливается в пределах определенной процентной доли от величины входного сигнала.
Доминирующие корни. Корни характеристического уравнения, в основном определяющие вид переходной характеристики системы.
Коэффициент ошибки по скорости Kv. Коэффициент, вычисляемый как 1ітЛ_>о[іС(і)]. Установившаяся ошибка системы при линейном входном сигнале, изменяющемся со скоростью А. равна AIKV.
Оптимальная система управления. Система, параметры которой настроены так, что оценка качества имеет экстремальное значение.
Оценка качества. Количественная мера качества системы.
Перерегулирование. Величина, на которую реакция выходной переменной превышает желаемое значение.
Тестовый входной сигнал. Входной сигнал типового вида, используемый для проверки способности системы реагировать адекватным образом.
Тип системы. Число N полюсов передаточной функции G(s), расположенных в начале координат, где G(s) соответствует разомкнутой системе (прямой цепи от входа к выходу).
Требования, выдвигаемые при синтезе. Набор заранее установленных критериев качества.