Спектральные и временные характеристики оптических параметрических генераторов
Оптическая параметрическая генерация (ОРО) имеет много общего с лазерной генерацией. В обоих случаях обратная оптическая связь, обусловленная зеркалами, приводит к генерации и устанавливает условия для амплитуды усиления по отношению к резонаторным потерям и резонаторным длинам волн. В этом разделе мы сконцентрируем наше внимание на двух аспектах, которые специфичны для ОРО, а именно их спектры усиления и динамические характеристики.
|
(12.Г.1) |
![]() Параметрическое усиление определяется геометрическими факторами применительно к условию фазового согласования, что контрастирует с лазерами, где усиление имеет место через квантовые переходы, происходящие с участием дискретных атомов или в пределах зонной структуры кристалла. Именно из-за этого ОРО являются исключительно полезными в качестве перестраиваемых когерентных источников излучения для спектроскопических исследований атмосферы, биологии и т. д. Уравнение (12.33) показывает, что эффективность преобразования для параметрического процесса такого, как со3 -» сох + со2 зависит от фазового рассогласования А к =к2 — к{ — к2 и пропорциональна sinc2(A/:L/2), где L есть длина нелинейного материала. Таким образом, полуширина кривой усиления (т. е. спектральная восприимчивость) дается выражением:
Параметрическое усиление определяется геометрическими факторами применительно к условию фазового согласования, что контрастирует с лазерами, где усиление имеет место через квантовые переходы, происходящие с участием дискретных атомов или в пределах зонной структуры кристалла. Именно из-за этого ОРО являются исключительно полезными в качестве перестраиваемых когерентных источников излучения для спектроскопических исследований атмосферы, биологии и т. д. Уравнение (12.33) показывает, что эффективность преобразования для параметрического процесса такого, как со3 -» сох + со2 зависит от фазового рассогласования А к =к2 — к{ — к2 и пропорциональна sinc2(A/:L/2), где L есть длина нелинейного материала. Таким образом, полуширина кривой усиления (т. е. спектральная восприимчивость) дается выражением:
AkL = ±п
При точном согласовании фаз фотоны в коллинеарной геометрии удовлетворяют двойным условиям сохранения как энергии, так и импульса:
|
|
(12.Г.2)
А К _ пз(лз) и, (Л,) и2(Д,) _ 0
2л Л, Л, А?
В этом последнем уравнении мы не уточнили тип использованного фазового согласования. Это может быть конфигурация типа е -» о + о, в случае которой пъ = я,(Л3), п{ = по(Лх) и п2 = по(Л2) или это может быть конфигурация другого типа. Более того, в случае квазифазового согласования с периодом А к уравнению фазового согласования должен быть добавлен волновой вектор 2л/А. Таким образом мы будем искать, какое влияние на вектор А к будут оказывать изменения АЛг При фиксированной длине волны Л3 изменения сигнальной и холостой волн связаны через производную первого уравнения в (12.Г.2):
|
АЛ1 _ АА, Влияние рассматриваемого фактора на фазовое рассогласование может быть выявлено дифференцированием второго уравнения в (12.Г.2): |
|
(12.Г. З) |
|
DЯ1 Я| dЯ9 С учетом (12.Г.1) и (12.Г. З) это последнее уравнение приводит к полуширине кривой усиления: |
|
D«, AAj d«2 АД2 |
|
А к 2 к |
|
= -^-АЛ, + Л ' |
|
(12.Г.4) |
|
А 3 Л23 2 |
 |
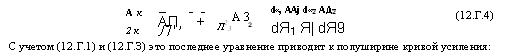 |
|
V1 |
|
3L L |
|
Dn2 DlT |
|
П - п, + |
|
|
|
|
|
|
Спектральная восприимчивость ОРО
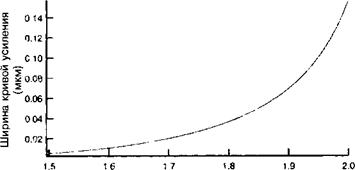
Отметим, что чем ближе мы приближаемся к условию вырождения (т. е. со{ ~ о)2), тем шире будет кривая усиления. Такой характер иллюстрируется следующим ниже примером, а также рисунком 12.Г.1. В ряде случаев желательно добиться максимально узкой кривой усиления (как например в случае одномодовых ОРО). В этом случае становится необходимым использовать конфигурации с различными поляризациями сигнальной и холостой волн (т. е. конфигурации типа е -» е + о, называемые параметрическими взаимодействиями второго рода). В том случае, когда поляризации сигнальной и холостой волн идентичны, такой случай относится к типу I.
Пример-----------------------------------------------------------------------
С учетом кривых Зеллмайера для ниобата лития, приведенных в дополнении 12.Б, приведенная ниже программа позволяет рассчитать зависимость ширины полосы от длины волны сигнала при длине волны накачки 1,064 мкм.
Ае=4.5820;Ье=0.099169;ce=0.044432;de=0.0211950; ao=4.9048;bo=0.11768;co=0.04750;do=0.027169; ne2[IJ:=ae-be/(ce-r2)-de*r2;ne[IJ:Sqrt[ne2[l]]; Ip=1.062;l2=1./(1./Ip-1./I1);
L= 104;
Dn[l_]=1, no[l];
АЛ = Abs ^-(по[11] = no[l2] + dn[l2]l2 - dn[H]M)-1 Plot[AX, {11,1.5,2}]
Таким образом, разрешенные резонаторные моды в ОРО, попадающие в контур спектра усиления нелинейного кристалла, будут испытывать усиление. При этом, отклик ОРО будет жестко зависеть от типа резонанса внутри резонатора.
Первый случай затрагивает ОРО, в котором резонансна только сигнальная волна а)х (т. е. в данном случае имеет место случай ОРО с одиночным резонансом, или случай 8ЛОРО, иллюстрируемый рисунком 12.Г.2). Усиливаются все разрешенные частоты У1т = тс/2пхЬса^ разделенные свободным спектральным интервалом (АуР8К = с/2л,//сау), что соответствует числу мод А^=2(АД1/Д1)(/,сауД1), способных принимать участие в генерации. Принимая АЯ, = 0,01 мкм, А, =1,6 мкм и Ьсау = 4 см, получаем, что число разрешенных мод составляет 312. В режиме непрерывного функционирования (непрерывный ОРО) из-за конкуренции мод (смотрите дополнение 13.Д) будет генерироваться лишь одна мода, наиболее близкая к пику кривой усиления. В этом случае перестройка частоты возможна за счет изменения длины резонатора. Частота генерации изменяется линейно и непрерывно со смещением резонаторных мод вплоть до того момента, когда прилегающая мода не станет наи-
|
Длина волны сигнала (мкм) Рис. 12.Г.1. Зависимость кривой длины усиления при параметрической генерации в нистате лития с длиной волны накачки 1,069 мкм. |
Более близкой к максимуму кривой усиления. Когда это происходит, колебания «перескакивают» на соседнюю моду (что является типичным для ОРО в непрерывном режиме (смотрите рис. 12. Г.2)). Таким образом эффективный диапазон точной перестройки равен свободному спектральному интервалу.
В дважды резонансном ОРО (ЭЛОРО) моды определяются двумя условиями:
• со2 = + со2
• собственные моды со1т и а)2т перекрываются контуром кривой усиления ОРО.
Эти два условия могут быть представлены в виде диаграммы Джиордмэйна— Миллера (смотрите рис. 12.Г. З). Оси частот сигнальной и холостой волн ориентированы в противоположных направлениях и располагаются таким образом, чтобы любая пара частот со1т и со2т на одной вертикальной линии складывались, чтобы дать частоту накачки соу Таким образом, будут способны генерировать лишь те пары мод (°т и которые перекрываются в пределах их соответствующей ширины линии (Ао). = Д*ур8К//], где / = 1,2, а Р. есть зеркальность резонатора на частоте (о). С учетом дисперсии нелинейной среды зазор между модами соХт и со2т будет изменяться в зависимости от частоты, и лишь немногие моды будут способны перекрываться в пределах кривой усиления (даже в импульсных условиях — смотрите рис. 12.Г. З). Таким образом, ЭЛОРО по своей природе более благоприятствует одномодовой генерации по сравнению с 8 ЛОРО. С другой стороны, эти приборы имеют тенденцию быть менее стабильными. Одной из причин такой нестабильности является эффект группирования мод. Если кривая усиления достаточно широка (что часто имеет место!), то пара несоседних резонаторных мод может оказаться более близко
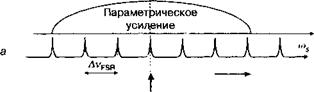
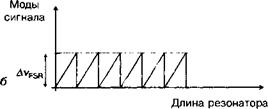 Рис. 12.Г.2. Спектральная перестройка SROPO: все моды, лежащие внутри контура кривой усиления способны к генерации. В режиме непрерывной генерации генерирует лишь мода, ближайшая к максимуму кривой усиления (а). Изменение длины резонатора обеспечивает частотную перестройку в пределах свободного спектрального интервала.
Рис. 12.Г.2. Спектральная перестройка SROPO: все моды, лежащие внутри контура кривой усиления способны к генерации. В режиме непрерывной генерации генерирует лишь мода, ближайшая к максимуму кривой усиления (а). Изменение длины резонатора обеспечивает частотную перестройку в пределах свободного спектрального интервала.
|
|
|
|
|
|

-I___ > > 1м > і___ і.,-- 1 I U
Длина резонатора
Расположенной, чем пара соседних мод (смотрите рис. 12.Г. З). В этом случае частота генерации будет флуктуировать между этими двумя модами, что приведет к нестабильности выходных характеристик ОРО.
Как правило, параметрическое усиление в нелинейном кристалле достаточно слабо и линейно увеличивается с ростом уровня накачки. Таким образом, очень выгодно использовать ОРО в импульсном режиме, когда для накачки нелинейного кристалла используются импульсы с высокой пиковой интенсивностью (например, генерируемые лазером с переключением добротности). В связи с этим приступим к описанию переходных характеристик ОРО в импульсном наносекундном режиме, т. е. режиме, когда длительность импульсов соответствует времени жизни резонаторных фотонов.
Для этой цели попробуем описать эволюцию амплитуд различных волн в процессе обращения фотонов в резонаторе (в промежутке между tn и tn+ ,). Более того, сделаем следующие допущения:
• Относительные фазы волн таковы, что константа движения в пределах структур Г = 0, т. е. cos 0=0. Это означает, что различные фазы остаются постоянными в нелинейном кристалле (смотрите (12.В.9)).
• Предполагается, что параметрическое усиление достаточно слабо настолько, что (12.В.9) может быть линеаризовано.
|
' L_ 2 |
![]() При этих двух допущениях (12.В.9) может быть записано в виде:
При этих двух допущениях (12.В.9) может быть записано в виде:
' L_
2
<(!)= И"
|
KL, + —". |
|
U"(L)= и" |
|
2 V ' L 2 |
|
KL |
|
«,'(£)= «3 |
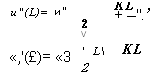 |
|
|
|
В ОРО волны в), направляются в обратном направлении зеркалами с полным коэффициентом отражения г. (который временно предполагается действительным) ко входу резонатора так, что новые входные сигналы в моменты времени іп + 1 равны:
|
KL, + —wi |
|
L_ 2 |
|
|
Здесь: Л0 есть накачивающее электрическое поле на входе ОРО. В момент времени
І амплитуды волны посередине нелинейного кристалла в этом случае составляют:
|
+ 0 + Г| )"уМ2 |
![]() = <+'(0)+y-«2"(y
= <+'(0)+y-«2"(y
|
|
||
|
|||
|
|||
|
|||
Введем теперь новое обозначение я.(/я) = и. п(Ь/2). В этом случае приращения амплитуды различных волн в процессе кругового обращения в резонаторе составляют:
|
(12. Г. 9) |
![]()
|
D / |
![]() АкУкТ = «Г1
АкУкТ = «Г1
Здесь: Гкт есть время кругового обращения в резонаторе, т. е. Тят = 2Ь/с. В этом случае уравнение (12.Г.6) может быть записано в виде:
TOC o "1-5" h z d^ г,
±а2(()=-^+та3 (12.Г.10)
О/ 7*2
4-° Л0= АО - — - паіа2
А/ г3
Динамические уравнения ОРО
Эти уравнения описывают динамическое поведение ОРО. В этом случае различные величины, присутствующие в (12.Г.10) даются выражениями:
1-і-//
Г Твт
(12.Г.11)
КС
У, =(1 + ^)
Величины а. являются действительными волновыми амплитудами посередине нелинейного кристалла, связанные с фотонными потоками через соотношение (12.37), т. е. Ф. = af/2hZ0. Эти величины, однако, могут быть отрицательными (что соответствует 0= —л/2 в (12.В.9)), поскольку они описывают колебательный перенос энергии между различными модами в процессе их взаимодействия в нелинейном кристалле. Здесь ДО представляет член источника накачки ОРО (по амплитуде), у. представляют собой различные нелинейные члены связи, а г. — времена жизни фотонов с различными частотами в резонаторе.
Для детального описания однорезонансного ОРО (SROPO) мы должны сделать предположение о том, что обратная связь по отношению к сигнальной и холостой вол-нам отсутствует так, что г2 = г, = 0. В (12.Г. 10) время жизни для холостой волны может считаться пренебрежимо малым по сравнению с сигнальным временем жизни (г, = Ткт/( — г,) и продолжительностью импульса накачки, которое, как правило, составляет несколько наносекунд. Это аналогично тому, что dajdt — 0 так, что:
^aXt)=~—+ у? а2а, at Tj
|
(12.Г.12) |
![]() А2 = 8гааъ
А2 = 8гааъ
■4«з(0=/(0- —-Гз«,а2 at тъ
Динамические уравнения SROPO
При этом g2 = kL/2.
Теперь представляет интерес решить (12.Г. 10) в общем случае (SROPO, DROPO) для стационарных условий, т. е. при const и da./dt= 0. Уравнение (12.Г.10)
Приводит к:
|
(12.Г.13) |
![]() А^~Г^у2т2а])=0
А^~Г^у2т2а])=0
Г аъ
/ = — + Угааг т,
3
Как и в случае лазерных уравнений (4.34) и (4.35), это уравнение допускает два типа решений:
• Ниже порога. Фотонные потоки сигнальной и холостой волн равны нулю (а1 = а2 = 0), а амплитуда потока фотонов накачки в резонаторе возрастает линейно в функции амплитуды накачки (а3 =/г3).
• ![]() Выше порога. Фотонный поток накачки фиксируется на своем пороговом значе - НИИ, определяемом А} 1ЪгаНои = а321|1геЛоИ = 1/(у1г1у2г2). Фотонный поток сигнальной волны определяется вторым уравнением (12.Г. 13):
Выше порога. Фотонный поток накачки фиксируется на своем пороговом значе - НИИ, определяемом А} 1ЪгаНои = а321|1геЛоИ = 1/(у1г1у2г2). Фотонный поток сигнальной волны определяется вторым уравнением (12.Г. 13):
(12.Г.14)
Здесь: порог задается выражением /1Ьге8ЬоШ = а31Нге8Но1аА3. Это означает, что пороговая мощность накачки ЭЛОРО пропорциональна 1/Т{Т2, где Т. — коэффициент пропускания зеркала, который мы уже определили (12.62).
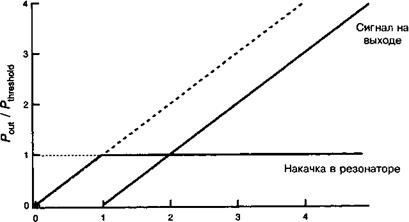
Уравнение (12.Г. 14) предполагает также, что мощность выходного сигнала Рх пропорциональна у1Р3/Р3 ,Ьге$Ьо1с1 “ 1? как это иллюстрируется рисунком 12.Г.4. Эта зависимость явно отличается от линейной зависимости Р. п — Рои{ для лазеров. Этот момент, как правило, опускается многими аваторами, и он будет более детально обсуждаться в дополнении 12.Е.
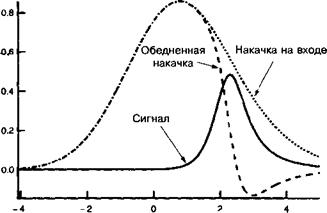
Следующий ниже рисунок 12.Г.4 иллюстрирует временную эволюцию ЭЯОРО, как это описывается выражением (12.Г. 10). Рисунок 12.Г.5 показывает временную эволюцию накачивающей волны на выходе резонатора ОРО, полученную исходя из этих уравнений. Начиная с уровня параметрического флуоресцентного шума, сигнальная волна возрастает экспоненциально, при этом сигнальная и холостая волны быстро истощают мощность пучка накачки.
Пример
Исследуем временную эволюцию ОЛОРО, накачиваемого импульсами гауссовской формы. Уравнения нормированы и решены с использованием программы МАТНЕМАТ1СА. Мы видим, что сигнал не может возрастать без предварительной «затравки» малым количеством фотонов источника, поставляемых параметрической флуоресценцией.
G=5;t=2;eq1 = ар’[ t ]= = E (t/t> — ap[t] - g as[t] ac[t]; eq2 = as’ [t] = = - as[t] + g ac [t] ap [t]; eq3 = ac’ [t] = g as[t] ap[t];
Sol = NDSolve[{eq1, eq2,eq3, ap[-5] = = 0, as [-5] = = 0.001, ac [ -5] = = 0.001},
|
Накачка на входе
V Pin / threshold Рис.12.Г.4. Отклик ОРО в функции квадратного корня от мощности накачки. |
|
Интенсивность (отн. ед.) |
![]() Рис. 12.Г.5. Временной профиль амплитуд накачивающей и сигнальной импульсных волн в ОРО, полученный с использованием уравнений связан - Время " ныхмод (12.Г.10).
Рис. 12.Г.5. Временной профиль амплитуд накачивающей и сигнальной импульсных волн в ОРО, полученный с использованием уравнений связан - Время " ныхмод (12.Г.10).
{ap[t]f as [t], [ас [t]}, {t, -5,5}];
P1 = Piot[Evaluate [t]/. sol, {t,-5,5}],
PlotStyle ®RGBcolor [1, 0, 0], DisplayFunction ® Identity];
P3 = Plot[Evaluate[as [t] /. sol, {t, — 5,5}], PlotStyle ® RGBColor[0, 0, 1], DisplayFunction ® Identity];
J. A. Giordmaine and R. C. Miller, Phys. Rev. Lett. 14, 973 (1965). Y. S. Shen, The Physics of Nonlinear Optics, Wiley, New York (1984).