Оптоэлектроника

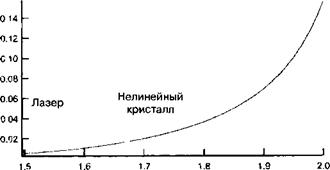
Параметрические взаимодействия в лазерных резонаторах

Как следует из (12.33) или (12.68) эффективность параметрического преобразова­ния пропорциональна интенсивности пучка накачки. Таким образом, было бы вы­

Годно, чтобы параметрическое взаимодействие могло иметь место в оптическом резонаторе самого накачивающего лазера, поскольку интенсивность пучка накачки в 1 /Т раз (где Т пропускание зеркала) больше выходной мощности накачки (смот­рите дополнение 9.Г.) В связи с этим исследуем эффективность внутрирезонатор - ного преобразования частоты. Для того, чтобы упростить наш подход и выделить наиболее важные аспекты рассматриваемой проблемы, предположим, что:

1. Соображения согласования фазы были учтены адекватным выбором резона­тора, что позволяет нам сфокусировать наше внимание исключительно на числе фотонов в резонаторе.

2. Амплитуды волн в резонаторе не зависят от положения: эта аппроксимация представляется разумной в том случае, когда зеркальность резонатора на частотах со и 2со больше нескольких единиц.

3. Вся среда характеризуется одним коэффициентом преломления, что позво­ляет пренебречь влиянием вариации эффекта преломления.

Разработаем теперь формализм для внутрирезонаторного удвоения частоты. Необходимая для этого конфигурация эксперимента и соответствующие обозначе­ния иллюстрируются рисунком 12.Д.1. Предположим, что параметрическое усиле­ние достаточно слабо с тем, чтобы оправдать аппроксимацию необедненного пучка (смотрите раздел 12.3). В течение временного интервала с1/ энергия Рш и Р2(о, содер­жащаяся в (о - и 2(0-волнах, покидающих нелинейную среду, связана с числом фото­нов Р2 на частоте 2а) и Рх на частоте а) следующими соотношениями:

С'&

(12.Д.1)

.

'2 51

Здесь с! — скорость света в среде, 5 — сечение пучка по нормали, а Ь — полная длина резонатора. Скорость изменения числа фотонов из-за нелинейного взаимо­действия, определяется соотношениями:

(12.Д.2)

= - Кп, Рг

ПІ* 1

N1-

Здесь, как мы напоминаем, для генерации одного фотона с частотой 2а) необходи­мы два фотона с частотой а). Напомним, что для того, чтобы найти выражение для Кпі, с одной стороны, мощность циркулирующая по резонатору и скорость обмена числом фотонов связаны соотношением:

Pl•= ^siiPl2hco = ^sLp? h0} (12-д.3)

С другой стороны, интенсивности Рю и Р2(о определяются (12.33):

Р2ь = чК (12.Д.4Л)

Здесь г] — эффективность преобразования (в м2 Вт-1):

П = 2-^-(we0x2Lniy (12. Д.46)

П1П2(ь

В пренебрежении обеднением пучка накачки в кристалле коэффициент Кп[ по­лучается из (12. Г. З) и (12.Г.4):

K’"=T}Wnco (12'Д'5)

Обратим теперь наше внимание на реакцию внутрирезонаторной лазерной среды. Временная эволюция среды в отсутствие эффекта удвоения частоты определя­ется (4.34) и (4.35), при этом мы должны учитывать, что лазерная среда занимает лишь часть резонатора.

±N =r2(N0-N)-К, МР,

Dt (12. Д.6а)

А/> = K, NPt -

Здесь: N — число атомов в состоянии инверсной заселенности, а К. — коэффици­ент линейной связи:

К,=Ц*- (12. Д.66)

В отсутствие какого-либо параметрического взаимодействия мы немедленно приходим к стационарному поведению системы. Если число атомов N меньше по­роговой величины A^threshold, то число фотонов Рх будет равно нулю и N = N0 (пропор­ционально мощности накачки). В противоположной ситуации Добудет фиксирова - но на уровне JVthreshold:

Г

^ threshold “ ts

^ = --—------------------------------------ (12. Д. 1а)

I ^ ^"op^cavl

При этом число фотонов Рх будет даваться соотношением:

Р, = Рш(г~ О (12.Д.76)

Здесь: Psat = Г2/К1 = SL/ccro т2 есть число фотонов насыщения, а г — нормированная

Скорость накачки г = Nthreshoid (смотрите раздел 4.6), теперь нам остается только

Свести вместе эти два механизма (усиление и преобразование частоты) для того, чтобы описать процесс в резонаторе:

-^N =T2(N0-N)-K, NPi Л-Р^КМ-Г^-К^ (12.Д.8)

— Р — V Р2 _ Г Р

^ Г2 - 2 Лп1г1 сэу2 2

В стационарном состоянии второе уравнение системы дает возможность уста­новить связь между числом инвертированных атомов с числом фотонов Рх:

= НХЫМА + рРх (12.Д.9в)

При этом:

(12. Д.96)

*1

Таким образом, инверсная плотность более не является фиксированной! Это происходит из-за того, что фотоны с частотой со не насыщают лазерные переходы, т. к. они устраняются из резонатора за счет превращения в фотоны с частотой 2со. При подстановке (12.Д9) в первое уравнение (12.Д.8) число фотонов Рх будет да­ваться решением квадратного уравнения:

И[(г-і)-/7Г]=(і + /7Г)Г (12.Д.10)

Здесь: есть отношение и = Г2/Гсау1 и К= Р,/Л^ге8Ьо1а (смотрите (4.36)). Число фотонов

Г 2Р2, покидающих резонатор, в этом случае дается третьим уравнением системы

(12.Д.8), т. е.:

Г,„2Л =%^Ко, а^2 (12.Д.11)

2

4( +ирУ +4ир(г-1) - (1 + и/ЗУ

* я (12 Д12)

К, ъир

Эта последняя величина существенно зависит от параметра и(3= Ап1/(Гсау1А’//Г2), который представляет собой ничто иное, как нелинейный параметр, нормирован­ный на линейные параметры. Анализ (12.Д.12) показывает, что коэффициент нели­нейности Кп1 можно выбрать для достижения оптимальной эффективности и это для каждого уровня накачки г; достаточно, чтобы и/3 = 1т. е. при коэффициенте нелинейности, определяемом соотношением:

Кор, Рт = гса> , (12.Д.13)

Это последнее уравнение показывает, что оптимальный уровень нелинейной связи имеет место, когда нелинейные потери при насыщении (^ Р^) соответству­ют линейным резонаторным потерям. Таким образом, мы видим, что представляет интерес минимизация линейных потерь для того, чтобы свести к минимуму длину нелинейного кристалла. Оптимальный поток фотонов с энергией 2со, который мо­жет покинуть резонатор, составляет:

Г«* 2 Л = - , Рш (>/Г - 1 )2 (12.Д. 14)

2

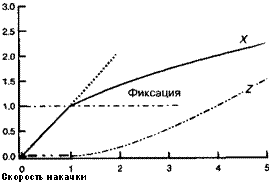
Заметим, что этот поток пропорционален (л/г —1)2;за пределами порога ос­новная часть энергии накачки преобразуется в фотоны с частотой 2со, при этом поток фотонов с частотой 2со становится пропорциональным V/*. Таким образом, резонатор ведет себя практически как идеальный преобразователь частоты. Ри­сунок 12.Д.2 показывает изменения нормализованной инверсной заселенности X = А7Л^Ьге8Ьо1(1 и нормированного потока Z = Р2/^Ьге8Ьо1а фотонов с частотой 2со в функции скорости накачки г. На этом рисунке четко видны уход от состояния фиксации инверсной заселенности X, а также зависимость вида (у1г — I)2 числа фотонов Z с частотой 2со.

Временная зависимость сигнала, полученная с помощью (12.Д.8) и в пренебре­жении членом спонтанной эмиссии Г2(А^0 — ТУ) во время импульса, может быть записана в виде:

— X =-ЛУ

(1/

Г Р -

1 СЯУ 2 1 2

Рис. 12.Д.2. Изменение нормиро­ванного числа атомов усиливающей среды в возбужденном состоянии X, а также нормированного фотонно­го потока Z с частотой 2со в функ­ции скорости накачки г.

-j-Z = 4гуг dt 2

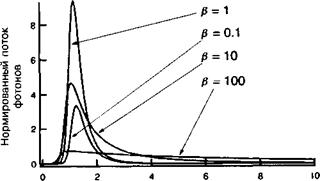
Рисунок 12.Д. З демонстрирует временную зависимость фотонного потока с ча­стотой 2а), полученную с использованием дифференциальных уравнений (12.Д. 15). Как и ранее (смотрите раздел 4.6.2), в рассматриваемом случае необходима «затрав­ка» для стимулирования эффекта спонтанного излучения (параметрической флуо­ресценции). Рисунок 12.Д. З демонстрирует также, что в случае большой величины коэффициентов связи (Я> 1) длительность импульсов становится большой, но при этом интегральная величина (энергия импульса) остается неизменной. Это — хоро­шая новость: она означает, что малые нелинейности тонких нелинейно-оптических кристаллов достаточны для обеспечения хорошей SHG-эффективности. И в дей­ствительности, внутрирезонаторные SHG на длину волны 1,06 мкм с использова­нием лазера на основе YAG стали подлинной «рабочей лошадкой» современных мощных лазеров видимого диапазона, которые смогли полностью заменить ионные газовые лазеры.

Пример----------------------------------------------------------------------------------------------------------------------------------------------------

Приведенная ниже программа MATHEMATICA дает расчет импульсного процесса, описываемого (12.Д.15).

Xi=10; b =1;

Eq1=y [t] = = y[t]*(x[t]-1)-b у[Г2; eq2=x[t] = =-x[t]*y[t];

Soh=NDSoive[{eq1,eq2,x[0] = = xi, y[0] = = 0.001 },{x[t],y[t]},{t,0.,50}]; plot2=Plot[Evaluate[b y[t]''2/sol,{t,0,50}],Plotstyle-> {RGBCoior[.5,0,.5]},PiotRange->{0,1},DispiayFunction->identity];