Обеднение накачки при параметрических взаимодействиях
Во время нашего рассмотрения параметрического взаимодействия в главе 12 предполагалось, что эффективность преобразования между пучком накачки, с одной стороны, а также сигнальной и холостой волнами, с другой стороны, настолько
низка, что мы можем пренебречь любым ослаблением интенсивности пучка накачки (т. е. как предполагалось в разделе 12.3, Е(z) = Е0). В действительности же в настоящее время для некоторых ОРО-материалов реальным является уровень эффективности, превышающий 50%. Поскольку энергия должна сохраняться в процессе параметрического взаимодействия, возникновение нелинейных волн должно происходить за счет энергии пучка накачки. Однако точное описание ослабления интенсивности пучка накачки требует более точного учета параметрических взаимодействий. Наиболее примечательным является то, что по мере рассмотрения материала этого раздела мы обнаруживаем первичную роль, которую играют в параметрических взаимодействиях относительные фазы различных волн. В главе 12 этот аспект проблем был априори недостижим из-за нашей начальной посылки упростить задачу за счет аппроксимации постоянного уровня пучка накачки.
Наше рассмотрение мы начнем со случая согласованного по фазе (Ак = 0) процесса генерации второй гармоники (со + со = 2со):
|
-А,., = - i кАшА2<0 |
![]() _а Dz
_а Dz
Й (12. В. 1а)
— А2„ = -кА1 dz
|
V/2 (12.В.16) |
![]() Как мы напоминаем, здесь: к есть параметр нелинейной связи, определяемый выражением:
Как мы напоминаем, здесь: к есть параметр нелинейной связи, определяемый выражением:
2(0
П1П 2«
2 с
Для учета фазовых эффектов введем переменные:
|
(12.В.2) |
![]() А» = «iei6'
А» = «iei6'
А2л = м2е‘в-’
После подстановки в (12.В.1) и приведения подобных членов мы приходим к системе связанных дифференциальных уравнений:
— щ = ки{и2 sin (02 - 20,) d z
— и2= ки2{ sin(20, - 02)
Dz (12.B.3)
— в, = - ки2 cos(в2 -20,) dz
— в2 = - к —cos(20, - в2)
Dz И2
Эти уравнения могут быть существенно упрощены, если будут найдены их инварианты (или константы движения). Первый инвариант получается из комбинации первых двух уравнений (12.В. З), что дает:
U{(z)2 + w2fe)2 ~ul - const (12.B.4)
Это выражение есть ничто иное, как выражение закона сохранения энергии.
Второй инвариант получается делением уравнений по du./dz на уравнения по dO./dz и введением члена относительной фазы 0= 20, — 02, что дает:
D щ щ
Leo.»
|
(12.В.5) |
![]() D и2 и,
D и2 и,
Эти два уравнения (12.В.5) могут быть скомбинированы с тем, чтобы получить одно уравнение:
|
(12.В.6) |
![]() W,2(z)w2(z)cos 0(0= «i2(0)w2(0)cos ^Ф)= г
W,2(z)w2(z)cos 0(0= «i2(0)w2(0)cos ^Ф)= г
Здесь Г есть константа, определяемая граничными условиями. Это последнее уравнение показывает, каким образом в процессе нелинейного взаимодействия в кристалле изменяется разность фаз между двумя волнами. Если предположить, что начальная амплитуда волны второй гармоники на входе нелинейного кристалла равна нулю (т. е., что амплитуда обратной связи равна нулю), то м2(0) = 0 и константа Г равна нулю. При z > О (12.В.6) удовлетворяется для ненулевой падающей волны, если только 9(z) = const = (2т + )л/2. В этом случае и0 в уравнении сохранения энергии есть амплитуда волны накачки на входе нелинейной среды, при этом уравнение для амплитуды u2(z) принимает вид:
— и2 = к(и1 - и]) (12.В.7)
D Z
Уравнение (12.В.7) может быть легко проинтегрировано, что дает эволюцию амплитуды в нелинейной среде:
SHAPE \* MERGEFORMAT ![]()
|
W2fe) = иоtanh Здесь: £ есть длина преобразования частоты: |
![]()
|
3/2 |
![]()
|
£ _ 1 _ с п |
![]() (12.В.80)
(12.В.80)
Длина преобразования частоты
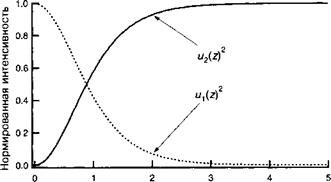
Здесь: п~пш~ п2(о, /есть мощность падающего излучения, а Z0 — вакуумный импеданс (377 Ом). Рисунок 12.В. 1 демонстрирует изменение нормированной интенсивности (м,/м0)2 и (и2/и0)2 в функции нормированного расстояния z|&
Заметим, что после распространения на расстояние, примерно равное длине преобразования, 50% энергии волны накачки будет преобразовано в излучение второй гармоники.
|
Нормированное расстояние Рис. 12.В.1. Эволюция нормированной интенсивности волн накачки и второй гармоники в функции расстояния распространения, нормированного на длину преобразования в нелинейной среде. |
Рассмотрим кристалл с нелинейной восприимчивостью 10 пм В-1 коэффициентом преломления 1,5. Мощность падающей волны на длине волны Л = 1 мкм составляет 10 кВт в пределах площади 1 мм2. В этом случае уравнение (12.В.86) дает:
|
(12.В.8*) |
|
П |
|
3/2 |
|
'т |
|
Л, |
|
|
![]()
![]()
Рассмотрим теперь более общий случай, затрагивающий трехволновое параметрическое взаимодействие со3 = со{ + сог Исходя из (12.38) и обобщая предыдущую замену переменных (т. е. Ак = ик&вк),получаем следующую систему связанных нелинейных уравнений:
С1 . а
---- их - КЩЩ 81П в
—
|
(12.В.9) |
![]() Щ = - кижьтв dz
Щ = - кижьтв dz
|
<$1 их |
|
|
|
|
Здесь фаза 0 определяется соотношением: 6= в3 — в2 — ву Отыскивая, как и прежде, инварианты, мы легко находим:
Иг(гУ + щ(гУ = и,
|
(12.В.10) |
Это является отражением закона сохранения энергии. Одновременно с этим получаем:
|
И |
![]() (12.В.11)
(12.В.11)
Последнее соотношение отражает сохранение фазы.
Теперь мы уже в состоянии приступить к обсуждению вопроса, который оставили в стороне в главе 12. А именно: если на входе нелинейного кристалла имеются три волны сог со2 и со3, то каким образом система решает, какую из следующих последовательностей следует реализовать: о)х + а)2 -» со3, со3 — о)х -» со2 или со3 — со2 —> со^. Ответ на этот вопрос дается относительными фазами различных волн. Говоря более точно, в этом случае будет проводиться отбор различных механизмов (генерация суммарной, разностной частот, параметрическое усиление) в соответствии с граничными условиями, определяемыми различными законами сохранения (12.В. 10) и (12.В. И).
Возьмем в качестве примера генерацию суммарной частоты (ЗРв), для которой два граничные условия имеют вид:
М,(0)= м,0 = м|3, и2(0)= м20 = и2}, и3(0)=0 и т. о. со50(г)=О (12.В.12)
В этом случае дифференциальное уравнение относительно и3 имеет вид:
С!£Л
|
(12.В.13) |
![]() <И =
<И =
|
Ти] |
Здесь: I — нормированное расстояние Z = ^ — длина преобразования для
Волны о)ху из есть нормированная амплитуда £/3 =м3/м20, а т есть соотношение первоначальных амплитуд т = (и20/и{0)2. Решение дифференциального уравнения (12.В. 13) может быть выражено с использованием (малоизвестной!) функции численного анализа, а именно — эллиптической функции Якоби, $я(£) (смотрите также дополнение 12.Е). В связи с тем, что математическая природа и значение этой функции не входит в круг вопросов, рассматриваемых в настоящей книге, для наших целей будет достаточно только отметить, что она протабулирована и приводится в современных электронных справочных изданиях. В этом случае интеграл (12.В. 13) дается формулой:
|
(12.В.14) |
![]() С!*
С!*
|
Тх |
![]() Л/1 - X2 л/Г
Л/1 - X2 л/Г
Или:
|
(12.В.15) |
![]() «з(0 = «20 5П
«з(0 = «20 5П
В этом случае решения, дающие амплитуды трех волн, имеют вид:
= «.о — «зо^п|
|
«2 (г У = «20 - «З^У = «20‘ |
|
(12.В.16) |
|
2 10 ..2 > 20 I *ю, |
|
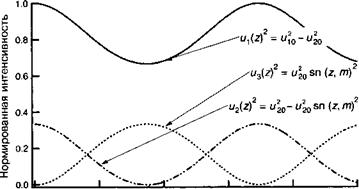
Рисунок 12.В.2 иллюстрирует эволюцию нормированнной интенсивности различных волн «/«ю, и2/мю и из/ию в предположении, что соотношение интенсивностей т= 1/3. Мы видим, что функция Якоби зп(г) является периодической. Физическая природа такой модуляции заключена в периодическом обмене энергией между волнами накачки и 8Рв. Как только волна суммарной частоты соъ полностью истощит волну накачки с частотой а)2, начнется обратный процесс, и волна соъ вновь начнет усиливаться за счет волны суммарной частоты. |
 |
|
|
|
|
|
|
|
|
|
Представленный формализм точно описывает механизм энергетического обмена между различными волнами и выявляет роль, которую играют относительные фазы. Рисунок 12.В.2 показывает, каким образом энергия волн накачки и со2 комбинируется с тем, чтобы сформировать волну суммарной частоты со3 вплоть до полного истощения неосновной волны а)2 когда начинается обратный процесс реконструкции волны а)2 за счет волн сох и соъ и т. д.