Оптоэлектроника

Резонатор Фабри—Перо

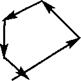
Сейчас мы применим этот формализм к простой задаче, связанной с резонатором Фабри—Перо (смотрите рис. 9.Г. З). Он состоит из диэлектрической пленки толщи­ной 1сау9 покрытой двумя тонкими металлическими слоями. Говоря более точно, эта система содержит пять сред (вакуум —» металл —» диэлектрик -> металл —» вакуум). Полностью эта задача может быть решена при введении комплексного показателя преломления для металла и предположении, что его действительная часть стремит­ся к —оо. Решение этой задачи оставляется читателю. Мы же рассмотрим систему, состоящую из трех сред (вакуум = 1 —» диэлектрик = 2 —» вакуум = 3, при этом металлические слои учитываются с использованием матриц переноса РХ2 и Р2Х, оп­ределяемых соотношениями:

А)е" 1

(9.Г.13)

Р - —

Одним из многих свойств металлических пленок, которое читатель может выве­сти сам в качестве упражнения, является то, что в противоположность диэлектрикам, коэффициенты г12 и т2Х равны. Член е^ отражает вклад дефазировки, обусловленной металлическим зеркалом (0 = я в случае совершенного зеркала), а коэффициент отражения р0 близок к единице и учитывает большое отражение зеркал. Матрица распространения 5^ = РХ202Р23 может быть легко рассчитана из соотношения:

Е"* + р02е'* Л)!?"**"'0 + е|("'9)

+ е1* +р„2е-'*

Это соотношение приводит к пропусканию Грр резонатора Фабри—Перо (смотри­те (9.Г.12):

(9.Г.15)

Таким образом, мы вводим полный коэффициент дефазировки 8 = 2(ф— 0), пропус­кание (Т = |г12|2) и отражение (Я = р02) зеркала. Таким образом, полное пропускание зеркала, т. е. доля интенсивности излучения, падающего слева, которое пересекает резонатор, составляет:

Т2

1 + Я2 -2Ясоьд

Мы напоминаем, что фаза £определяется формулой:

8 = 2

А,

В том случае, когда длина волны излучения, падающего на резонатор, изменя­ется, пропускание осциллирует между минимальным 7п и максимальным Гтах зна­чениями, определяемыми:

Т2

(1 + л)2

Сау

ШАЛЛДА^

Я

Металлические

Зеркала

Рис. 9.Г. З. Резонатор Фабри—Перо.

Тах / ч

(1 - /?)

Если бы зеркала были абсолютно совершенными (Я + Т + А = 1 с коэффици­ентом поглощения зеркала А = 0) мы бы получили Гтах = 1, т. е. вся энергия прошла бы через резонатор. Это могло бы показаться удивительным, как если бы мы сдвигали два зеркала со слабым пропусканием Т, и полное пропускание комби­нированной системы (при определенном зазоре) оказалось бы равным 1 вместо Т2, что мы могли бы ожидать! Этот эффект является результатом конструктивной ин­терференции, что является типичным для волновых явлений. Аналогичный эффект проявляется в случае резонансного туннелирования электронов через двойные кван­товые барьеры.

Подставляя (9.Г. 18) в выражение для пропускания резонатора (9.Г. 16), мы по­лучаем:

Г" ■ г - Т7с5^Т2) (9тл9)

Где С — контраст резонатора, определяемый формулой:

АЯ

Тпт (1 - Я)2

Вблизи резонанса резонатора (<? « 2тт; где т — целое число) (9. Г. 19) принимает вид лоренциана:

1	1
К - в

(9.Г.21)

Пропускание резонатора Фабри—Перо

Здесь А V частотный интервал между оптическими модами, а Р есть зеркальность резонатора, определяемая формулой:

4я

1-Я

Зеркальность резонатора

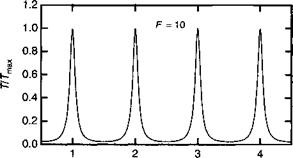
Зеркальность по порядку величины составляет п/Т для Я ~ 1. Рисунок 9.Г.4 пред­ставляет зависимость Т¥? от частоты излучения. Спектральная зависимость пропуска­ния резонатора проявляет ряд максимумов, разделенных частотными интервалами:

С

Эта величина представляет собой межмодовый интервал резонатора (или свободный спектральный диапазон) с полушириной:

Ду

~Т

Именно благодаря этому параметру Р можно интерпретировать как меру зер­кальности.

В случае идеального зеркала (0 = я) резонансы имеют место при толщине резонатора:

С = т -

2 Пп,

Здесь т есть целое число. Таким образом резонансный резонатор Фабри—Перо есть устройство полуволнового типа. Интерпретация резонанса Фабри—Перо при­ведена на рис. 9. Г. 5. На этой диаграмме амплитуды и относительные фазы различ­ных распространяющихся полей представляются векторами Френеля или фазора - ми. В условиях вне резонанса векторы, соответствующие отраженным волнам, скла­дываются (круговым образом), при этом их сумма равна нулю. Все происходит таким образом, как если бы два металлических зеркала вели себя независимо друг от друга и обладали бы пропусканием Т при полном пропускании пары зеркал Т2.

А б в

Рис. 9.Г.5. Когда резонатор Фабри—Перо находится вне резонанса сложение векторов Френеля происходит по круговой траектории (а). При приближении к резо­нансу фазовый сдвиг между каждым вектором становится кратным 2я, при этом отдельные векторы Френеля выстраиваются, что приводит к пропус­канию, близкому к единице (б). Это последнее условие реализуется в полу­волновом резонаторе.

С другой стороны, по мере того как толщина диэлектрического слоя приближа­ется к полуволновому значению, разность фаз между отдельными фазорами стано­вится кратным 2ж (т. е. они начинают выстраиваться вдоль одного направления), при этом они суммируются (интерферируют) конструктивно.

Рассчитаем теперь комплексную амплитуду электрического поля внутри резона­тора, считая зеркала идеальными. Это можно сделать используя [Е2] = Р23[Е3, а так­же (9.Г.1), т. е.:

(9.Г.26а)

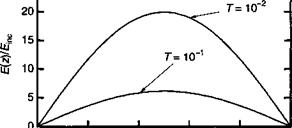
Амплитуда поля внутри резонатора есть модуль (9.Г.26я) (это не является три­виальным результатом и мы оставляем это доказательство читателю в качестве уп­ражнения). Рисунок 9.Г.6 показывает распределение электрического поля в резона­торе. Отметим проявление эффекта резонанса, приводящего к увеличению макси­мальной напряженности поля внутри резонатора. Мы можем легко найти максимальную напряженность поля, предполагая, что в резонансе (т. е. при ф = л и р0 *1) электрическое поле (9.Г.26я) приближается к стоячей синусоидальной вол­не, спадающей до нуля у зеркал при і = 0 и і = /сау при к = я/1слу. Максимальная напряженность поля имеет место при і = /сау /2 или:

(9.Г.266)

Или с учетом (9.Г.5) и (9.Г.21):

(9.Г.26*)

Таким образом интенсивность излучения посередине резонатора усиливается в 4/Г раз по сравнению с входящим потоком, при этом коэффициент 1 /Т обусловлен коэффициентом отражения зеркала, а коэффициент 4 возникает вследствие конст­руктивной интерференции двух волн, распространяющихся в противоположных на­правлениях. Энергия, запасенная в резонаторе, получается интегрированием сину­соидального распределения, т. е.:

(9.Г.27)

Здесь £ есть площадь резонатора. Эту величину следует сравнить с энергией, теря­емой за цикл, что соответствует интегральному фотонному потоку за цикл. Отно­шение этих двух величин, коэффициент качества резонатора б, определяемый (9.Г.27) и (9.Г.23), может быть записано в виде:

25

„ запасенная энергия у 0 г

* ~ .2.0)

Расход энергии за один цикл Ду

Коэффициент качества и зеркальность резонатора для волны с частотой V

Эта величина связана с фотонным временем жизни соотношением:

О = 2 кухс (9.Г.29)

Это соотношение устанавливает связь между г и Р.

Пример----------------------------------------------------------------------------------------------------------

1. Рассмотрим резонатор Фабри—Перо, содержащий диэлектрический стержень дли­ной 50 см с коэффициентом преломления 1,5. Металлические зеркала, наносимые на оба конца стержня, обладают коэффициентом отражения Я = 99% и пропускани­ем Т= 1 — Я = 10“3. В этом случае зеркальность резонатора есть Р = ттЯ/Т = 3140. Межмодовый интервал есть 3 х 108 м с_1/(3 х 0,5 м) или 2 х 108 Гц. Для длины волны

1 Мкм (у = 3 х 1014 Гц) коэффициент качества 0 = 3,14 х 103 х 3 х 1014 Гц/2 х 108 Гц или = 5 х 109! В действительности такой величины трудно добиться, так как трудно обеспечить необходимую степень параллельности зеркал при достаточно большом расстоянии между ними.

2. Теперь рассмотрим резонатор, реализованный с использованием слоя АЮаА$ толщиной 0,25 мкм и п = 3. Длина резонансной волны в резонаторе в этом случае составляет Л0 = 2яор/сау или 1,5 мкм. На обе стороны слоя АЮаА$ наносятся металличес­кие зеркала, обладающие коэффициентом отражения Я = 99,9% и пропусканием Т= 1 — Я = 10 3. В этом случае зеркальность резонатора рассчитывается аналогично предыдущему примеру, Р = пЯ/Т = 3140. В то время как в рассматриваемом случае межмодовый интервал составляет 3 х 108 м с~'/(2 х 3 х 0,25 х 10~6 м) или 1,5 1014 Гц. В этом случае коэффициент качества есть 3,14 х 103х2х 1014 Гц/1,5х 1014 Гц или 0 = 4200.