Механика гидро - и пневмоприводов

Влияние основных нелинейностей на устойчивость гидро — и пневмоприводов

Гидропривод с дроссельным регулированием

Линейные математические модели гидро - и пневмоприво­дов позволяют достаточно просто и эффективно решать не только задачи устойчивости, но и ряд проблем управления ро­ботами, самолетами, энергетическими установками и другими объектами. Однако чтобы получить такие модели, приходится часть нелинейных функций произвольно заменять линейными.

К основным функциям, не линеаризуемым методом малых отклонений, относятся те, которые описывают закономерности истечения рабочих сред через дроссельные устройства и си­лы сухого или смешанного трения, действующие на элементы гидро - и пневмоприводов. Для исследования влияния нелиней­ности этих функций на устойчивость приводов сравним приток энергии в следящий гидропривод с дроссельным регулирова­нием (см. рис. 5.7) и потери (диссипацию) механической энер­гии вследствие действия сил трения при колебаниях выходного звена. Колебания будем считать близкими к гармоническим, что допустимо, когда сила Рс. тр(0) сухого трения в нагрузке на выходное звено по отношению к амплитуде ар первой гармо­ники силы давления на поршень гидроцилиндра удовлетворяет неравенству

Ар > 2,5Рс. тр(0).

Силу Рс. тр сухого трения в этом случае определяет функ­ция

Рс. тр = Рс. тр(О) 816п(?;шх), (6.21)

Где г;шх — скорость штока (выходного звена) гидроцилиндра.

Примем, что шток жестко соединен с телом массой га и на него не действует позиционная нагрузка (сн = 0). При указан­ных допущениях колебания штока можно приближенно опи­сать соотношением

Ушт = Яу Бш(и>о ц^), (6.22)

Где ушт — перемещение штока (выходного звена) гидроцилин­дра; ау и щ ц — амплитуда и частота колебаний штока гидро­цилиндра, причем последняя величина в предположении мало­го демпфирования поршня равна собственной частоте колеба­ний тела массой га.

Работу силы сухого трения за период Го = 27г/о;оц коле­бания штока найдем в виде

То/4

Ас. тр — 4 / - Рс. тр (0)0^0 ц соб^о Ц*) Л = 4ауРс. Тр(0). (6.23) о

Если вместо сухого действует вязкое трение, то работа сил вязкого трения также за период колебания штока составит

То

Лв. тр = ! кТ9ш1па2усоъ2{ио^)& = жкт? шопа2у, (6.24) О

Где А;тр — коэффициент вязкого трения в соотношении, опре­деляющем силу вязкого трения

-^в. тр = ^тр ^ — &тр^0 СОБ^и^о ц^)* (6.25)

Приравняв Ас. хр и Ав. тр из формул (6.23) и (6.24), полу­чим коэффициент гармонически линеаризованного сухого тре­ния

_ 4Рс. тр(0) к хр — •

7Ги>0 ц&у

Соотношение (6.26) позволяет вместо нелинейной функ­ции (6.21) записать

?с. тР = ктр^. (6.27)

Здесь Р с. тр — приближенное значение силы сухого трения, вы­раженной аналогично силе вязкого трения, но отличающейся тем, что коэффициент к тр зависит от амплитуды ау и частоты И)ц-

В случае следящего гидромеханического привода с дрос­сельным регулированием при наличии в нем автоколебаний примем Лвх = 0 (см. рис. 5.7, а, точка А неподвижная). Со­гласно уравнению (5.75),

#з ^о. сУшт - (6.28)

За полупериод, при котором ушт > 0, через окна, откры­тые кромками золотника, протекает расход, который найдем по формуле (5.18) с учетом соотношений (6.22) и (6.28):

Зз = - к'3К0.сау 8ш(ы0цОУ^ ~ ?2 + Рн (б-29)

В отсутствие позиционной нагрузки на выходное звено (Рн = 0) при х3о = 0 по формуле (5.19) получаем

V и /Рп — Рсл

КЯх = *3у------------------------ 2-------

С помощью этой формулы представим функцию (6.29) в

<2з = - КдхК0.сау віп(«оц<)і/і+ ——— (6.30)

V Рп Рсл

Работа, которую может совершить жидкость за период колебания поршня гидроцилиндра, равна

То/2

= 2 ! <2зРн Л. (6.31)

О

После подстановки под интеграл (6.31) функции (6.30)

Имеем

То/2

Ап = 2 I - КдхК0'СауръЬ1п(иоцЬ)* I Н------------------- Л. (6.32)

3 V Рп - Рсл

0

Значения рн зависят от действующей на выходное звено нагрузки. С учетом принятого выше допущения о том, что основной нагрузкой является инерционная, найдем

* = (633)

При законе (6.22) движения поршня гидроцилиндра соот­ношение (6.33) будет иметь вид

Тауи% тт

Рн =------- £---- 8т(ы0цО - (6.34)

Подставив рн из формулы (6.34) в интегральное выраже­ние (6.32), приведем его к виду

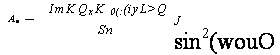
Тауш0 ц sin(u>0 Ц^)

■^(Рп-Рсл)

С помощью соотношений (5.27), <^оц = 1 /7ц, DT = {KQxK0'C)l5„ получим

2mKQxK0.ca2yulli 2

— 2ита, уСц, (6.36)

*~>п

Тауш Оц________ аусп

^(Рп “ Рсл) ^(Рп “ Рсл) где

2/с = SniPn ~ Рсл) (6.38)

Сц

— перемещение штока гидроцилиндра вследствие сжимаемо­сти жидкости под действием силы полного торможения.

Введя переменную ф = UQnt и используя соотношения (6.36)-(6.38), интеграл (6.35) приведем к виду

_ о 7Г

2DTa,.cn [ 0 I ей.

Ап =-------- -— / sin ф* 1------ - sin ф <1ф. (6.39)

И) ц У V Ус

О

Принимая в линеаризованном уравнении (5.17) расходно- перепадной характеристики золотникового устройства Kqp = = 0, получим соотношение, описывающее изменение расхода Q з при малых отклонениях золотника от среднего положения без учета разности давлений в полостях гидроцилиндра:

Зз = KQxx з. (6.40)

Работу Апо, которую может совершить жидкость в гидро­цилиндре при расходе, соответсвующем соотношению (6.40), будет определять формула (6.32), если под корнем пренебречь

Малой по сравнению с единицей величиной рн/(рп — Рсл)• Вы­полняя затем такие же действия, как при выводе формулы (6.39), получаем

К DTa, yCn

Ап о —

И)ц

Отношение

7Г

= — / sin2 фх /l — — Sin7<1ф> (6.42)

AnO * J V 2/с

О

Показывает, насколько работа, совершаемая жидкостью за пе­риод колебания поршня гидроцилиндра при нелинейной рас - ходно-перепадной характеристике золотникового устройства, отличается от работы Апо, вычисленной при использовании приближенной характеристики (6.40).

Обозначив а = ау/ус, (3 — Аи/Апо, можно представить соотношение (6.42) в виде

7Г

(3 = — J sin2 ^л/l — a sin ф <1ф. (6.43)

О

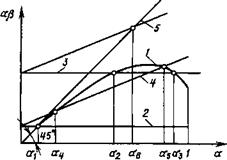
М. Гийон в книге “Исследование и расчет гидравлических систем” (Пер. с фр. М.: Машиностроение, 1964) приме­нил для анализа взаимного влияния нелинейности расходно - перепадной характеристики золотникового устройства и тре­ния в нагрузке на выходное звено гидропривода графики, по­строенные в координатах аОа(3. В таких координатах зависи­мость безразмерной работы, совершаемой жидкостью, от от­носительной амплитуды колебаний определяет функция а/З = = а(а). График этой функции (см. рис. 6.5 кривая 1) ограни­чен значением а = 1 в связи с тем, что при а > 1 под кор­нем в функции (6.43) можно получить отрицательную величи­ну. Это указывает на изменение направления течения жидко­сти через окна, открытые кромками золотника, и возможность возникновения кавитации. При кавитации применявшиеся для определения функции (6.43) соотношения не выполняются.

На рис. 6.5 показаны прямые 2 и 3, соответствующие вы­числяемой по формуле (6.23) работе сил сухого трения, отне­сенной к работе Аио, вычисленной по формуле (6.41). Точки пересечения кривой 1 с прямыми 2 и 3 определяют значения безразмерных амплитуд а<1 и аз колебаний штока гидро­цилиндра, при которых работа, совершаемая жидкостью, бу­дет равна работе сил сухого трения. Колебания с амплиту­дами а и а2 при малейшем их изменении могут быть либо затухающими, либо расходящимися, поскольку слева от этих точек работа сил сухого трения превышает работу, соверша­емую жидкостью, а справа работа жидкости больше работы сил сухого трения.

При колебаниях с амплитудой аз слева и справа от точки пересечения кривой 1 и прямой 3 соотношения между работой жидкости и сил сухого трения таковы, что при этой амплитуде колебания устойчивы, т. е. являются автоколебаниями. Если к работе сил сухого трения добавить относительную работу сил вязкого трения, вычисляемую по формулам (6.24) и (6.41), то на рис. 6.5 будем иметь прямую 4. Кривая 1 пересекает прямую 4 также в двух точках. Автоколебания теперь могут быть с амплитудой а5.

Без учета нелинейности расходно-перепадной характери­стики золотникового устройства и при расчете расхода по со­отношению (6.40) получим на рис. 6.5 прямую 5. До значе­ния а 0,1 кривая 1 и прямая 5 практически совпадают, что указывает на малое отличие математической модели ги­дропривода с линеаризованной характеристикой дроссельного устройства и гидропривода с близкой к реальной нелинейной расходно-перепадной характеристикой золотникового устрой­ства. По соотношению работ сил трения и жидкости в окрест­ности точек пересечения прямых 2, 3 и 4 с прямой 5 можно заключить, что сами по себе силы сухого трения в нагрузке не могут быть причиной возникновения в гидроприводе авто­колебаний.

В случае линеаризованной расходно-перепадной характе­ристики золотникового устройства и вязкого трения в нагрузке математическая модель гидропривода позволяет только выяс­нить, устойчив ли гидропривод (график работы сил вязкого трения расположен выше прямой 5) или неустойчив (график работы сил вязкого трения расположен ниже прямой 5).

Заметим, что рассмотренный выше анализ энергетическо­го баланса при наличии в гидроприводе колебаний является приближенным, так как основан на предположении о значи­тельном превышении инерционной нагрузки над другими ви­дами нагрузки, действующими на выходное звено привода. В противном случае закон изменения разности ри давлений в по­лостях гидроцилиндра может существенно отличаться от вы­ражения (6.34), что вызовет изменение зависимости Аи от ам­плитуды колебаний штока гидроцилиндра. Кроме того, при значительных силах сухого трения колебания поршня гидро­цилиндра не будут близкими к гармоническим и могут даже носить характер периодических движений, описываемых раз­рывными функциями.

Следящий пневмопривод

Пневмоприводы в отличие от гидроприводов имеют рас- ходно-перепадные характеристики, которые в более широком диапазоне значений ри можно считать линейными. При при­нятых выше допущениях о преобладающей роли инерционной нагрузки в формировании закона движения выходного звена влияние сил сухого и вязкого трения на устойчивость пнев­мопривода можно оценить с помощью графиков, аналогичных представленным на рис. 6.5.

Прямая 5 в данном случае будет графиком безразмер­ной работы, совершаемой газом в полостях пневмоцилиндра при критическом течении газа через золотниковое устройство. График ограничен справа значениями а, при которых течение газа через золотниковое устройство станет докритическим.

В докритическом режиме течения расход газа изменяется с изменением ря и вследствие этого совершаемая газом работа будет уменьшаться приблизительно так же, как и в гидропри­воде (см. рис. 6.5, кривая ]). Граничные значения агр имеют место при

Ря /-

> (Рн)кр>

Рп ~~ Рсл

Где (рн)кр — безразмерная разность давлений в пневмоцидин - дре, при которой наступает докритическое течение газа через золотниковое устройство.

Подставив в это неравенство значение рн из формулы (6.34), используя формулу (6.38) и соотношение а = ау/ус, получим граничное значение агр, при превышении которого будет докритическое течение газа через золотниковое устрой­ство. Согласно расходно-перепадной характеристике, приве­денной на рис. 3.23, (Рн)кр = 0,65.

Для пневмопривода кривая 1, показывающая, как влияет нелинейная расходно-перепадная характеристика на совершае­мую жидкостью работу, заметно отклоняется от прямой 5 при а « 0,3.