Механика гидро - и пневмоприводов
Устойчивость гидро — и пневмоприводов при малых отклонениях фазовых координат и во всем фазовом пространстве
Гидро - и пневмоприводы могут быть достаточно сложными динамическими системами. Пригодность таких систем для практического использования, прежде всего, зависит от того, удовлетворяют ли они условиям устойчивости в смысле фундаментальных понятий, принятых в механике и теории управления. Рассмотрим основные вопросы устойчивости, обратившись к математическим моделям (см. § 4.1) систем в переменных состояния.
При реальном процессе В системе переменные XI у Х2, Яз, хп будут функциями времени, которые являются решениями уравнения (4.1) при заданных начальных условиях и заданном изменении со временем вектора и. В пространстве, координатами которого служат переменные состояния, эти решения определяют положение изображающей точки. С течением времени изображающая точка перемещается по траектории, которую называют фазовой, а пространство, в число координат которого явно не входит время £ и компоненты вектора и, называют фазовым пространством. Если переменные хч х2> 1 хп выбраны в виде отклонений от значений х^о,
£2.о > х3.о> 5 хп.0) полученных при равновесном состоянии си
Стемы, то начало координат фазового пространства можно совместить с точкой, соответствующей их установившимся значениям.
Способность системы, будучи отклоненной от равновесного состояния, возвращаться к нему с заданной точностью, характеризует систему как устойчивую. В тех случаях, когда в фазовом пространстве существует только одна точка равновесия и система устойчива при любых изменениях переменных, она будет устойчива во всем фазовом пространстве. Таким свойством обладают только системы, процессы в которых можно описать линейными дифференциальными уравнениями без каких-либо ограничений на значения переменных состояния и вид возмущающих или управляющих воздействий. Однако для реальных систем данное условие не выполняется, так как их линейные математические модели получают только в результате аппроксимации нелинейных функций путем перехода к малым отклонениям переменных (см. § 4.2). Следовательно, по таким линеаризованным моделям устойчивость системы проверяется только при малых отклонениях фазовых координат. Определение практически допустимых отклонений переменных, при которых результаты исследования устойчивости системы по ее линеаризованной модели будут справедливы, требуют дополнительных расчетов или физических экспериментов. Вследствие нелинейности характеристик отдельных элементов систем и нелинейности функций, описывающих взаимодействие элементов в системе, в фазовом пространстве может быть несколько особых точек. При этом в окрестности одних точек система устойчива, а в окрестности других
— неустойчива. Вблизи последних точек фазовые траектории могут быть замкнутыми кривыми, указывающими на существование в системе предельных циклов (автоколебаний).
Наиболее общую постановку задачи устойчивости систем предложил в 1892 г. А. М. Ляпунов, выделив невозмущенное и возмущенное состояния системы, которую описывают дифференциальными уравнениями
У2, • ,Уп,0> к = 1,2, . ,п. (6.1)
Где у к — координаты, определяющие состояние системы;
У2> , Уп, *) — нелинейные функции.
При известных для невозмущенного состояния системы функциях времени
У10 = Ую(0> У20 = У2о(0. УпО = Упо(<) можно ввести новые переменные
Хк = Ук - Ук о(0-
В новых переменных уравнения (6.1) принимают вид
Где
, *п, <) = ^(УЬ »2, , Уп, 0-
-У*(У10> У2 О, , Уп0><)-
Дифференциальные уравнения (6.2) описывают возмущенное состояние системы. Отклонения Хк(Ц) координат в начальный момент времени являются возмущениями.
Каждое возмущенное состояние системы определяет свое решение уравнения (6.2). Невозмущенному состоянию соответствует решение
Х1 = х2 = = Хп = 0.
При равновесии (установившемся движении) стационарной (параметры не зависят от времени) системы
^ь(ую, 2/2 0) УУп о) = 0.
Невозмущенное состояние системы устойчиво, если для любого положительного сколь угодно малого числа е можно выбрать такое положительное число //(б), при котором для всех возмущений я*(<о)> удовлетворяющих условию
Хк(*о) ^ *?(е)> будут выполняться неравенства
Если
|
|
То имеет место асимптотическая устойчивость.
|
(6.3) |
![]() При условии, что правые части уравнения (6.2) могут быть линеаризованы разложением в ряд Тейлора (см. § 4.2), эти уравнения заменяют уравнениями первого приближения
При условии, что правые части уравнения (6.2) могут быть линеаризованы разложением в ряд Тейлора (см. § 4.2), эти уравнения заменяют уравнениями первого приближения
|
|
= ак 1Х1 + ак 2Х2 + + Чпхп,
Где а^2? ->акп — коэффициенты, получаемые при линеаризации фуНКЦИЙ Х*.(Х1, Х2> > хп, О*
В соответствии с теоремами, сформулированными и доказанными Ляпуновым, невозмущенное состояние системы асимптотически устойчиво, если вещественные части всех корней характеристического уравнения, полученного для уравнений
(6.3) первого приближения, отрицательны. Если среди корней будет хотя бы один с положительной вещественной частью, то система неустойчива, а при нулевом корне об устойчивости системы нельзя судить по уравнению первого приближения. Важно отметить, что указанные условия не зависят от того, какие члены высших порядков были отсечены при линеаризации функций в правых частях уравнения (6.2). Когда эти функции нельзя линеаризовать разложением в ряд Тейлора (методом малых отклонений), для проверки устойчивости применяют метод, который, наряду с другими методами исследования нелинейных систем, изложен в теории управления (второй метод Ляпунова).
Условие асимптотической устойчивости следует также непосредственно из решения линейного дифференциального уравнения, которое можно найти, сложив частное решение неоднородного уравнения и общее решение однородного уравнения (с правой частью, равной нулю). Первое решение определяет вынужденную составляющую рассматриваемого процесса (невозмущенное состояние системы), второе — описывает переходную составляющую процесса (возмущенное состояние системы). Эту составляющую находят в виде суммы
|
П
К=1 |
Где Сь — постоянные величины, А*. — корни характеристического уравнения. В случае только отрицательных вещественных частей А*, при / —► оо переходная составляющая стремится к нулю и система приближается к невозмущенному состоянию. Такая связь между устойчивостью технических систем и значениями корней характеристических уравнений была замечена даже несколько раньше появления общей теории Ляпунова. В 1875 г. Э. Раус предложил алгебраический критерий, позволяющий без решения характеристического уравнения проверить, все ли корни имеют отрицательные вещественные части, т. е. расположены на комплексной плоскости слева от мнимой оси. Затем в 1895 г. А. Гурвиц разработал критерий, получивший широкое применение в приложениях. Согласно этому критерию, для устойчивости системы необходимо и достаточно, чтобы все коэффициенты характеристического уравнения и определители Дп, Дп_1, , Д1 были положительными. Опреде
Лители составляются из коэффициентов характеристического уравнения
ЯпАп + ап—хА71 * + ... аА + ао = О,
(6.4)
Начиная с определителя
|
О Йп Ап—2 |
|
О Ап—1 <*п-3 |
|
Ап-1 Ап—3 ап—5 |
|
Ап Ап-2 Ап—4 |
|
Дп = |
 |
|
|
|
||
0 0 0 0 а0
Все последующие определители Дп_1, Дп-2) являются минорами элементов определителя Дп, которые получают вычеркиванием столбцов и строк, начиная с правого столбца и нижней строки.
Таким образом, критерий Гурвица можно записать в виде следующих неравенств:
|
(6.6) |
![]() Ао >0, а > 0, ап > 0;
Ао >0, а > 0, ап > 0;
Д1 >0; Д2 > 0; Дп > 0.
Для характеристического уравнения п-й степени Дп = = аоДп-ь а так как в соответствии с (6.6) ао должно быть положительной величиной определители вычисляют, начиная
с определителя Дп_1. При п = 3 система устойчива, если все коэффициенты больше нуля и определитель Д2 > 0, поэтому условие устойчивости сводится к неравенству
А(12 > аоаз - (6-7)
Условие (6.7) показывает, что система, математическая модель которой представлена линейным дифференциальным уравнением третьего порядка, будет устойчива, если все коэффициенты уравнения имеют одинаковые знаки (положительные) и произведение коэффициентов при средних членах больше произведения коэффициентов при крайних членах.
Устойчивость следящего гидропривода с дроссельным регулированием
Применим критерий для анализа устойчивости следящего гидромеханического с дроссельным регулированием, структурная схема которого дана на рис. 5.7, б. Передаточную функцию замкнутого контура привода с помощью формулы (4.60) представим в виде
Ф,1 ГштМ и'сМк. к
* />.хМ 1 + «,,(1)' ' 1
Из передаточной функции (6.8) следует, что
[1 + К0.с1Гс. ч(з)] Ушт(з) = №с. ч(з)Кхк?1вх(з). (6.9)
Однородному дифференциальному уравнению соответствует левая часть уравнения (6.9), поэтому характеристическое уравнение можно найти, приравняв нулю знаменатель передаточной функции (6.8)
Передаточную функцию И/С. ч(^) определим, используя структурную схему на рис. 5.3, а и формулу (4.60)
И/с’ч(5) = Тгз(Ту + 2(иТцз + 1) + Кн' (6-П)
После подстановки И^.ч^) из формулы (6.11) в уравнение (6.10) получим
ТгТцЗ^ + 2£цТ’гТ'цЗ^ + Тгз + Ки + К0Л = 0. (6.12)
Уравнение (6.12) является характеристическим уравнением исследуемого следящего гидромеханического привода. Все коэффициенты уравнения положительные числа, поэтому, согласно (6.7), привод устойчив, если
2СцТг > (*н “Ь К0.с)Тп. (6.13)
У большинства реальных гидроприводов значение Кк мало по сравнению с K0tC. Пренебрегая Кк и применяя формулы (5.26-5.30), условие устойчивости (6.13) представим в параметрах привода:
(krр + > mDT. (6.14)
В это неравенство входит важная для оценки динамических свойств гидропривода величина, называемая добротно - стью гидропривода
Которая характеризует его быстродействие.
Из неравенства (6.14) следует, что устойчивость гидропривода в значительной мере зависит от значений коэффициентов А;тр и Kqp. Если в нагрузке на выходное звено отсутствует трение (А;тр = 0), то гидропривод может быть устойчив только при Kqp >0. В то же время формула (5.20) показывает, что с приближением к равновесному состоянию (х3 —► 0) значение Kqp —> 0, если в золотнике нет утечек и перетечек жидкости по зазорам (идеальный золотник). Кроме того, условие (6.14) ограничивает значение добротности DT гидропривода и тем самым ограничивает его быстродействие.
Аналогичный анализ устойчивости не трудно выполнить как в случае следящего пневмомеханического привода, так и для гидропривода с объемным регулированием. Для этого можно использовать структурные схемы, показанные на рис. 5.3, б и рис. 5.5. Если математическая модель электроги - дравлического или электропневматического усилителя имеет вид, близкий к модели ЭГУ с механической обратной связью, структурная схема которого дана на рис. 5.10, то анализ устойчивости ЭГУ также не будет сложнее рассмотренного.
Частотные методы проверки устойчивости управляемых систем
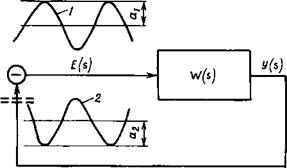
При наличии в структурной схеме нескольких динамических звеньев возрастает степень характеристического уравнения, что может усложнить получение обозримых данных о влиянии вида и параметров звеньев на устойчивость системы с помощью критерия Гурвица. В таких случаях целесообразнее применить частотный критерий, который предложил в 1932 г. Г,»Найквист. Физический смысл критерия состоит в следующем. Когда линейная система с отрицательной обратной связью находится на границе устойчивости, в ней чаще всего возникают колебания, которые будут незатухающими, пока гармонический сигнал 1 (рис. 6.1) после узла суммирования равен по амплитуде сигналу перед узлом суммирования и смещен от него по фазе на -180° Это смещение по фазе обусловлено тем, что обратная связь является отрицательной (в узле знак “минус”). Отставание по фазе сигнала 2 от сигнала 1 могут создать звенья, динамические свойства которых описывает передаточная функция И^з). Таким образом, замкнутая отрицательной обратной связью система будет находиться на границе устойчивости, если при прохождении гармонического сигнала по ее разомкнутому контуру (место размыкания контура показано на рис. 6.1 двумя штриховыми линиями перед узлом суммирования) смещение по фазе составит —180° при отношении амплитуд а^/ах — 1.
|
Рис. 6.1. Изменение амплитуды и фазы гармонического сигнала в замкнутом контуре системы |
Для устойчивости системы (колебания затухают) при смещении по фазе —180° отношение амплитуд а2/ а должно быть меньше единицы.
Математической основой критерия Найквиста служит известный из теории функций комплексного переменного принцип аргумента, согласно которому у многочлена
D(s) = ansn + on_isn_1 + +ois + a0
Все нули будут расположены на комплексной плоскости слева от мнимой оси, если приращения аргумента функции, полученной после подстановки s = ju в многочлен, составит
Д aigD(ju) = 7Г ^ (6.16)
При изменении и от 0 до +00.
Как уже было сказано ранее, для устойчивости системы необходимо, чтобы вещественные части корней ее характеристического уравнения были отрицательными числами, т. е. корни располагались на комплексной плоскости слева от мнимой оси. Характеристическое уравнение можно найти, приравняв нулю знаменатель передаточной функции замкнутой системы. Для замкнутой системы, показанной на рис. 6.1, передаточная функция имеет вид
W(s)
*« = Y
+ W(s)
Знаменатель Ф(з) содержит передаточную функцию разомкнутой системы
( > E(s) Dt(S) ’
Поэтому
В соотношении (6.17) числитель Dp(s) + Mp(s) и знаменатель Dp(s) являются левыми частями характеристических уравнений замкнутой системы и ее разомкнутого контура соответственно. У реальных систем степень полинома Mp(s) равна или меньше степени полинома J9p(«s), которую примем равной 71, поэтому степень полинома Dp(s)+Mp(s) также будет равна 71.
В этом случае замкнутая система с неустойчивым разомкнутым контуром будет устойчива, если приращение аргумента функции 1 + W(ju) при изменении и от 0 до +оо составит
Д arg[l + W(ju)] = ^[п — (п — к) + к] = 7гА:, (6.18)
Где к — число корней характеристического уравнения разомкнутого контура системы, расположенных на комплексной плоскости справа от мнимой оси.
При устойчивом разомкнутом контуре системы к = 0, и формула (6.18) принимает вид
Д arg[l + W(ju) — 0. (6.19)
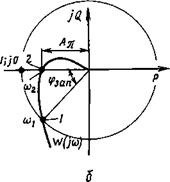
На комплексной плоскости 1 + W(ju) можно представить вектором, начало которого лежит в точке с координатами (-1; j0), а конец обегает АФЧХ W(ju) разомкнутого контура системы (рис. 6.2). В соответствии с этим рисунком и условием (6.19) критерий Найквиста формулируется следующим образом: замкнутая система устойчива, если АФЧХ ее устойчивого разомкнутого контура при изменении и от О до +оо не охватывает точку с координатами ( — 1; j0).
Впоследствии на основе условия (6.18) формулировка критерия была расширена и дана в виде: замкнутая система
Устойчива, если АФЧХ ее неустойчивого разомкнутого контура при изменении и от 0 до +оо проходит на комплексной плоскости так, что приращение аргумента функции l + W(ju>) равно 7Г&, где к — число корней характеристического уравнения разомкнутой системы с положительной вещественной частью.
Характеристическое уравнение разомкнутого контура системы с интегрирующим звеном имеет один нулевой корень. Такие разомкнутые контуры называют нейтрально устойчивыми. Доказано, что для проверки замкнутых систем с нейтрально устойчивыми разомкнутыми контурами также можно применить частотный критерий Найквиста.
|
Рис. 6.2. АФЧХ разомкнутого контура при проверке устойчивости замкнутой обратной связью системы |
Условия, которым должны удовлетворять АФЧХ разомкнутых контуров систем, чтобы замкнутые системы были устойчивы, достаточно просто перенести на логарифмические амплитудные и фазовые частотные характеристики. Для примера обратимся к следящему гидромеханическому приводу с дроссельным регулированием, анализ устойчивости которого был выполнен с помощью критерия Гурвица.
Передаточная функция разомкнутого контура системы в данном случае (см. рис. 5.7, б) имеет вид
№{з) = КМз)=-щ?^-—у (МО)
Из передаточной функции (6.20) следует, что разомкнутый контур состоит из последовательно включенных трех типовых звеньев: пропорционального с коэффициентом усиления, равным К0'С, интегрирующего с постоянной времени Тг и колебательного (при (ц < 1) с постоянной времени Тц (рис. 6.3, а). Характеристическое уравнение разомкнутого контура системы определяет знаменатель передаточной функции (6.20), приравняв который нулю, нетрудно найти корни: один нулевой и два комплексных с отрицательной вещественной частью. Следовательно, разомкнутая система является нейтрально устойчивой.
|
Ко, с |
/ |
/ |
||||
|
Rfs* +2fyrqS+t |
|
|
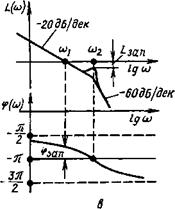
Рис. 6.3. Разомкнутый контур (а), его АФЧХ (б), ЛАХ и ЛФХ (в) при проверке устойчивости следящего привода с помощью критерия Найквиста
Подставив в формулу (6.20) 5 = получим АФЧХ разомкнутого контура системы. Эта характеристика, построенная при К0,с = 1) дана на рис. 6.3, б. Согласно критерию Найквиста, замкнутая система устойчива, так как точка (—1; ^0) не охвачена АФЧХ разомкнутого контура.
С увеличением коэффициента усиления К0,с АФЧХ будет приближаться к точке (—1; ^’0) и при каком-то его значении пройдет через эту точку, а при дальнейшем увеличении К0,с будет ее охватывать. Замкнутая система станет неустойчивой. Возникновение неустойчивости гидромеханического привода при увеличении К0'С соответствует неравенству (6.13), полученному с помощью критерия Гурвица, что вполне закономерно, так как исследование устойчивости выполнено по одинаковым математическим моделям привода.
Построим теперь ЛАХ и ЛФХ разомкнутого контура исследуемой системы, принимая К0,с = 1, Тг > Тп и 0 < Сц < 1-
Поскольку составляющие систему звенья соединены последовательно, просуммируем при одинаковых частотах ординаты ЛАХ и ЛФХ интегрирующего (см. рис. 4.4, в, г) и колебательного (см. рис. 4.9, в, г) звеньев. В результате получим характеристики, изображенные на рис. 6.3, в. Точкам 1 и 2 АФЧХ ¥{1и) на рис. 6.3, б соответствуют точки на ЛАХ и ЛФХ (рис. 6.3, в), для которых частоты равны и и2. Сравнивая эти характеристики нетрудно заметить, что на тех и других можно указать величины, от значения которых зависит, будет ли устойчива замкнутая система. Такими величинами являются А*, </?зап и £зап, причем £зап = 20^(1/А7Г). Величину <^зап называют запасом по фазе, а величину £зап — запасом по амплитуде. Когда АФЧХ проходит через точку ( —1; ^0), значения </?зап и Хзап обращаются в нуль.
Многочисленные расчеты разнообразных линейных систем показали, что при излишне больших запасах по амплитуде и по фазе системы имеют малое быстродействие, вследствие чего увеличивается продолжительность переходных процессов. При очень малых </?зап и Хзап возрастает колебательность переходных процессов.
Наиболее приемлемые по продолжительности, колебательности и максимальным отклонениям переменных переходные процессы обеспечивают запасы по фазе </?зап = 30 ... 40° и запасы по амплитуде Хзап = 6 ... 8 дБ.
Значения запасов по фазе и амплитуде можно изменить в определенных пределах увеличением или уменьшением коэффициента усиления разомкнутого контура системы (в рассмотренном следящем приводе — коэффициентом К о. с)• При увеличении К0'С логарифмическая амплитудная характеристика разомкнутого контура следящего привода смещается вверх на 20 ^ К0.с (что равносильно перемещению на такую же величину оси частот вниз). Логарифмическая фазовая характеристика не изменяется. Вследствие такого смещения частота среза о;Ср, при которой ЛАХ пересекает ось частот, смещается вправо, что вызывает уменьшение Хзап и </?зап - Уменьшение К0'С позволяет увеличить Хзап и </?зап- Логарифмическая амплитудная характеристика показывает также, что на устойчивость системы существенно влияет коэффициент относительного демпфирования, при уменьшении которого уменьшается ^зап-
Если изменить соотношение между постоянными времени так, что значение Тг станет меньше Тц, то частоты и и>2 поменяются местами и замкнутая система будет неустойчивой. Отмеченное влияние всех параметров следящего гидромеханического привода с дроссельным регулированием можно проследить и по неравенству (6.13).
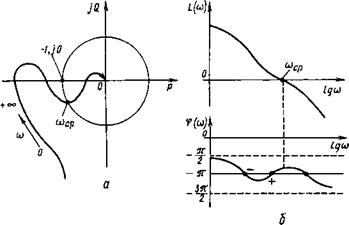
Амплитудно-фазовые частотные характеристики разомкнутых контуров систем с более сложными структурными схемами могут иметь несколько точек пересечения с отрицательной частью действительной оси (рис. 6.4, а). Устойчивость таких систем проверяют по ЛАХ и АФХ (рис. 6.4, 6) разомкнутых контуров, руководствуясь следующим правилом. За - мкнутая система устойчива, если разность положительных и отрицательных переходов фазовой характеристики разомкнутого контура через прямую “—к” равна к/2 в диапазоне частот, при которых Ь[и) > 0. Здесь положительный переход означает пересечение фазовой характеристикой линии (—7г) снизу вверх, а отрицательный — сверху вниз. При неустойчивом разомкнутом контуре системы, для которого к = 1, чтобы выполнялось условие устойчивости замкнутой системы, фазовая характеристика сначала должна находиться между значениями —7Г и —37Г/2, а затем иметь один положительный переход при Ь(и) > 0. Тогда разность числа переходов будет равна 1/2.
Чтобы исследовать устойчивость системы с несколькими замкнутыми контурами (см. рис. 5.12), в первую очередь проверяют устойчивость внутренних контуров, начиная с того контура, который состоит из прямой цепи и обратной связи (см. рис. 5.12, контур 3). Если этот контур устойчив, то его заменяют одним звеном, для которого с помощью формулы (4.60) после подстановки 5 = ]и вычисляют ЛАХ и ЛФХ. С таким звеном проверяют устойчивость следующего внутреннего контура (см. рис. 5.12, контур 2), а затем, как и в предыдущем расчете, находят для него логарифмические частотные характеристики. Затем проверяют устойчивость основного контура (см. рис. 5.12, контур 1), в котором внутренние контуры сведены к одному звену. Если будет обнаружена неустойчивость хотя бы одного внутреннего или основного контура, то
|
Рис. 6.4. Общий вид АФЧХ (а), Л АХ и ЛФХ (б) при проверке устойчивости систем |
Ее необходимо устранить либо изменением его параметров, либо включением корректирующих звеньев.
При корректировании системы следует учитывать, что устойчивость системы с неустойчивым разомкнутым контуром обеспечивается, если выполнено условие приведенного выше в расширенной формулировке критерия Найквиста. Способы корректирования следящих гидро - и пневмоприводов рассмотрены далее в § 6.4.