Механика гидро - и пневмоприводов
Общий вид математических моделей с сосредоточенными и распределенными параметрами
В различных областях человеческой деятельности с давних пор используют моделирование как средство получения информации о поведении тех или иных объектов. При моделировании реальный объект заменяют его физическим или абстрактным прообразом. Если в последнем случае описание происходящих в объекте процессов выполнено в математической форме, то модель называют математической. Благодаря интенсивному развитию вычислительной техники математическое моделирование в настоящее время играет ведущую роль при решении разнообразных научных проблем, при создании и эксплуатации новых сооружений, устройств, систем, а также при управлении производством, решении экономических, социальных и других задач.
Чтобы избежать излишне сложных, а также чрезмерно упрощенных и не адекватных реальным объектам моделей, необходимо не только достаточно глубоко знать сущность моделируемых процессов, но и владеть методами оценок допущений, принимаемых при составлении математических моделей. При математическом моделировании гидро - и пневмоприводов эти общие положения не менее важны, чем при моделировании других, часто более сложных, технических систем.
Как отмечалось в предыдущих главах, математическое описание процессов в гидро - и пневмоприводах основано на фундаментальных уравнениях механики твердого тела, механики жидкости и газа, электротехники и электроники. Если переменные в этих уравнениях не зависят от времени, при системном анализе их называют уравнениями статики, а если зависят от времени — уравнениями динамики. Оба понятия несколько шире, чем принятые в теоретической механике, так как, во-первых, переменными могут быть как механические, так и другие физические величины, и, во-вторых, к равновесным относят такие состояния систем, при которых переменные не изменяются во времени, хотя отдельные части системы находятся в движении. Примерами равновесных состояний, в указанном здесь смысле, могут служить вращение вала двигателя с постоянной угловой скоростью или поступательное движение выходного звена привода с постоянной скоростью. Уравнения статики получают либо непосредственно исходя из условий, определяющих равновесные состояния системы, либо с помощью уравнений динамики, полагая в них равными нулю производные по времени от переменных, описывающих мгновенные состояния системы.
На сложность математических моделей гидро - и пневмоприводов в значительной мере влияет форма описания процессов в рабочих средах и их взаимодействия с элементами приводов. Использование уравнений механики жидкости и газа в гидравлической форме (см. гл. 2 и 3) позволяет упростить математические модели рассматриваемых устройств и привлечь для расчетов экспериментальные значения тех параметров, которые нельзя вычислить. Если в этих моделях допустимо не учитывать изменение гидротермодинамических величин в зависимости от геометрических координат, то описание процессов можно представить в сосредоточенных параметрах. При наличии гидравлических и пневматических линий, протяженность которых превышает 1/4 длины волны колебаний среды вдоль линии, может возникнуть необходимость перехода к более сложным моделям с распределенными параметрами.
Величины, полностью описывающие в данный момент времени состояние какой-либо системы при известных внешних на нее воздействиях, называют переменными состояния.
Такие переменные являются своего рода координатами пространства физических величин, в котором состояние системы, в частности гидро - или пневмопривода, определяет вектор - столбец, имеющий после транспонирования следующий вид:
Х(хь Z2, х3, ..., хп)т,
Где XI, Z2, жз, ., хп — переменные состояния.
В том же пространстве внешние воздействия на систему можно представить после транспонирования в виде
И(«ь«2, т, -,иг)т
Компонентами этого вектора служат управляющие и возмущающие воздействия, приложенные в разных местах системы.
Из числа переменных состояния выделяют наблюдаемые, или, как их еще называют, контролируемые величины
У{У1,У2,УЗ, Ут)Т
В перечисленных переменных основу математической модели гидро - или пневмопривода составляет векторное дифференциальное уравнение состояния
^ = f(x, u, t) (4.1)
И векторное алгебраическое уравнение наблюдаемых переменных
У = g(x, u, t). (4.2)
Правые части уравнений (4.1) и (4.2) в общем случае являются нелинейными функциями векторных переменных X, и и времени <, наличие которого в указанных функциях связано с возможным изменением (нестационарностью) параметров системы, характеризующих ее свойства.
К уравнениям (4.1) и (4.2) необходимо добавить функции, описывающие изменения во времени управляющих и возмущающих воздействий на систему, а также указать началь
Ные условия для системы. Все переменные зависят только от времени, поэтому уравнения вместе с начальными условиями
описывают гидро - или пневмопривод как систему с сосредоточенными параметрами. При наличии в системе физических величин, которые кроме времени зависят еще от геометрических координат, в математическую модель войдут уравнения в частных производных. Такая модель будет соответствовать системе с распределенными параметрами.
Для более подробного изложения процедуры получения математической модели системы с распределенными параметрами предположим, что процессы в гидроприводе необходимо описать с учетом изменения в одном из трубопроводов давления и скорости жидкости не только во времени, но и по длине трубопровода. Кинематическую вязкость жидкости примем постоянной, объемную — равной нулю. Трубопровод будем считать цилиндрическим с круглым проходным сечением диаметром (/о = 2го. При составлении уравнений воспользуемся цилиндрической системой координат, ось х которых направлена по оси трубопровода, а координата г — по радиусу его проходного сечения. В случае неустановившегося осесимметричного течения жидкости уравнения Навье-Стокса (см. гл. 2) при перечисленных условиях можно привести к следующим двум уравнениям:
|
1 дих 1 д _1------- ~ -|--------- Г дг 3 дх |
![]()
|
1 диг ^ г дг |
![]()
|
(4.3) |
![]()
Дих дих дих 1 др
~^Г + их— + ит— = — — + V дt ох от р ох
Дит диг диг 1 др ’4 д2их д2их^
3 дх2 дг2
4 /д2иг 3 дг2
|
(4.4) |
![]() Иг д (1 дих диг
Иг д (1 дих диг
Г2/ дх 3 дг дх)
Дг ' дх
Где их, иг — проекции скорости и на оси цилиндрических координат.
В цилиндрических координатах уравнение неразрывности записывают в виде
Др дит ит дих др др, л
■Ш + '-а7 + >’7 + /’-^ + '‘'/г + и*Тг=0 (4'5)
Уравнения (4.3)-(4.5) можно упростить, если в них пренебречь членами, порядок которых значительно ниже сохраняемых членов. Примем длину I трубопровода линейным масштабом, среднюю по проходному сечению трубопровода скорость у жидкости — масштабом скорости, отношение I к скорости со звука в жидкости — масштабом времени исследуемого процесса. При таких масштабах порядок членов в уравнениях можно определить так:
°Ш = Т <«>
Где символ О, как и в гл. 3, обозначает порядок величины.
|
Д2их 1 ди |
![]() Согласно выражениям (4.6) и (4.7) член их(дих/дх) допустимо считать малым по сравнению с дих! д1, если V С со - Это условие, например, будет выполнено при достаточно распространенных значениях V = 6...7м/си со = 800... 1000м/с. Проведя аналогичные оценки других членов при г < /, представим уравнения (4.3) и (4.5) в усеченном виде:
Согласно выражениям (4.6) и (4.7) член их(дих/дх) допустимо считать малым по сравнению с дих! д1, если V С со - Это условие, например, будет выполнено при достаточно распространенных значениях V = 6...7м/си со = 800... 1000м/с. Проведя аналогичные оценки других членов при г < /, представим уравнения (4.3) и (4.5) в усеченном виде:
|
X |
![]() Дих 1 др
Дих 1 др
= — -5- + V
Дг2 г дг
Р дх
Значения плотности р вследствие ее малого изменения можно принять постоянными при вычислении коэффициентов уравнений (4.8) и (4.9). Уравнение (4.4) при их » иг можно исключить из рассматриваемой системы уравнений.
Для математического описания неустановившегося течения вязкой сжимаемой жидкости в трубопроводе в гидравлической форме умножим все члены уравнений (4.8) и (4.9) на
2жгйг и затем проинтегрируем их в пределах от г = 0 до г = го-
В результате получим
Го го г0 , -
Д [п, 1 д [п , [п {& их 1 дих
Ш Гхп**г = —ра; }2жгр*г+" }2жт-д*+-г-а7)'1т+
О 0 0
+§£/Ч£+тЬ (410)
О
^ 12тггрЛг + р^тг (^ + у) <1г+
Го
+/9— / 2кгих <1г = 0. (4.11) о
Интеграл в левой части уравнения (4.10) равен объемному расходу ф жидкости, протекающей в данный момент времени через рассматриваемое сечение трубопровода
ГО
1 2кгих(1г = (д. (412)
Первый интеграл в правой части того же уравнения равен Го
! 2'кгрйг = 7ГГоР, (4-13)
Так как давление р можно считать независимым от г.
|
/ о (д2их, 1 дих , о дих о |
![]() Второй интеграл в правой части уравнения (4.10) представим следующим образом:
Второй интеграл в правой части уравнения (4.10) представим следующим образом:
27ГГ°Г0н-, (4.14)
Г=г0 Р*
Где нестационарное касательное напряжение на стенке трубо-
Провода определяется соотношением
Дих
|
Dr |
![]()
|
Г=г0 |
![]() Тон = - ри
Тон = - ри
Наконец, вычислим третий интеграл в правой части уравнения (4.10):
J 2жг dr = 2ж J г dr + 2ж J ит dr =
0 0 0
Го го
|
/ |
Du 0 / du
R-^-dr + 2житг — 2ж I гdr = 2жгourQ. (4.16)
0 0 0
Учитывая упругую деформацию стенок трубопровода, имеем
Дго
Ит0 ~ at •
Приращение го связано с приращением Ар давления в трубопроводе соотношением
Г0
Дг = —— (г0Ар + рАг0),
О J^ct
Где Ест — модуль упругости материала стенки; 6 — толщина стенки.
Второй член в правой части этого выражения при малых деформациях стенки будет пренебрежимо мал по сравнению с первым членом. В этом случае
<417)
Подставив интегралы, определяемые соотношениями (4.12)-(4.17), в уравнение (4.10) и разделив результат на жг2, получим
— - _1 — ( _ 2f>vr° _ 2г°н (4 ig)
Dt р dx Z6ECT dt) pro
Здесь v = Q/(жгц) — средняя по сечению трубопровода скорость жидкости в данный момент времени.
При принятом масштабе времени I/со вторым членом в скобках в уравнении (4.18) допустимо пренебречь, если
С учетом условия (4.17) после вычисления интегралов и деления на ttt-q уравнение (4.11) можно привести к виду
Dp 2pro dp dv. „ Л/чЧ
1н + dt+Pdx~ (4'20)
Применив соотношение (см. гл. 1)
Представим уравнение (4.20) в виде
(L + ^^l + ^l = 0 (422)
в 6Ecr) dt дх [ ]
Таким образом, при рассмотренных допущениях уравнение (4.18) движения вязкой сжимаемой жидкости и уравнение
(4.22) неразрывности можно привести к следующим двум уравнениям соответственно:
£=-£!• (424)
|
Dv ~dt Toy касательного напряжения на стенке трубопровода можно |
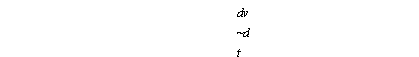
|
Шемся течении жидкости, когда — равно нулю, величину At |
![]() Где Втр — приведенный модуль объемной упругости жидкости, находящейся в трубопроводе с упругими стенками:
Где Втр — приведенный модуль объемной упругости жидкости, находящейся в трубопроводе с упругими стенками:
Найти по известной в гидромеханике формуле
Т0у = (4.26)
Здесь А — коэффициент гидравлического сопротивления трения трубопровода; уу — средняя по сечению трубопровода скорость установившегося течения жидкости.
Значения А зависят от числа Рейнольдса
Йе = . (4.27)
V
При установившемся ламинарном течении (Ле < 2300) коэффициент гидравлического сопротивления трения и касательное напряжение на стенке трубопровода можно вычислить достаточно просто, так как распределение местных скоростей по сечению трубопровода является параболическим (течение называют Гагена — Пуазейля). В этом случае А = 64/Ле и
Т0у = ^Ч. (4.28)
Принимая в каждый момент времени V = г;у, т. е. рассматривая нестационарное течение как сменяющиеся стационарные течения, которые происходят без изменения закона распределения местных скоростей, величину т0н в уравнении
(4.23) часто принимают квазистационарной и вычисляют ее по формуле (4.28). Однако такое приближенное представление закона трения при неустановившемся движении среды (см. гл. 2) не соответствует реальному течению. Согласно экспериментальным и теоретическим исследованиям, при неустановившемся движении вязкой среды изменяется распределение местных скоростей по сечению трубопровода и, следовательно, гидравлическое сопротивление трения трубопровода также изменяется. В связи с этим реальные значения тон отличаются от квазистационарных, причем различие может быть значительным. Чтобы учесть данную особенность нестационарных течений, величину тон следует представить функцией, в которой будет отражена для рассматриваемого процесса предыстория изменения структуры течения.
При высокочастотных колебаниях рабочих сред в трубопроводах характеристики нестационарного сопротивления трения ламинарных и турбулентных потоков сближаются, что позволяет использовать в расчетах формулу (4.28), предварительно умноженную на коэффициент, который зависит от частоты колебаний рабочей среды. После корректирования формула принимает вид
ГО
Где
Ае а = — + 0,4.
В соотношение для определения Гон входит безразмерная частота
О
(4'30)
Здесь и — угловая частота колебаний рабочей среды в трубопроводе.
По формуле (4.29) можно оценить, как возрастет сопротивление трения трубопровода вследствие нестационарности течения, вызванной колебаниями рабочей среды. Например, если диаметр проходного сечения трубопровода <1о = 2го равен 20 мм, а вязкость рабочей среды равна 12,5*10“[4] м2/с, то при частоте колебаний / = 16 Гц
2тг/г2
81/
При таком значении безразмерной частоты аеа = 5,4, соответственно во столько раз увеличится сопротивление трения трубопровода по сравнению с рассчитанным на основе предположения о квазистационар ной структуре ламинарного течения.
|
PAGE * MERGEFORMAT 161 |
![]() Уравнение (4.23) при тон = 0 вместе с уравнением (4.24) составляет систему уравнений, впервые опубликованную
Уравнение (4.23) при тон = 0 вместе с уравнением (4.24) составляет систему уравнений, впервые опубликованную
Н. Е. Жуковским в 1899 г. В таком виде уравнения описывают неустановившееся движение невязкой сжимаемой жидкости
в упругом трубопроводе. Расчеты колебательных процессов в трубопроводах гидроприводов без учета вязкости жидкости в некоторых случаях позволяют получить близкие к действительным наибольшие значения давлений в концевых сечениях трубопровода, но не позволяют определить интенсивность затухания колебаний по длине трубопровода и времени. При введении в расчет квазистационарного сопротивления трения трубопровода обеспечивается только приближенная оценка влияния вязкости среды на затухание колебательных процессов, причем при резонансных частотах значения амплитуд давления, вычисленные как без учета вязкости среды, так и с учетом квазистационарного сопротивления трения трубопровода, могут оказаться значительно больше рассчитанных с учетом реального увеличения сопротивления трения.
Уравнения (4.23) и (4.24) во всех рассмотренных выше случаях описывают неустановившееся течение сжимаемой рабочей среды при распределенных по длине трубопровода параметрах. Эти уравнения при ограниченных изменениях давлений и скоростей среды могут быть также применены в математических моделях пневмоприводов. Уравнения (4.1), (4.2) и (4.23), (4.24) образуют математическую модель гидро - или пневмопривода с распределенными параметрами, которая отличается от модели с сосредоточенными параметрами тем, что в нее кроме обыкновенных дифференциальных уравнений входят уравнения в частных производных. Системы, математические модели которых должны быть представлены в распределенных параметрах, обладают рядом особенностей, не проявляющихся в системах, описание которых может быть дано в сосредоточенных параметрах. Например, системы с распределенными параметрами теоретически имеют бесконечное число резонансных частот. У таких систем могут быть перемежающиеся области устойчивых и неустойчивых режимов работы, а также вследствие возникновения гидравлических ударов могут разрушаться трубопроводы и подключенные к ним устройства гидроприводов.