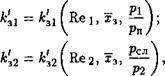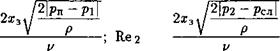Механика гидро - и пневмоприводов
Нелинейная математическая модель силовой части гидропривода с дроссельным регулированием
С помощью структурного представления математических моделей систем можно решать различные задачи динамики гидро - и пневмоприводов. Однако практически невозможно, да и вряд ли необходимо, пытаться рассмотреть даже основные задачи в приложении ко всем видам гидро - и пневмоприводов. Целесообразнее на примерах наиболее распространенных конструкций приводов освоить достаточно общую методику математического моделирования и построения структурных схем такого класса управляемых систем, которые объединяет наличие в качестве рабочей среды жидкости или газа. При таком подходе к математическому моделированию приводов выделим в любом приводе силовую и управляющие части. К силовой части отнесем исполнительный гидро - или пневмодвигатель с регулирующим движение его выходного звена устройством. Воздействующие на это устройство аппараты, а также формирующие сигналы управления датчики и приборы отнесем к управляющей части. Сначала рассмотрим гидроприводы, рабочей средой для которых служат малосжимаемые жидкости, а затем пневмоприводы, что позволяет показать, как влияет увеличение сжимаемости рабочей среды (воздуха или другого газа) на динамику приводов.
|
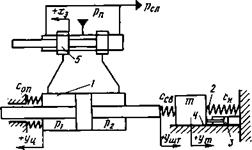
Рис. 5.1. Схема силовой части гидропривода с дроссельным регулированием |
Для математического моделирования воспользуемся расчетной схемой, изображенной на рис. 5.1. На схеме гидроцилиндр 1 с проходным штоком имеет внешнюю опору жесткостью соп - Нагрузка на выходное звено (шток гидроцилиндра) принята инерционной, позиционной и в виде трения. Первую из перечисленных нагрузок создает перемещаемое выходным звеном тело массой га, вторая — условно представлена пружиной 2 с нулевым натяжением при среднем положении поршня гидроцилиндра. Нагрузку от действия вязкого трения имитирует гидравлический демпфер 3, а от сухого трения — граница 4 плоскости, по которой без смазки перемещается тело массой га.
Жесткость связи тела массой га со штоком гидроцилиндра обозначена ссв. Положительным выбрано перемещение х3 золотника, соответствующее положительному перемещению штока гидроцилиндра (на схеме — вправо).
Математическое описание динамических процессов в таком исполнительном гидродвигателе начнем с уравнения движения тела массой га:
|
Га- |
|
Л2 |
|
— Ссв(2/шт — Ут) ~ снУтп ~ - Ргр> |
|
|
Где Рхр — сила, вызванная действием вязкого и сухого трения; в общем случае является нелинейной функцией скорости ит = = т. е.
Рт р = - Ртр('ит)• (5-2)
Уравнение движения выходного звена (штока гидроцилиндра) запишем в виде
Тп ^2 “ &1Р1 — *?2Р2 ~ ссв(Ушт — Ут) — ^тр. ц> (5*3)
Где тп — суммарная масса поршня и штока гидроцилиндра; 5^1 и £2 — площади поршня в левой и правой полостях гидроцилиндра, в которых давления жидкости равны р и р2 соответственно; РТр. ц — сила трения в уплотнениях гидроцилиндра. При смешанном трении в уплотнениях
^тр. ц — - Ртр. ц(^шт> ^ц)> (5*4)
Где ишт = <1утт1<И уц = ([уц/вР, уц — перемещение гидроцилиндра на упругой опоре.
В свою очередь величина входит в уравнение
Тц ^2 “ ” &2Р2 ~ сопЗ/ц — Ргр. Ц) (5*5)
Где гац — масса гидроцилиндра.
При смещении золотника в направлении +х3 в левую полость гидроцилиндра поступает жидкость с массовым расходом
£1=^31, (5-6)
Где р — плотность жидкости; — объемный расход жидкости, поступающей в левую полость гидроцилиндра.
Согласно условию неразрывности течения, имеем
<*(У1 + У1Л) , Уг + У^йр!
Где Всм 1 — модуль объемной упругости находящейся в левой полости гидроцилиндра смеси жидкости с воздухом; У — объем левой полости гидроцилиндра; Ул — объем канала, соединяющего левую полость гидроцилиндра с золотником.
Уравнение (5.7) и используемое далее аналогичное уравнение для правой полости гидроцилиндра записаны в предположении одновременного изменения давления во всех сечениях каналов (гидролиний), соединяющих гидроцилиндр с золотником, т. е. в сосредоточенных параметрах. При этом инерция жидкости не учитывается, а гидравлическое сопротивление каналов учтено в коэффициенте расхода золотника.
Вследствие перемещения поршня гидроцилиндра и перемещения самого гидроцилиндра, вызванного упругостью опоры, объем У будет переменной величиной, поэтому
^1 = *01 + + *^13/ц> (^-®)
Где Уо1 — объем левой полости гидроцилиндра при начальном положении поршня, от которого измерены значения ушт И Уц.
После подстановки величины У из уравнения (5.8) в уравнение (5.7) и сокращения на р получаем
П - с шт I с
<1уп Уг + У1л <1р1 вэ1 = 1 ~лГ (5'9)
Аналогично находим уравнение объемного расхода жидкости, вытекающей из правой полости гидроцилиндра
^ с ^3/шт, с ^3/ц ^2 + ^2л^Р2 /с 1ГЛ
Ц? з2 = *>2—^7“ + *>2 - т-------- Б----------- ЗГ’ V5-10)
Аь аь псм 2 их
Где У2 — объем правой полости гидроцилиндра, который уменьшается при движении поршня в направлении Н-2/шт; У2Л — объем канала, соединяющего правую полость гидроцилиндра с ЗОЛОТНИКОМ; Всм2 — модуль объемной упругости смеси жидкости и воздуха, вытесняемой из правой полости гидроцилиндра.
Входящие в уравнения (5.9) и (5.10) модули объемной упругости можно определить по соотношению
= ,4..ВВ /В ' <5Л1>
1 I аВ1^Ж|/^В
Где г = 1 для полости с давлением р, г = 2 для полости с давлением р2-
Объемное ав,- = Уъ/Усм содержание воздуха в жидкости может быть различным в каждой полости гидроцилиндра вследствие разной продолжительности процессов растворения и выделения воздуха в жидкости.
Расходы жидкости фз1 и ф32 через окна, открытые кромками золотника, описываются функциями вида (3.83). Чтобы
связать изменения этих расходов с перемещениями золотника и давлениями в полостях гидроцилиндра, представим функции следующими выражениями:
<Эз1 = - pi|sign(pn - Pi); (5.12)
Q32 — кз2Х3л/р2 — Рсл| sign(p2 — Рсл)> (5.13)
Где к'з1 и А? з2 — удельные (отнесенные к единице перемещения золотника) проводимости окон, открытых при смещении золотника от среднего положения.
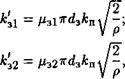 В формулах (5.12) и (5.13) корни квадратные извлекаются из модулей разности давлений, что исключает появления мнимых значений расходов, а возможное изменение направлений течений жидкости учитывается функцией sign (...)• Удельные проводимости окон определяются соотношениями
В формулах (5.12) и (5.13) корни квадратные извлекаются из модулей разности давлений, что исключает появления мнимых значений расходов, а возможное изменение направлений течений жидкости учитывается функцией sign (...)• Удельные проводимости окон определяются соотношениями
(5.14)
(5.15)
Где кп = Ьок/тг^з — коэффициент полноты использования периметра втулки золотника при размещении в ней окон.
Согласно формулам (5.14) и (5.15), удельные проводимости окон, через которые жидкость поступает в гидроцилиндр, могут отличаться от удельных проводимостей окон, через которые жидкость вытекает из гидроцилиндра. Это вызвано различными значениями коэффициентов /х31 и /х32, зависящих от направления течения жидкости через окна золотникового устройства. Коэффициенты расхода определяют экспериментальным путем. Наиболее полное представление об удельных проводимостях золотникового устройства можно получить, если результаты экспериментов обработаны в зависимости от значений числа Рейнольдса, относительного перемещения золотника и относительных значений давления после окон, т. е. имеют вид
|
|
|
|
= хъ/хз шах — безразмерное смещение золотника от среднего положения; хзтах — максимальное смещение золотника в одну сторону.
Все приведенные выше уравнения получены при хъ > О, Ушт >0. В случае х3 < 0 необходимо в уравнениях поменять местами давления р и р2, так как теперь правая полость гидроцилиндра будет соединена с каналом, в котором давление рП) а левая полость гидроцилиндра — с каналом, в котором давление рсл. С учетом этих перестановок членов, соответствующих смещению золотника в разные стороны от среднего положения, после несложных преобразований уравнений (5.1)—(5.15) нелинейную математическую модель силовой части гидропривода с дроссельным регулированием можно описать следующей системой дифференциальных уравнений в форме Коши:
<1у1
ТП
|
Ссв + СН 1 п Утл ^тр> 777 777 |
![]() БТ = ”т;
БТ = ”т;
Ссв
|
777 — |
![]() Л - —Ушт <1ушт
Л - —Ушт <1ушт
*$1 $2 Ссв, Ссв 1 ту
~Т, — Р1 Р2 Ушт Н Утп ~ ^тр. ц!
(И 777 777 777 777 777
|
^Уи <И йп “Л При я3 > 0 |
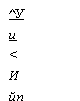
|
= V: |
![]() Ц *^1 $2 соп 1 т>
Ц *^1 $2 соп 1 т>
А+ “ ^ Р1 ~ Р2 ~ 3/ц “ ~ гр. ц!
777 777 777 777
|
^Р1 <и |
![]() I3 1 аг3/|Рп-Р1| з1§п(р„ - Р1)- п + Пл
I3 1 аг3/|Рп-Р1| з1§п(р„ - Р1)- п + Пл
■^1 -®см 1 ^1 - бсм 1
|
Ц) |
~<м ~ ~ у22+Хз^Р2 ~ Рсл^^Р2 ~ Рсл)+
. $2ВСм2 , ^Всмг
Т/ I т/ ^шт “Г ту, ту %,
^2 + л ^2 + ^2 л
При х3 < О
^ = ~'^1^1л 13 ^Р1 — ^сл I ®1бп(Р1 “ Рсл)+
, *$1 В СМ 1 , *^1 В см 1
^Р2 ^з3^см2 А Г. / ч
Л-=угп^; 1,л/|!>л - и| 818п(р" - и)-
52£
См2 ■^2-Всм2
^2 + ^2л 1,ШТ ^2 + ^/“’
Где = ^з35 Лз2 = *з4-
Данную систему дифференциальных уравнений необходимо дополнить функциями (5.2) и (5.4), а также функциями, которые определяют проводимости окон, открываемых кромками золотника. Кроме того, следует указать минимальные допустимые давления р и р2> исключающие кавитацию в гидроприводе. Для изучения основных динамических свойств гидропривода с дроссельным регулированием эта модель слишком сложна. С этой целью целесообразно применить более простую, но в то же время достаточно достоверную при ряде ограничений математическую модель гидропривода.