Механика гидро - и пневмоприводов
Линеаризация уравнений и структурные схемы математических моделей
Математическое описание процессов в гидро - и пневмоприводах, а также в источниках энергопитания приводов, как показано в предыдущих главах, связано с использованием нелинейных функций. Вследствие этого основу математических моделей составляют нелинейные дифференциальные уравнения (4.1) и (4.2), с помощью которых исследование систем в большинстве случаев можно выполнить численными методами, так как аналитические методы применимы при ряде ограничений на порядок дифференциальных уравнений и вид содержащихся в них нелинейностей. Возможности численных методов в современных исследованиях любых систем несоизмеримо выросли по сравнению с аналитическими методами. Однако результаты численных исследований часто оказываются недостаточными при выводе общих закономерностей, определяющих важные для практики свойства систем. В то же время аналитические методы исследования линейных математических моделей позволяют получать вполне обобщенные результаты, они подробно разработаны в математике и в тех дисциплинах, которые используют при решении различных задач механики гидро - и пневмоприводов.
Понятие линейная математическая модель означает наличие пропорциональности между внешними воздействиями на систему и вызванными ими изменениями переменных состояния. Важное свойство линейных систем состоит в том, что рассчитанные при отдельных воздействиях процессы после суммирования определяют процесс, возникающий в результате всех этих воздействий. Данное свойство является одним из примеров принципа суперпозиции решений линейных дифференциальных уравнений, заменяющих в математической модели нелинейные дифференциальные уравнения. Такая замена исходной нелинейной математической модели реальной системы приближенной линейной моделью может быть выполнена в ограниченной области переменных состояния и при ограниченных внешних воздействиях. Кроме того, необходимо, чтобы характеристики элементов и системы в целом позволяли
|
, д{ Х +7Г Хо, и0 ди |
|
И' Хо. ио |
|
Дх |
|
(4.31) (4.32) Если нелинейные функции в правых частях уравнений (4.31) и (4.32) раскладываются в ряд Тейлора в окрестности хо, ио, то, пренебрегая членами с отклонениями в степени выше первой, эти функции приближенно представляют в виде Г(хо + х', ио + и', *) = i(■x. о, и0, г)+ Д{ |
|
Лео йх! , . . 1Г + ИГ = ^х° + х ’ ио + и. 0; Уо + у' = 8(хо + х', и0 + и', *). |
|
|
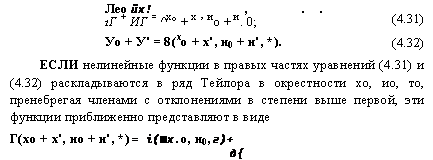 |
|
|
|
|
|
|
|
И' Х0,и0 |
![]()
|
(4.34) |
![]() Х0,и0 дп
Х0,и0 дп
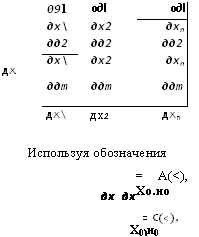
Входящие в функции (4.33) и (4.34) якобианы определяют по следующим формулам:
|
Дх2 Используя обозначения дх дх |
|
= А(<), Хо. ио |
|
= С(<), Х0)и0 |
|
|
Дх |
|
Дх |
|
Дхп |
|
Дм Д% 0и |
|
= В((), Х0,и0 = П((), Хо, и0 |
 |
|
|
||||||||||||
|
||||||||||||||
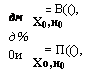 |
||||||||||||||
Из уравнений (4.31) и (4.32) выделяют уравнения, описывающие изменение исходного состояния системы в малых отклонениях:
^- = А(<)х' + В(<)и' (4.35)
У' = С(<) х' + Б(<) и', (4.36)
Где А(*), В(*), С(*) и Б(<) — матрицы, элементы которых являются заданными функциями времени.
При зависящих от времени коэффициентах (матрицах) уравнений (4.35) и (4.36) системы, соответствующие такому математическому описанию, называют нестационарными. Если коэффициенты постоянные, то системы называют стационарными. Для таких систем эти уравнения имеют вид:
И-х1
— = Ах' + Ви' (4.37)
А%
И
У' = Сх' + Би' (4.38)
Здесь А, В, С и Ю — матрицы с постоянными элементами.
Рассмотренный метод линеаризации дифференциальных уравнений нельзя применять в случае, когда нелинейные функции не могут быть разложены в ряд Тейлора из-за наличия
Разрывов в окрестности исходного состояния системы. В таких случаях функции называют существенно нелинейными и для линеаризации либо, если это возможно, выбирают другие исходные состояния системы, либо применяют другие методы исследования, два из которых кратко изложены в главе 6 при анализе причин возникновения автоколебаний в гидроприводах. Линеаризованные математические модели систем получают также путем предварительной аппроксимации нелинейных функций, принимая те или иные допущения относительно свойств и характеристик систем.
Математическую модель исследуемой системы можно представить не только уравнениями, но и в виде схемы, показывающей вид вычислительных операций в модели, связи между ее блоками и приложенные к системе внешние воздействия. Такие схемы называют структурными. Линейной математической модели системы с векторно-матричными уравнениями
(4.35) и (4.36) соответствует структурная схема, изображенная на рис. 4.1.
|
Щ |
![]()
|
Т |
![]()
|
Ч |
![]()
|
*(*} Рис. 4.1. Структурная схема линейной математической модели системы с вектор но-матричными уравнениями На схеме для упрощения записи у переменных не указаны штрихи, которыми при выводе уравнений были отмечены отклонения переменных от своих исходных значений. Необходимость в дополнительных индексах вообще отпадает, если исходные значения переменных можно принять за начало отсчета их изменения. Эта возможность в дальнейшем используется при составлении линеаризованных моделей гидро - и пнев- |
Моприводов. Стрелки, обозначенные на схеме двойными линиями, соответствуют каналам, передающим сигналы с информацией о значениях векторных переменных. Внутри прямоугольников, которыми показаны основные блоки, записаны матрицы-коэффициенты уравнений и символ интегрирования для вычисления векторной переменной х. В тех местах схемы, где должно происходить алгебраическое суммирование нескольких сигналов, введены кружки с указанными в них знаками сложения или вычитания сигналов. Разветвление стрелок означает, что сигналы без изменения своих значений передаются нескольким блокам.
Чтобы выделить характерные свойства отдельных звеньев, участвующих в формировании и передаче сигналов в системе, применяют математические модели, основой которых являются уравнения типа вход-выход. При этом широко используют линейные дифференциальные уравнения с постоянными коэффициентами:
Dny dn~^y
And^ + an~1di^ + +аоУ =
= 6m—+ 6m_ i^r+ +b0u. (4.39)
Вводя символ дифференцирования pt = d/dt, уравнение (4.39) записывают в символической форме
D(pt)y = M(pt)u, (4.40)
Где и — входная величина (входной сигнал); у — выходная величина (выходной сигнал);
D{Pi) = QnPt + On-ip"-1 + + «о; (4.41)
M(Pt) = Ьтр? + 1 + + bo. (4.42)
Выражения (4.41) и (4.42) называют собственным оператором системы или звена и оператором воздействия на систему или на ее звено соответственно.
Уравнение (4.40) можно представить также в виде
У = У(рг)и. (4.43)
В уравнении (4.43) связь между зависящими от времени входной и выходной величинами определяет передаточная функция
= Ш' (4'44)
Которая показывает, какие математические операции необходимо выполнить с функцией и = и(/), чтобы найти функцию
У = з/(/). Так как операторы (4.41) и (4.42) непосредственно
Следуют из дифференциального уравнения (4.39), описывающего динамические состояния системы или какого-либо из ее звеньев, передаточная функция отражает присущие реальным устройствам свойства, учитываемые при составлении математических моделей этих устройств.
С помощью передаточной функции (4.44) получают алгоритмы для расчетов на аналоговых и цифровых вычислительных машинах. При аналитических исследованиях указываемые передаточной функцией математические действия выполняются проще, если применить методы операционного исчисления. Эти методы основаны на интегральном преобразовании Лапласа:
Оо
^(5) = I е~3*/{г)(Н. (4.45)
Преобразование (4.45) переводит функцию-оригинал /(/) действительного переменного в функцию-изображение ^(з) комплексного переменного 5. Соответствие между оригиналами и изображениями обозначают по-разному, часто для этого используют выражение
Применив преобразование Лапласа и его свойства, дифференциальное уравнение (4.39) при нулевых начальных условиях можно представить в виде
(ая5п + ая_15п 1 + -|-ао)У(5) =
= (Ьтзгп + Ьт-1зт-1+ +Ьо)и{з), (4.47)
Где у(<) ==’ У ($), и(<) = II (з). Отношение У (а) к II (й) определяет передаточную функцию в изображениях:
= *т»та + + ■ - + *0 (4 48)
Апзп + ап_15п_1 + + а0
Сравнивая формулы (4.44) и (4.48), легко заметить, что передаточную функцию (4.48) формально можно получить непосредственно из уравнения (4.39), подставив в него 5 = <1/<И. Основанием для такой замены служит изоморфизм поля операторов в пространстве действительных переменных и в пространстве изображений по Лапласу.
Вычисляя для заданной функции и(£) изображение и (в) и используя передаточную функцию И^з), изображение выходной величины можно найти по соотношению
У(з) = ]У(зЩз). (4.49)
Для вычисления функции-оригинала по известному изображению применяют теоремы Хевисайда или таблицы соответствия оригиналов и изображений. Функция у(ї) описывает отклик (реакцию) звена или системы на входное воздействие «(<).
Если входная величина изменяется в соответствии с гармоническим законом, то необходимость в обратном преобразовании изображения выходной величины отпадает. В этом случае в передаточную функцию подставляют 5 = У а;, У = = у/— Полученную в результате такой подстановки комплексную функцию ¥(3и) называют амплитудно-фазовой частотной характеристикой (АФЧХ) системы или звена. Она определяет отношение амплитуд выходной аВЫх и входной аъх
Величин, а также смещение ір по фазе между этими величинами в зависимости от частоты и. Для вычисления используют формулу
УУЦи) = А(ы)е^И5 (4.50)
Где А(и) = авых(и>)/авх(и;) — относительная амплитуда.
Из формулы (4.50) следует, что А(и) = тосі ¥^и) — модуль и у>(и>) = — аргумент комплексной функции Графики А(и) и <р(и) называют амплитудной и
Фазовой частотными характеристиками звена или системы. Эти характеристики обычно строят в логарифмических координатах, измеряя 20^ А(и) = Ь(и) в децибелах, (р(и) в радианах в секунду, и называют их логарифмической амплитудной характеристикой (ЛАХ) и логарифмической фазовой характеристикой (ЛФХ) соответственно. Частотные характеристики широко применяют при исследованиях и проектировании разнообразных систем, представленных структурными схемами, звенья которых могут быть соединены последовательно, параллельно и в виде контуров с обратными связями.
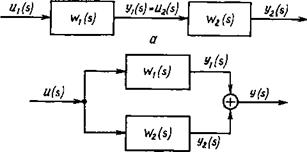
При последовательном соединении звеньев выходная величина (сигнал) предыдущего звена служит входной величиной (сигналом) для последующего звена (рис. 4.2, а). Передаточную функцию У(в) двух последовательно включенных звеньев можно получить с помощью передаточных функций этих звеньев
ИМ*) = У^/и^з) и 1У2(*) = У2(*)/ад> где Е/г(5) = Уі(5)- Из приведенных соотношений следует, что
Если последовательно соединено п звеньев, то
П
И^а) = Ц И'ї(а). (4.51)
1=1
Амплитудно-фазовая частотная характеристика ¥^и) цепи, составленной из п последовательно включенных звеньев, определяется согласно формуле (4.51) путем перемножения АФЧХ отдельных звеньев, поэтому
П
АИ = ПАіМі (4.52)
1=1 п
І=1
|
Б |
![]()
|
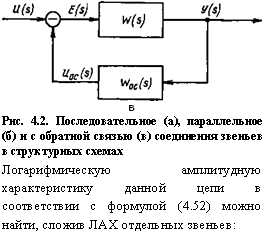
В Рис. 4.2. Последовательное (а), параллельное (б) и с обратной связью (в) соединения звеньев в структурных схемах Логарифмическую амплитудную характеристику данной цепи в соответствии с формулой (4.52) можно найти, сложив ЛАХ отдельных звеньев: |
 Где А(и) и ц>(и) — амплитудная и фазовая частотные характеристики цепи последовательно включенных звеньев.
Где А(и) и ц>(и) — амплитудная и фазовая частотные характеристики цепи последовательно включенных звеньев.
L{u) = ^Li{u), (4.54)
T=l
Где L{u) = 201gA(w), Li(u) = 201gA;(o>).
Логарифмическую фазовую характеристику цепи по-прежнему определяет формула (4.53), только в логарифмическом масштабе следует брать значения частоты и.
При параллельном соединении звеньев входные величины (сигналы) имеют одинаковые значения, а выходные величины (сигналы) суммируются. В случае двух звеньев (рис. 4.2, б):
Y(*) = Yi(e) + Y2(*); Y1(S) = W1(S)U(Sy,
Y2(s) = W2(s)U(s)] W(s) = щ = Wi(s) + W2(a).
Откуда следует, что передаточная функция п параллельно соединенных звеньев является суммой передаточных функций этих звеньев, т. е.
П
W(a) = ^(s)- (4-55)
1=1
Амплитудно-фазовую частотную характеристику параллельно соединенных звеньев можно вычислить по правилу сложения комплексных величин:
П п
W(ju) = £ + j Y, Qi(v), (4.56)
1=1 »'=1
Где Pi(u>) и jQi(u) — вещественная и мнимая части АФЧХ каждого звена.
Логарифмические амплитудная и фазовая частотные характеристики параллельно соединенных звеньев вычисляют с учетом того, что А(и>) = mod W(ju), <р{и) = ^TgW(ju).
Замкнутый обратной связью контур состоит из прямой цепи звеньев и цепи звеньев в обратной связи, которая чаще всего бывает отрицательной, но может быть и положительной. Приведенная на рис. 4.2,в структурная схема показывает, что
E(S)=U(s)^U0.c(s), (4.57)
Uo. c(s) = W0.c(s)Y(s), (4.58)
Y(s) = W(s)E(s). (4.59)
Используя соотношения (4.57)-(4.59), нетрудно получить передаточную функцию контура с обратной связью
Фм. т____________ ш________________ (4 ев)
И(з) ~ 1 ± И'(»)И'„.с(5) • ( Щ
В передаточной функции (4.60) знак соответствует отрицательной обратной связи, при положительной обратной связи следует принять знак
Соотношения (4.57)-(4.59) позволяют найти также передаточную функцию для вычисления ошибки, изображение которой £(з):
= ОД = 1 + ^(а)^0.с(а)' (4'61)
Амплитудно-фазовую частотную характеристику контура с обратной связью можно рассчитать по формуле (4.60) после подстановки в нее в = Зи>. При этом используют правила вычислений комплексных величин и программы для расчетов систем управления.
Рассмотренные преобразования передаточных функций позволяют упростить приведение исходной структурной схемы к более удобному для расчета виду. С той же целью могут быть выполнены преобразования участков структурных
Схем путем переноса узлов суммирования и разветвления сигналов, причем преобразования структурных схем не должны влиять на результаты расчета процессов в системе. Примеры таких эквивалентных преобразований участков структурных схем даны на рис. 4.3, в левой половине которого показаны первоначальные расположения узлов, в правой — после их переноса.
Заметим, что структурные схемы, построенные по передаточным функциям, которые были получены в изображениях по Лапласу, применимы только для расчетов и исследований линейных систем. Если математическая модель системы содержит нелинейности, которые нельзя устранить описанными выше методами, то при построении структурной схемы системы следует рассматривать передаточные функции в форме (4.44) и, соответственно, расчеты выполнять с учетом того, что указанные на схеме переменные являются функциями времени, а не их изображениями.
|
Ф) |
|
У( Ф)^ Ф) |
|
|
У(&) Ф) |
|
УМ |
|
|
*(*) |
|
2(5) |
 |
||||||||||
|
||||||||||
|
||||||||||
|
||||||||||
|
||||||||||
|
||||||||||
|
||||||||||
|
||||||||||
|
||||||||||
|
|||||||||||
|
|||||||||||
|
|||||||||||
|
|||||||||||
|
|||||||||||
|
|||||||||||
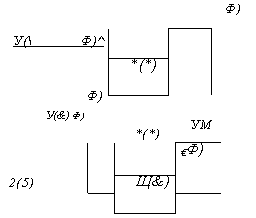
Рис. 4.3. Примеры эквивалентных преобразований участков структурных схем
