АВТОМАТИЗИРОВАННЫЙ ЭЛЕКТРОПРИВОД В ПРОКАТНОМ ПРОИЗВОДСТВЕ
ЕСТЕСТВЕННЫЕ МЕХАНИЧЕСКИЕ ХАРАКТЕРИСТИКИ ДВИГАТЕЛЯ НЕЗАВИСИМОГО ВОЗБУЖДЕНИЯ
Аналитическое выражение механической характеристики двигателя постоянного тока получается из уравнения (II 5) электрического равновесия якорной цепи при установившемся режиме работы
£/ = £■ + /я/?я = кЕФп - j - /я/?я,
|
откуда U /я/?я |
Подставляя в это уравнение значение тока якоря из формулы (11.11), получим
U Яя М„ (11.43)
~ кЕФ ЬЕкМфг
Следовательно, в уравнение механической характеристики входит электромагнитный момент. Как отмечалось выше, при практических расчетах можно считать, что М «=< Ма. В случае, если магнитный поток у двигателя постоянен (Ф =* const), уравнение механической характеристики упрощается:
п = — — М = — - -£=- /я (II 44)
СЕ СЕСМ СЕ СЕ
Уравнение механической характеристики может быть записано-в виде
п = п0 — Ап, - (11.45)
U U
тде п0 = ^ф — — скорость идеального холостого хода двигателя (при М = 0 и = 0);
MR I R
^п = кЕкмФ* = ТІ5" — пеРепаД скорости вращения при данном моменте М и данном сопротивлении якоря RA. Уравнение механической характеристики можно также получить из структурной схемы двигателя как объ'екта регулирования в виде статической характеристики замкнутой системы.
Для схемы, представленной на рис. 15, в, скорость двигателя п определяется двумя входными сигналами - управляющим воздействием U и возмущающим (—/с). Рассмотрим действие каждого входного сигнала отдельно, а регулирующий эффект от обоих сигналов получим, применив принцип, наложения.
Передаточная функция для управляющего воздействия U (1С = 0)
Wu(p) = у(р) = гэг„р*+дгмр+ 1 • (И-46)
Для установившегося режима работы
|
. (11.47) |
пи U
где пи — — = ft о — скорость идеального холостого хода.
^Е
Передаточная функция для возмущения (—/с) (U = 0)
|
(II 49) (II 50) (II 51) |
|
/с’ |
|
Ля/с |
|
Ля /я |
|
— — Ап |
|
Пі —----- 7— С k с |
|
э£ Я С Результирующий эффект от обоих сш палов IL ЯяТя = JL _ с Г. С, с, сгс„ |
|
Ап, |
|
п = пи + m |
|
Пп |
|
т е получили уравнение механической характеристики Если уравнения механической характеристики получены для поминальных условий рабшы двіиаіслл » оиюшспин его _>лек- |
|
|
|
п По |
|
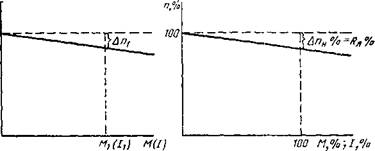
Рис 17 Естественные механические характеристики дш гате ія незаиисимого возбуждения |
|
трических параметров, то имеем ‘естественные механические характеристики (рис 17). Уравнения (II 42) и (И 43) показывают, что зависимости п = f (М) и п — f (/) выражаются прямой линиеи и скорость двигателя с увеличением нагрузки падает (см рис 17, а) Уравнение механической характеристики в относительных единицах (см рис. 17, б) получают делением уравнения (II 44) на п0- М = 1-------- r7^L_M-4L - - I—-#-• Rn мн |
|
п |
|
// MJr UhCM и |
|
1 |
|
1 |
|
(II 52) Выражая сопротивление и момент в процентах, получим Rn _ М , и п/ л „ л/ |
|
ітї'ж) 10()= 10°—""/» |
|
Для случая, когда М = Мн, /?я% == Дл„ % = ($%. Для двигателя независимого возбуждения при моменте двигателя, равном номинальному, и при номинальном потоке отно- |
сительное падение скорости равно относительному значению сопротивления якоря. Двигатели независимого возбуждения характеризуются малой величиной /?п, и значение /я/?й мало по сравнению с UH. Величина Апи% = Р% для таких двигателей составляет 2—8%, т. е. естественная механическая характеристика двигателя независимого возбуждения жесткая.