Распад струй и образование капель
Истечение струй из отверстий разбрызгивающего устройства и их последующий распад на капли является сложным гидродинамическим процессом.
Определению размера образующихся при дроблении струи капель посвящен ряд теоретических и экспериментальных работ [ПО, 111]. При выходе из отверстия под действием шероховатостей его наружной кромки на струю жидкости накладываются небольшие возмущения. На характер возмущений влияют также следующие факторы: отклонение выходного отверстия от правильной цилиндрической формы; завихрения в сопле; наличие пузырьков воздуха в струе; степень сжатия струи ит. п.
Под воздействием возмущений частицы жидкости, находящиеся на поверхности струи, испытывают различного рода смещения, что приводит к деформации струи. С другой стороны, силы поверхностного натяжения стремятся сократить общую поверхность струи: «возмущенные» частицы жидкости возвращаются в прежнее положение. В результате взаимодействия внешних возмущений и сил поверхностного натяжения жидкости на поверхности струи возникают колебания. По мере истечения амплитуда колебаний увеличивается и струя распадается на отдельные части.
Процесс распада струи в общем случае описывается нелинейными гидродинамическими уравнениями, аналитическое решение которых не представляется возможным. Поэтому при решении этой задачи обычно исходят из метода малых возмущений. Этот метод позволяет линеаризовать исходные уравнения, рассмотреть условия неустойчивости струи и определить длину волны максимальной неустойчивости (А,).
Рэлей (цитируется по [ПО]) получил значение А, зависящее только от диаметра струи {(1, ):
А=4,5ЫС. (5.1)
Вебер рассмотрел процесс распада струн на капли с учетом физических свойств жидкости и получил следующую зависимость'
А=ш1с {2 [ 1 + (£р2ж/ср „(Іс) */2]} '/г, (5.2)
где Цж — динамическая вязкость; р*— плотность жидкости.
завнснмость для определения размера образующихся капель:
 dK/dc=(3/2ty<ic),/3. (5.4)
dK/dc=(3/2ty<ic),/3. (5.4)
Подставляя в (5.4) значения K/dc из выражений (5.1) — (5.3), получили соответствующие формулы для расчета диаметра капель:
rfK=l,89rfc, (5.5)
d„= l,87rfc [1 + (gfi2Japmdc) */2] "s, (5.6)
dx=2,0€idc exp(— 0,0519pWe)M00M. (5.7)
Для определения среднего диаметра гранул аммиачной селитры рекомендована [112] следующая зависимость:
rfcp=2,4rfcM0 (IH exp (— 0,052pWe). (5.8)
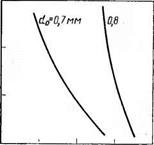
На рис. 5.1 представлены типичные кривые распределения гранул аммиачной селитры по размерам, полученные при гранулировании плава концентрацией 99,5% NH4N03 в статическом грануляторе в зависимости от диаметра отверстий.
Авторами работ [112, 113] отмечается несущественность влияния статического напора жидкости (или скорости истечения) на размер образующихся капель (гранул). Так, при изменении статического напора плава аммиачной селитры от 0,5 до 2,0 м средний диаметр гранул увеличивается лишь на 0.1 мм.
![]() йср, мм
йср, мм
![]()
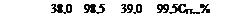
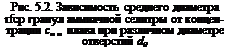
 V
V
1,5
Рис. 5.1. Интегральные кривые распределения гранул F(d) аммиачной селит-
ры по размерам d при различном диаметре отверстия d0
Размер образующихся гранул в значительной мере зависит от концентрации плава. Как правило, с уменьшением концентрации пдава средний размер гранул увеличивается (рис. 5.2), что объясняется изменением физических свойств плава.
В ряде работ [111, 113] показано, что наложение на струю внешних возмущений (вибрации) обеспечивает получение более однородных по размеру гранул. Базируясь на результатах опытов, проведенных с водой и плавом аммиачной селитры, предложен [111] следующий диапазон частот колебаний струи (образования капель):
/=«о/ [ (3,54-8) doe*/*]. (5.9)
где «о — начальная скорость струи; е — коэффициент сжатия струи.
Средний размер капель, полученных при гранулировании с наложением вибраций на истекающие струи с точностью 10%, может быть рассчитан по уравнению
dK— (,5еРеив/[)і/3. (5.10)
Важное значение для описания траектории движения капель (гранул) имеет начальная скорость их движения в момент отрыва. Величина этой скорости определена экспериментально в зависимости от угла вылета струи [П2], в результате чего получена расчетная формула:
Чк/и0= 1 — 0,22 sin etc, (5.11)
где «к — скорость движения капель в момент отрыва.