Механика гидро - и пневмоприводов
Линейная математическая модель силовой части гидропривода с дроссельным регулированием
Для упрощения рассмотренной выше системы дифференциальных уравнений воспользуемся, прежде всего, тем, что у реальных гидроприводов геометрические параметры левой и правой половин схемы при среднем положении поршня гидроцилиндра часто имеют близкие значения. В таких случаях можно принять: = Б2 = 5П, = У2 = Уо, Ул = У2л = УЛ9
У — У —У —У — У
*3 1 “ з2 “ з3 “ з4 “ *3-
При динамических процессах, которые происходят со скоростями, превышающими скорости растворения и выделения газа в жидкости, значение модуля Всм объемной упругости смеси примем равным значению модуля Вж объемной упругости жидкости, которое не зависит от давления, но вычислено с учетом постоянного газосодержания в жидкости при среднем уровне давлений в полостях гидроцилиндра.
Пренебрегая, кроме того, сухим трением в нагрузке на выходное звено и учитывая знаки в уравнении (5.1), представим силу вязкого трения в виде
(5.16)
|
(5.17) |
![]() Наконец, нелинейные функции (5.12) и (5.13) заменим уравнением аппроксимированной расходно-перепадной характеристики золотникового устройства (см. гл. 3)
Наконец, нелинейные функции (5.12) и (5.13) заменим уравнением аппроксимированной расходно-перепадной характеристики золотникового устройства (см. гл. 3)
Фз — КдхХ3 — К(2рРНу
Где рн = Р1 - Р2-
![]() Заметим, что коэффициенты уравнения (5.17) нельзя вычислить как коэффициенты первых членов ряда Тейлора, поскольку исходная функция (рис. 5.2)
Заметим, что коэффициенты уравнения (5.17) нельзя вычислить как коэффициенты первых членов ряда Тейлора, поскольку исходная функция (рис. 5.2)
(5.18)
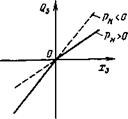 В окрестности точки, соответствующей равновесию (рн = О, <2з = 0) силовой части гидропривода, имеет разрыв по первым производным. Во всех остальных точках расходно-перепадной характеристики коэффициенты Кдх и Кдр определяются формулами:
В окрестности точки, соответствующей равновесию (рн = О, <2з = 0) силовой части гидропривода, имеет разрыв по первым производным. Во всех остальных точках расходно-перепадной характеристики коэффициенты Кдх и Кдр определяются формулами:
Рис. 5.2. Нелинейность расходной характеристики золотникового распределителя
|
Д<Ээ |
|
Рп “ Рсл ~ Рк О хз О |
|
= *1 |
|
КЯх = |
|
Дх3 ДС}з |
|
Р нО хзО |
|
К*х |
|
ЗО |
|
«Яр = |
|
Дхя |
|
2 /2(рп - Рсл ~ Рн О ж3 о) |
|
Р нО *зО |
 |
|
|
|
У реальных золотниковых устройств вследствие утечек и перетечек жидкости по зазорам функция (5.18) изменяется так, что разрывы по первым производным сглаживаются. Это позволяет в окрестности точки рК = 0, (2з = 0 вычислять коэффициенты по формулам (5.19) и (5.20), принимая в них рН0 = 0, а значение ж3о выбирать равным промежуточному значению между Х3 = 0 И Х3 = Жзщах-
Все рассмотренные выше допущения позволяют составить линейную математическую модель силовой части гидропривода с дроссельным регулированием. Эту модель можно еще несколько упростить, если связь выходного звена с телом массой га принять абсолютно жесткой. Тогда ушт = ут, а массы гап и га можно просуммировать, не учитывая при этом массу гидроцилиндра. При перечисленных дополнительных допущениях уравнения, описывающие в линейном приближении динамические процессы в силовой части гидропривода с дроссельным регулированием, сведем в следующую систему:
|
<а |
|
Л |
|
^0 + Уа &Ръ с Ушт с Уп _ п ~~г, Г Т. г - Эп ~77 — Чз'у |
|
2 В, |
|
<12у] |
|
Га- |
|
Шт. <1ушт _ I ^тр I СнУшТ — ^ПУН) |
|
<й2 |
|
|
|
Му дифференциальному уравнению
|
-+ |
![]() ГаУо <$ушт *^п (К<Эрт кТрУ() ^ <Рушт
ГаУо <$ушт *^п (К<Эрт кТрУ() ^ <Рушт
2Е11ЗпКЯх 6ХЗ ч - Кдх 52 + 2£ц52У <И2
|
^(1+ |
|
Ушт — (5.24) |
|
+ |
|
+ |
|
Я |
|
УрСн К<2рктр (1ушт Кдрсн |
|
2£ц5„2 |
|
- + |
![]()
Где Еи = ---------------- ту - .
V 9 Я 1 _1_ 1£ _1_
У<) У0Соп
Обычно величины, которые являются слагаемыми коэффициента при йушт/й1^ малы по сравнению с единицей. Исключив эти величины из уравнения (5.24) и преобразовав его по Лапласу при нулевых начальных условиях, получим
Тгб(Тцб2 + 2£цТцЗ + 1)ушт(5) — ®з(^) — ^нУшт(5)) (5.25)
Где
Тг = - I5-; (5.26)
Г"=У5 (5'27)
У0
^ _ 0,5А? тр + КдргпЕц/Уо /к
У^ТТЬСц
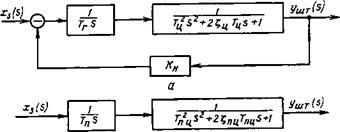
Согласно формулам (5.25) - (5.30), на основании рассмотренных в гл. 4 методов построена изображенная на рис. 5.3, а структурная схема. Из рисунка ясно, что линейную математическую модель силовой части гидропривода с дроссельным регулированием можно представить последовательно соединенными интегрирующим и колебательным (при Сц < 1) или апериодическим (при Сц > 1) второго порядка звеньями, охваченными отрицательной обратной связью с пропорциональным звеном. Каждое из указанных звеньев учитывает определенные физические процессы, возникающие в гидроприводе при динамических режимах его работы.
Интегрирующее звено с постоянной времени Тг описывает процесс непрерывного поступления жидкости в одну полость гидроцилиндра и вытеснения жидкости из другой полости при движении поршня гидроцилиндра. Значение Тт зависит от
|
5 Рис. 5.3. Структурные схемы силовых частей гидропривода с дроссельным регулированием (а) и пневмопривода (б) |
Рабочей площади 5П поршня гидроцилиндра и коэффициента Кдх преобразования перемещения золотника в расход жидкости через окна, открываемые кромками золотника. Чем меньше эта постоянная времени, тем больше скорость движения выходного звена гидропривода. Наличие колебательного или апериодического звена второго порядка вызвано сжимаемостью жидкости в гидроцилиндре и присоединенной к его штоку массой га. Находящаяся в гидроцилиндре жидкость играет роль пружины с жесткостью Сц, значительно превышающей жесткость сн пружины, имитирующей позиционную нагрузку на выходное звено гидропривода. Значение постоянной времени Тц = 1/и;оц, где ыоц — собственная частота колебаний массы га при среднем положении поршня гидроцилиндра. Демпфирование колебаний массы га создает сила вязкого трения в нагрузке на выходное звено и пропускная способность окон золотника. Первый фактор учитывается в коэффициенте Сц относительного демпфирования величиной А? тр, второй — величиной На первый взгляд, несколько неожиданно в структурной схеме показана обратная связь, которая отсутствует в конструкции силовой части гидропривода (см. рис. 5.1). Эта обратная связь означает, что величина уШТ влияет на расход жидкости, как бы изменяя величину х3. В действительности, расход жидкости изменяется вследствие увеличения и уменьшения давления в полостях гидроцилиндра при движении его поршня. Обратная связь, не предусмотренная конструкцией устройства, а возникающая вследствие внутренних физических процессов, может быть названа собственной или внутренней обратной связью.