Механика гидро - и пневмоприводов

Простейшие звенья структурных схем

Вид структурной схемы зависит от вида составляющих ее звеньев и от того, как эти звенья соединены между собой. Чтобы обеспечить общность расчетов различных по своему на­значению систем, в теории управления применяют так называ­емые типовые звенья, которые можно представить одинаковы­ми передаточными функциями независимо от природы процес­сов, протекающих в реальных устройствах. Такими звеньями являются: пропорциональное, интегрирующее, дифференциру­ющее, апериодическое и форсирующее первого порядка, а так­же апериодическое, колебательное и форсирующее второго по­рядка. Первые три из перечисленных звеньев имеют наиболее простые передаточные функции, с помощью которых можно получить передаточные функции остальных типовых звеньев при описании процессов в сосредоточенных параметрах. Если необходимо учитывать распределенные параметры, то процес­сы приходится описывать уравнениями в частных производ­ных, которым соответствуют трансцендентные передаточные функции. В некоторых случаях системы с распределенными параметрами можно преобразовать в системы со звеньями чи­стого запаздывания. Оба последних типа звена являются осо­быми динамическими звеньями.

Пропорциональное звено передает сигналы с постоянным соотношением их значений без смещения по времени. Зависи­мость выходного сигнала у от входного и для пропорциональ­ного звена определяется уравнением

У = Ки, (4.62)

Где К — коэффициент усиления, если входной и выходной сиг­налы являются безразмерными или величинами одной размер­ности; в других случаях этот коэффициент точее называть коэффициентом передачи или коэффициентом преобразования сигналов.

Значения коэффициента К находят по статическим харак­теристикам устройства или по передаточной функции (4.48), принимая 5 = 0.

Примерами устройств, которые по своим свойствам близ­ки к пропорциональному звену, могут служить рычажные и

Зубчатые механизмы при пренебрежимо малом влиянии инер­ции, упругих деформаций и трения в механизме. К пропорци­ональным звеньям относятся также малоинерционные датчи­ки, преобразующие неэлектрические величины (перемещения механических элементов, давления и расходы рабочих сред) в электрические (напряжения, токи).

Интегрирующее звено описывается дифференциальным уравнением

(4.63)

В котором Г — постоянный коэффициент, имеющий при оди­наковых размерностях входного и и выходного у сигналов раз­мерность времени, поэтому данный коэффициент называют по­стоянной времени.

Уравнение (4.63) можно также представить в виде

(4.64)

Где Ку = 1/Т — коэффициент усиления, определяемый отне­сенным к единичному значению входного сигнала значением скорости выходного сигнала. При изменении входного сигнала в виде единичной ступенчатой функции

И = 1(£)

Отклик (переходную функцию) интегрирующего звена нахо­дят, решая уравнения (4.63) или (4.64):

Или у(і) = Куі, (4.66)

Где произвольная постоянная равна нулю, так как принято, что при / = 0 значение у(0) = 0 (рис. 4.4, а).

Передаточная функция интегрирующего звена в соответ­ствии с уравнением (4.63) или (4.64) имеет вид

(4.67)

Подставив в передаточную функцию (4.67) 5 = получим амплитудно-фазовую частотную характеристику интегрирую­щего звена

Ф),
/Я
4(1).
1дЬ)
Р
6
Іди)
О
О	І
А
Г

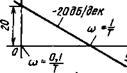
Рис. 4.4. Переходная (а), амплитудно-фазовая частотная (б), логарифмические амплитудная (в) и фазовая (г) характеристи­ки интегрирующего звена

Характеристика (4.68) при изменении и от 0 до +оо изображе­на на рис. 4.4, б. Эта характеристика показывает, что у инте­грирующего звена выходной сигнал при всех частотах отстает по фазе от входного сигнала на —7г/2. Амплитудная частотная характеристика звена определяется как модуль

(4.69)

Логарифмическую амплитудную характеристику интегриру­ющего звена строят с помощью уравнения

Ци>) = 201 %А(и>) = —20Ти = -201 %(и>/Ку). (4.70)

Уравнение (4.70) показывает, что ЛАХ является прямой, пе­ресекающей ось частот в точке, для которой и = 1/Т = Ку (рис. 4.4, в). Наклон прямой определяют изменением значе­ния Ь(и) при изменении и на декаду. Подставив в форму­лу (4.70) и = 0,1/Т и и = 1/Т, получим, что изменение Ь(и) равно —20 дБ. Следовательно, наклон ЛАХ составит —20 дБ/дек. Логарифмическая фазовая характеристика пока­зана на рис. 4.4, г прямой, параллельной оси частот, так как = —тг/2.

Уравнение (4.63) или (4.64) и характеристики интегриру­ющего звена отражают важное для многих физических процес­сов свойство накопления вещества, количества движения, элек­

Трического потенциала, что необходимо учитывать при мате­матическом моделировании различных устройств. Для приме­ра рассмотрим часто встречающееся в гидро - и пневмоприво­дах устройство (рис. 4.5), в котором поршень 1 рабочей средой, подводимой через клапан 2, перемещается в цилиндре 3. Если предположить, что поршень имеет нулевую массу га, а тре­ние между поршнем и цилиндром отсутствует, то давление Рц можно принять постоянным. При такой идеализации процес­са скорость поршня будет задана расходом ф рабочей среды, заполняющей увеличивающийся при движении поршня объем цилиндра:

Где 5П = тг^д/4.

Расход несжимаемой рабочей среды зависит от площади 5кл проходного сечения клапана, от его коэффициента /хкл рас­хода и разности давлений рп — Рц - Эту зависимость выражает формула

(4.72)

Где хкл — перемещение клапана; 6КЛ — ширина окон, откры­ваемых при перемещении клапана, 6Кл^кл = 5кл-

При постоянных значениях рп, Рц> Р расход ф изменяется только в зависимости от хкл. С учетом этих условий после подстановки ф из формулы (4.72) в уравнение (4.71) получим

(4.73)

Где Т = 5*п! |^кл&кл /2 (рп — рц)/р — постоянная времени рассмотренного механизма.

Дифференцирующее звено по своему математическому описанию является обратным по отношению к интегрирующе­му звену:

»-т£, (4 74)

Г — постоянная времени звена.

В соответствии с уравнением (4.74) передаточная функция дифференцирующего звена имеет вид

УУ(з) = Тз. (4.75)

Частотные характеристики можно найти, выполнив такие же действия, как при определении соответствующих характери­стик интегрирующего звена. Эти характеристики описывают уравнениями

МУЦи) = ]Тш (4.76)

Ци) = 20^Тш] (4.77)

Ч*ы) = +|. (4.78)

Амплитудно-фазовая частотная характеристика (4.76), ЛАХ (4.77) и ЛФХ (4.78) дифференцирующего звена приведены на рис. 4.6.

Вида (1.38) объемный расход ф среды, поступающей в замкну­тый объем УЬ, который заполнен той же средой, равен:

*-7% ^

Где В — локальный изотермический или адиабатический мо­дуль объемной упругости среды.

В электронных средствах управления гидро - и пневмопри­водами для корректирования динамических характеристик та­ких систем применяют элементы, близкие к дифференцирую­щим звеньям.