Оптоэлектроника

Электромагнитное описание нелинейной квадратичной оптической восприимчивости

Ангармоническое смещение электронов в нелинейном материале, подвергнутом возбуждению электромагнитной волны, приводит к излучению света с частотами 2а), 3со... Расчет оптического излучения из-за нелинейных членов-источников учи­тывается подобно случаю линейной оптики с использованием эффективного фор­мализма в виде уравнений Максвелла. Напомним уравнения Максвелла в отсут­ствие свободных зарядов (р= 0) и тока проводимости (} = 0):

У Е = 0 УВ = 0

УхЕ = -^-В УхВ = Ао|гО = Ао|-(£оЕ + Р)

Здесь Р есть вектор поляризации и сумма членов линейной поляризации Р,, опре­деляемых (12.8) или Р, = е0(п2о — 1) Е (при п = 1 + Хо а также нелинейной поляризации, определяемой, например (12.10). (Система уравнений (12.18) может быть записана в более компактном виде:

(12.19)

Уравнение распространения с членом источника

Для упрощения системы обозначений и концентрации нашего внимания на основных концепциях предположим, что система имеет одномерный характер и что все электромагнитные волны распространяются вдоль оси 01.

Как это показано на рис. 12.2, мы рассмотрим электромагнитные волны с час­тотами *у.(/ = 1,2 и 3 при соъ> со2> ю,), которые распространяются в нелинейном кристалле. Эти три волны могут быть описаны огибающими функциями, т. е. они могут быть записаны в виде:

£>.(*, /)= -[£,(0 еКш/г-Аг/г) + к. С. ] (12.20)

2

Напоминаем, что аппроксимация огибающей функции предполагает, что вари­ации амплитуды Е. (г) малы по сравнению с масштабом соответствующих длин волн А. = 2п/кп а именно:

С!£,. 7 62Е; /П1П

Аппроксимация огибающей функции

Более того, решения линейных уравнений Максвелла (без членов источника как в

(12.19) ) приводят к следующим дисперсионным соотношениям:

Щ = к,— (12.22)

П-

Эти три волны взаимодействуют в кристалле посредством нелинейной поляри­зации. Предположим, что вектор нелинейной поляризации ориентирован вдоль оси Оу, при этом мы будем рассматривать лишь его модуль Рп1. Нелинейный член ис­точника, в свою очередь, включает члены в Еа^, ОЕкоторые будут генерировать волны с круговой частотой со = со1+ со2. Аналогичным образом, члены источника в

0(или Ещ(1, 1)Ещ(ъ 0 будут генерировать волны с частотой со{ = со3 — со2 (или со2 = со3 — щ). Таким образом мы ожидаем проявление трех механизмов:

Со3 = сох + со2 суммарная частота

Сох = соъ — со2 разностная частота

Разностная частота

Например, нелинейный член источника, соответствующий механизму Б, полу­чается непосредственным обобщением (12.10):

0= -^[£2(г)*+ к. с.] (12.23)

На этой стадии рассмотрения важно отметить, что присутствие членов е+1<а/ или е~'ш; во временной зависимости будет сопровождаться соответственно членами Е.(1) или £Дг) в огибающей функции. Более того, понятно, что нет оснований приравнивать нелинейную восприимчивость х((0у~0>2) восприимчивости генерации второй гармо­ники Тем не менее, для того чтобы сохранять простоту обозначений, мы будем записывать восприимчивость в общем виде х2•

Теперь нам остается лишь подставить выражение для нелинейной поляризации (12.23) в качестве члена источника в уравнения Максвелла (12.19). Рассчитаем каж­дый из членов этих уравнений: Первый член может быть записан в виде:

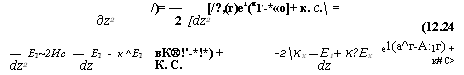Здесь мы использовали аппроксимацию огибающей функции (12.21). Таким обра­зом, уравнение распространения (12.19) может быть записано в виде:

2кх —Ех + к? Ех dz

£

—+ к. С.

2

Поскольку ф1 =к1с/п1 и со = со3 — со2, это уравнение может быть упрощено и записано более компактно в виде:

С1 '1 dz		+ К. С.]
+ к. с.	(12.26)

Теперь мы уже можем учесть изменение комплексной амплитуды Е1(г) в мате­риале (в функции эволюции амплитуд двух волн источника Е2Ц) и (г)),описывающей механизм генерации разностной частоты со{ = со3~ со2. Очевид­но, что два других механизма соъ = со{ + со2 и (о2 = сог — сох происходят одновременно с этим процессом. Амплитуды Е,(-£), Е2&) и Еъ(£) связаны друг с другом через следу­ющую систему дифференциальных уравнений:

Щ = щ - щ -%-Е, =

<1 2 щс

Е2 = -1^ Х2Е* Еге[Лк*

Й)3 = щ + сог <-> —Е} = -—^-Хг^Егй

Dz

Параметрические взаимодействия второго порядка

Мы оставляем читателю возможность самостоятельного вывода двух последних уравнений в (12.27). Отметим, что добавляемые частоты +со. приводят к члену Е. в

(12.27) , тогда как вычитаемые частоты — со1 дают члены Е* с правой стороны урав­нения. А к есть рассогласование фаз, определяемое как:

(12.28)

Рассогласование фаз