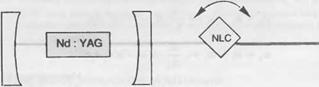Оптическая генерация второй гармоники
Сейчас мы опишем специфический случай, когда со = сох = со2 и со3 = 2со. Эта ситуация соответствует оптической генерации второй гармоники. Б этом случае уравнение
(12.27) Приобретает вид:
|
-1Д kz |
|
-ХгЕгшЕшй |
|
AkL |
|
Е2ЛЙ = — XiElLwic П2о)С |
|
В общем случае, нас более интересует оптическая мощность, преобразованная |
|
В излучение второй гармоники, связанной с амплитудой Е соотношением: |
|
= 2- |
|
2о) Р. |
|
1 |
|
(12.32) |
|
Л.= |
|
2 Zn |
|
Здесь Z0 — вакуумный импеданс = (/.1ь/е0)'п = 377 Ом). В этом случае эффективность преобразования второй гармоники есть: |
|
(12.29) |
|
О) |
|
2'iAkz |
|
Рис. 12.3. Природа возникновения разности фаз между полем нелинейной поляризации Р(2со) и полем второй гармоники Е(2со). |
|
-5—^2«, = ^ п2„с В этих уравнениях видно новое обозначение для Е. В основе появления члена А к СО Лежит то, что поле источника Р2ш синхронно с полем Еш (которое его и генерирует), которое имеет скорость распространения, определяемую с/пш, в то время как поле Е1(о обладает своей скоростью распространения в соответствии с п2а) (смотрите рис. 12.3). На время предположим, что эффективность нелинейного преобразования мала и соответственно Ею(£) остается практически постоянной по объему взаимодействия, т. е. что Еа(1) = Е0. Полный расчет приводится в дополнении 12.В. Второе дифференциальное уравнение в (12.29) может быть легко проинтегрировано вдоль траектории взаимодействия (на длине нелинейного кристалла от 0 до Ь), что позволяет найти: |
|
-1 |
|
(12.30) |
|
Мы можем применить метод, использованный ранее в (1.77) для нестационарных возмущений, который включает в себя умножение числителя и знаменателя в (12.30) на е-1АА:1/2, что приводит к: |
 |
|
|
|
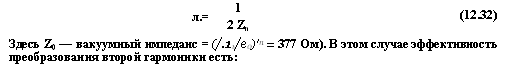 |
|
|
|
|
|
|
|
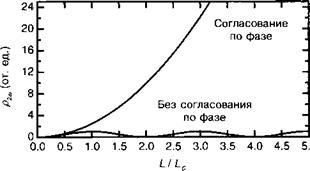
Рис. 12.4. Изменение мощности сигнала второй гармоники Р2о} в функции расстояния распространения в нелинейной среде для согласованных и несогласованных по фазе случаев. |
Ц = т?—2 ч (12.34)
Длина фазового рассогласования
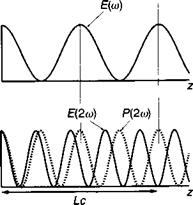
Здесь Л0 есть длина фундаментальной электромагнитной волны в вакууме. Этот параметр Ьс в литературе некорректно называется длиной когерентности. Очевидно, что существование такой длины максимального преобразования связано с естественной дисперсией, имеющей место в нелинейном материале (исключение составляют резонансы материала, где дисперсия может быть аномальной), где п(2со) > п(со). Анализ (12.29) и (12.30) позволяет понять осцилляционную природу энергетического обмена между фундаментальной волной и ее второй гармоникой. Можно показать, что при
I < Ьс работа, совершаемая волной с частотой со над диполями с частотой 2со, положительна тогда, когда при Ьс< I <2Ьс имеет место обратная ситуация.
Пример-------------------------------------------------------------------------------------------------------------
Мы хотим использовать кристалл ваА* для преобразования пучка излучения с длиной волны 10,6 мкм в излучение с длиной волны 5,3 мкм. ваА* — это материал с очень сильной нелинейной восприимчивостью на длине волны 10,6 мкм. Предположим, что в этой экспериментальной конфигурации ~ Ю0 пм ^ • При эт°м, другие необходимые нам константы составляют:
П (5,3 мкм) — п (10,6 мкм) = 2,5 х 10-2 (смотрите соотношение Зеллмайера в дополнении 7.Б).
Я(5,3 мкм) ~ я(10,6 мкм) ~ 3.
В этом случае оптимальная длина для достижения максимальной эффективности преобразования дается соотношением = 10,6 мкм/(4 х 2,5 х 10-2) = 10,6 мкм. При этом достижимая эффективность составляет:
|
Ш-Ои |
![]()
|
Р = 2х |
![]() : [1,8 х 10|4с~' х 10'4м х 8,85х 1<Г'2 Фм'']х [кГ10 мВ']^
: [1,8 х 10|4с~' х 10'4м х 8,85х 1<Г'2 Фм'']х [кГ10 мВ']^
Т. е.:
Р,
^ = 10-"^(Вт см 2)
Р(и
В предположении Ра = 1 МВт см-2 эффективность преобразования составляет всего 10'5, что является разочаровывающим обстоятельством. Причиной такой малой эффективности является рассогласование фаз, ограничивающее эффективную дину взаимодействия на уровне 100 мкм.
|
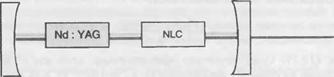
Рисунок 12.5 иллюстрирует различные экспериментальные конфигурации для реализации удвоения оптической частоты: а) кристалл удвоения частоты может быть помещен за пределами лазерного резонатора, б) для использования преимуществ оптической обратной связи кристалл удвоения частоты может быть располагаться и внутри оптического резонатора (смотрите дополнение 12.Д), в) и, наконец, очень компактная (микрокристальная) конфигурация может быть реализована за счет нанесения зеркал на обе стороны расположенного рядом YAG и слои кристалла удвоения частоты, так как в этом случае для накачки структуры может быть использован лазерный диод.
|
|
|
Рис. 12.5. Различные конфигурации для генерации второй гармоники на длине волны 530 нм с использованием лазера на основе Nd: YAG на длину волны 1,06 мкм. Нелинейный кристалл (NLC), помещенный вне оптического резонатора и ориентированный таким образом, чтобы обеспечивать угловое согласование фаз (л), внутрирезонаторное преобразование с использованием NLC, ориентированное таким образом, чтобы обеспечивать угловое согласование фаз (б), микрокристальное преобразование с использованием зеркал, нанесенных на обе поверхности слоев Nd: YAG и NLC.