ЭЛЕКТРОННЫЙ ЦИКЛОТРОННЫЙ РЕЗОНАНС ЭЛЕКТРОМАГНИТНЫХ КОЛЕБАНИЙ, РАСПРОСТРАНЯЮЩИХСЯ ПОПЕРЕК НЕОДНОРОДНОГО МАГНИТНОГО ПОЛЯ
А. В. ЗВОНКОВ, А. В. ТИМОФЕЕВ Введение
Для электронных циклотронных колебаний, т. е. электромагнитных колебаний с частотой <о, примерно равной электронной циклотронной ю,, характерно, что их свойства существенно зависят от угла 0 между магнитным полем Н0 и волновым вектором колебаний к. Если магнитное поле неоднородно, то возникает также зависимость от угла ^ между Н0 и УН0.
Электронные циклотронные колебания в неоднородном магнитном поле при рассматривались в [4]. Колебания, распространяющие
Ся под произвольным (однако отличным от л/2) углом 0 к Н0, были проанализированы в работах [2 3], причем в [2] предполагалось, что ф=0, и в [3], что
В настоящей работе рассматриваются колебания, распространяющиеся поперек магнитного поля (0*=л/2). Угол 0=л/2 особенно удобен для введения ВЧ-мощности в тороидальные системы, а также для наблюдения спонтанного излучения из таких систем. Поэтому анализу случая 0=я/2 было посвящено большое число работ (см., например, [4~12]). При учете неоднородности магнитного поля, если такое производилось, угол ф принимался равным я/2, что соответствует геометрии магнитного поля тороидальных систем. Отметим, что влияние неоднородности магнитного ПОЛЯ На резонансное взаимодействие циклотронных колебаний с электронами, как правило, учитывалось параметрически. А именно, колебания характеризовались коэффициентом поглощения, полученным для случая однородного магнитного поля, в котором величина поля считалась медленно меняющимся параметром.
Естественно, что вопрос об отражении колебаний от резонансной зоны, где ©«©.(г), выходит за рамки такого подхода. Этот вопрос для случая 0=г|)=я/2 был поставлен в работе [*], в которой найдено, что коэффициент отражения обыкновенных колебаний, падающих на резонансную область со стороны большего поля, равен нулю. Однако утверждалось, что обыкновенные колебания, распространяющиеся в противоположном направлении, частично отражаются, причем если выполнено условие Г>1, То отражение оказывается практически полным. Здесь Г=(я/4)д(1— —ДУ'*(Ь(д1с) (и./с)*, £=(й)р./й).У , юр* — плазменная электронная частота, Ь — характерный масштаб изменения магнитного поля, Ив*=(Тв/тв)'к. Из результата, полученного в [•], следует, в частности, что при нагреве плазмы в токамаке ВЧ-мощность нельзя вводить с внешней стороны тора.
Недостатком работы [в] является игнорирование релятивистской зависимости циклотронной частоты от энергии электронов. Между тем при распространении поперек магнитного поля (0=я/2) именно эффекты, обусловленные такой зависимостью, и определяют структуру колебаний в
области резонансного взаимодействия. Нами показано, что влияние релятивизма приводит к значительному снижению коэффициента отражения. В результате при любых значениях Г коэффициент отражения оказывается существенно меньше коэффициента поглощения.
В настоящей работе также определен коэффициент поглощения необыкновенных колебаний при прохождении через зону резонансного взаимодействия. Из-за учета релятивизма он отличается от полученного в [9]. Что касается отражения необыкновенных колебаний, то оно, как и в случае обыкновенных, оказывается несущественным.
1. Обыкновенные колебания
А. Адиабатическое волновое уравнение
Обыкновенные колебания, распространяющиеся поперек магнитного поля, описываются следующим волновым уравнением:
^-(i+*¥{х))17е‘+(т) (D
Здесь использована декартова система координат, ось ОХ которой направлена вдоль Vtf0, ось OZ — вдоль Н0; плазма предполагается однородной; 7(x)«=‘/tfv,(g(x)); G(x)={c/v. y(ь>-Ш.(х))/ш; ш#(х)=еЯ0(х)/т, с,
Те — масса покоя электрона; F,(g) = ^ (—g)p(s — P—2)l/(s—l)!+
Р —О
+*л(—g)e“W((—g)v,)/(s—1)!; W — интеграл вероятности от комплексного аргумента. В дальнейшем нас будут интересовать явления, происходящие в окрестности «резонансной» точки я,((о=(о.(:гв)). В этой области можно принять, что магнитное поле меняется по линейному закону Н0(х) = =Я0(1—X/L). Поскольку считается, что D(oJdxx~x,<0 и точка Х, является точкой ветвления функции V(x), последняя, в соответствии с правилом обхода Ландау, однозначно определена лишь в верхней полуплоскости комплексного переменного X.
В (1) учтены эффекты, обусловленные конечностью ларморовского радиуса электронов и зависимостью электронной циклотронной частоты от энергии. При выводе (1) использовались предположения (уе/с)2<1 и | (uj(d)d/dx <1, распределение электронов по скоростям предполагалось максвелловским с температурой Тв^твивг. В случае однородного поля уравнение (1) принимает хорошо известный вид:
|
Giz, |
Где Ггх определено в [4*5].
На достаточно больших расстояниях от резонансной точки Х„ в области, где выполняется условие I (О—й).(х) | >й) (уе/с)2, (1) можно заменить следующим приближенным уравнением:
Т~(1+49—^Тг(—)*)гЕ' + (—)г и-з)5’“0- (2>
Дх 2 со—со» (х) с / Iдх с /
В последнее уравнение не включены эффекты резонансного циклотронного взаимодействия, а неоднородность магнитного поля учитывается в нем
Параметрически. Подобные волновые уравнения принято называть адиаба -
Г
Р
Тнческими. Заменяя Ег(х) на ДлЕг(х) И смещая начало отсчета
иа х,—/д/2, приводим уравнение (2) к виду
+ <з,
Где 1=Ь(ив/с)г. Посредством замены х-»-2«:((о/с) (1—д)[59]'[60] уравнение (3) приводится к уравнению Уиттекера.
Для определения коэффициентов поглощения и отражения колебаний необходимо установить правила соответствия между асимптотиками решений, заданными по разные стороны от начала координат (резонансной области). Такие правила наиболее просто найти, обходя начало координат на достаточно большом расстоянии в верхней полуплоскости комплексного переменного Х. Используя свойства решений уравнения Уиттекера [[61]], находим, что колебания, падаюшие-^на резонансную область со стороны большего магнитного поля (х<0), проходят через нее без отражения, а их коэффициент поглощения по мощности равен 1
TOC o "1-5" h z Т1=1-ехр(-2Г). (4)
Велнчпна Г была определена во Введении. Колебания, падающие со стороны меньшего поля (д:>0), отражаются с коэффициентом
5—(1—ехр (—2Г)):. (5)
Коэффициент поглощения таких колебаний отличается от (4):
Л=ехр(-2Г)(1-ехр(-2Г)). (6)
Отметим, что коэффициент прохождения £=1—г]—^ не зависит от направления распространения колебаний
£=ехр (—2Г).. (7)
Выражения (4) —(6) были получены в [•], они имеют тот же вид, что и найденные ранее в [’], отличаясь от последних лишь значением показателя экспоненты Г. Напомним, что в [*] рассматривались необыкновенные колебания при 0=-ф=О.
Б. Квазнклассическое приближение
Предположим, что параметр квазиклассичности х=(/ю/с) (1—д)' определяемый как отношение характерного пространственного масштаба функции V (х) — I к характерной длине волны колебаний —А:”"1, значительно превышает единицу. Здесь К-'(со/с) (1—д)7*. В этом случае пространственная зависимость колебаний, описываемая (1), всюду имеет квазикласси - ческий вид, а коэффициент отражения должен быть экспоненциально мал по параметру* х. Этот результат находится в явном противоречии с полученным в [•] (см. также предыдущий раздел), где на основании анализа адиабатического волнового уравнения, аналогичного (2), утверждалось, что при выполнении условия Г=ядх/4>1 колебания, распространяющиеся со стороны меньшего магнитного поля, практически полностью отражаются.
Однако адиабатическое волновое уравнение, строго говоря, справедливо лишь в том случае, если резонансное условие для всех электронов выполняется в одной точке. При распространении поперек магнитного поля к размытию резонансной зоны приводит релятивистская зависимость электронной циклотронной частоты от энергии, что не учитывалось в [9].
Отметим, что если колебания распространяются под острым углом к магнитному полю, то к размытию резонансной зоны приводит также и эффект Доплера. Анализируя этот случай, авторы работы [9], так же как и мы, пришли к выводу, что если размер резонансной зоны достаточно велик, то - коэффициент отражения должен быть экспоненциально мал.
Выясним, почему использование адиабатического волнового уравнения: привело к ошибке. Для этого вспомним, что в квазиклассическом приближении возникновение отраженной волны выглядит как явление Стокса (изменение I асимптотического представления решения
| на линиях мнимой фазы — линиях Стокса)
|
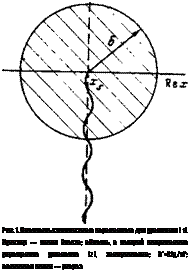
Рис. 1. Плоскость комплексного аеременного для уравнения (1). Пунктир — линия Стокса; область, в которой неприменимо упрощенное уравнение (2), заштрихована; 3*=£(у,/с)2; волнистая линия — разрез |
 (см., например, [|4]). В данном случае асимптотика решений уравнения (2) имеет вид
(см., например, [|4]). В данном случае асимптотика решений уравнения (2) имеет вид
Ег(х) «я±|Г/я exp (±Ikx), (8)
А линия Стокса направлена вертикально вверх (пунктир на рис. 1). На этом рисунке заштрихована область, в которой неприменимо упрощенное адиабатическое волновое уравнение (2).
Из (8) следует, что решение, описывающее волну, бегущую влево, на линии Стокса экспоненциально нарастает. К нему„ вообще говоря, может быть добавлено спадающее решение, соответствующее волне, бегущей направо, т. е. отраженной. Амплитуда отраженной волны может быть определена только с помощью точного волнового уравнения (1). Действительно, в адиабатическом уравнении (2) учтен лишь, первый член асимптотического разложения функции Fi/X(G) по большому аргументу. Любой из следующих членов, будучи помножен на экспоненциально растущую часть решения, превысит экспоненциально спадающую часть, которая соответствует отраженной волне. Поэтому не удивительно, что коэффициент отражения был определен с помощью (2) неправильно.
В то же время уравнение (2) пригодно для определения коэффициента прохождения колебаний £. В самом деле, при переходе с левой действительной полуоси на правую argx уменьшается на л. Поэтому решение (8), описывающее волну, бегущую влево, увеличивает свою амплитуду при таком переходе на ехр(Г), и, следовательно, коэффициент прохождения £ совпадает с (7).
Совершенно аналогично доказывается, что коэффициент прохождения колебаний, бегущих в противоположную сторону, также равен (7). Отметим, что в этом случае решение адиабатического волнового уравнения (8) позволяет установить и отсутствие отраженной волны. Действительно, интересующее нас решение спадает в верхней полуплоскости, и, следовательно, при переходе через линию Стокса его асимптотика не меняется.
В. Метод последовательных приближений
Если коэффициенты поглощения и отражения малы, их можно найти аналитически, используя метод последовательных приближений. При выполнении условия Г<1 решение уравнения (1) всюду, в том числе и в резонансной зоне, будет слабо отличаться от плоской волны £*0)(х)*= «ехр (—Ikx). (Мы рассматриваем более интересное решение, описываю-
Щее волну, падающую со стороны меньшего магнитного поля.) Поправка к решению, учитывающая влияние резонансного взаимодействия, имеет вид
I *
(*) = - — gj Ac'(exp(г*(*'-*))-
- TOC o "1-5" h z exp(-ik(x'—x)))~~r V(x')Exp(-ikx ). (9)
OX
Из (9) находим, что при единичной амплитуде прошедшей волны амплитуды падающей и отраженной даются выражениями:
Л„..=1+у*д $Dx’V(X'), (Ю)
Оо
00
Лотр = -^-А:д| Dx' V(X')Exv(-2Ikx'). (11)
— оо
При вычислении интегралов в (10) —(11) выражение для V (х') удобно записать, используя интегральное представление Fyt(G(X')) (см. [5]):
О
V(x') = —L— j Dt(i+it)-v*exp(~ig(x')t),
— 00
Где при линейном изменении магнитного поля с координатой G(X') — = (C/Ve)2(X'—Xa)/L. В (10) поменяем порядок интегрирования. Интеграл
•
По Х' дает б(T). Тогда, полагая JЛ6(0/(0"*/(0)/2, получим: Лпая=
-оо
=1+Г. Аналогичным образом вычисляя интегралы в (11), получим
4отр=2Г(1-2;х)-т/«ехр (-2Ikx,).
Эти выражения дают коэффициент поглощения по мощности, совпадающей с (6): Г~ |<4пад|2— |-4отр|*—1»2Г<1. Для коэффициента отражения имеем:
£«|4отр|2=4Г2(1+4х2)-7/*. (12)
При х<1 этот результат совпадает* с (5). Это вполне понятно, так как длинноволновые колебания «не чувствуют» тонкой структуры резонансной зоны, где проявляется различие между точным волновым уравнением и адиабатическим. С другой стороны, коэффициент отражения коротковолновых колебаний (х»1) значительно меньше, чем следует из (5). Это подтверждает вывод предыдущего раздела о непригодности адиабатического волнового уравнения для описания коротковолновых колебаний.
Для колебаний, падающих со стороны большего магнитного поля, аналогичные вычисления дают т]«2Г, |=0.
Заметим, что коэффициент отражения коротковолновых колебании (х»1) можно найти при произвольных значениях Q, не накладывая условия Г<1, которое использовалось выше. Отражение таких колебаний обусловлено главным образом наличием точки ветвления Х, у функции V(X), Причем поскольку особенность функции V(х) в точке Х, является довольно «слабой» (V’(z)x_*f«C,1+C,2(x—Х, У/г), то коэффициент отражения может быть определен по методу последовательных приближений. Вычисления дают в этом случае
1~я*2-у х“5(1+д/5),/». (13)
Нетрудно видеть, что при 1, х>1 выражения (12) и (13) совпадают.
Аналитически нам удалось рассмотреть колебания, для которых выполняется одно из двух условий: х>1 (коротковолновые) или Г<1. Расчеты, выполненные с помощью ЭВМ, позволили исследовать и область значений Г^1 при х<1. В этой области длина волны колебаний по порядку величины равна размеру резонансной зоны и отражение обусловлено «плавной» неоднородностью функции У(х). При переходе к большим значениям
|
|
|
*(*тЮ)'Ог |
Рис. 2 Рис. 3
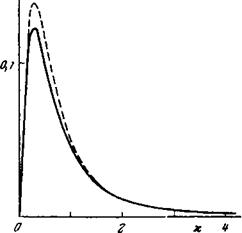
Рис. 2. Зависимость коэффициента отражения по амплитуде % для обыкновенных колебаний, падающих со стороны меньшего магнитного поля, от параметра квазиклассичности х. Пунктир — коэффициент отражения, рассчитанный по (12)
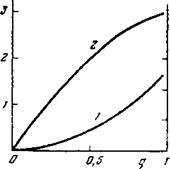
Рис. 3. Зависимость максимального коэффициента отражения £тах=£ (*т*х) (кривая 1) и коэффициента поглощения т) (х«.,) (кривая 2) от Д
Х (х>1) область отражения стягивается к точке которая является особой для функции V (х).
Нами решалась задача Коши для уравнения, полученного интегрированием (1):
+ (-^-)г (1-*)*-0, (14)
*
Где Р — J <1хЕг(х). Для ^ ставились «начальные» условия, соответствующие волне, прошедшей через резонансную зону. Путем численного интегрирования уравнения находилось решение перед резонансной зоной. Из него выделялись падающая и отраженная волны, и по их амплитудам определялись коэффициент прохождения колебаний 5 и коэффициент отражения |. Интегрирование проводилось по схеме Руйге — Кутта с автоматическим выбором шага.
Как следует из предыдущего рассмотрения, коэффициент прохождения дается формулой (7) при произвольных значениях параметров д и х и вне зависимости от направления распространения колебаний. Этот результат удобно использовать для контроля точности вычислений. Нами найдено, что рассчитанные значения коэффициента прохождения согласуются с определенными по формуле (7) с точностью не хуже, чем 10“
Результаты расчетов иллюстрируют рис. 2, 3. На рис. 2 представлена типичная зависимость коэффициента отражения колебаний, падающих
Со стороны меньшего магнитного поля, Ъ(Ъ=Аог»/А п*я | от параметра
Квазиклассичности х при фиксированном значении д (д=0,5). При значениях х<хта*(хтах~0,3) зависимость £ от х приближенно описывается формулой 6=2Г=ядх/2. При х>хтах коэффициент отражения падает с ростом х, как это и следует из предыдущего рассмотрения. Закон спада приближается с ростом х к определяемому (12), (13). Отметим, что хотя принятое нами значение д=0,5 не слишком мало, рассчитанная зависимость |(х) во всей области изменения х близка к определяемой из (12) (см. рис. 2). Напомним, что выражение (12) было получено в предположении д<1.
Что касается колебаний, падающих на резонансную область со стороны большего поля, то для них в пределах точности вычислений коэффициент отражения оказывается равным нулю.
При изменении Д Положение максимума кривой £(х) меняется слабо, так что всегда Хтах^ОД Величина максимума растет с увеличением Д. На рис. 3 показана зависимость коэффициента отражения в максимуме 6тах= -6(х них) И Коэффициента ПОГЛОЩеНИЯ Т| (Хцщх) ОТ ВеЛИЧИНЫ д. При Х'^Хтах
Для приближенного определения ^ и т) можно использовать формулы (5),
(6) , откуда получаем 5«4Г[62], т]«2Г и, следовательно, 5<т]. При х>хтах коэффициент отражения падает, а коэффициент поглощения с хорошей точностью дается формулой т^=1—£—£«1—ехр (—2Г). Значит, максимум отношения £/т] достигается вблизи Хщ** и, как следует из рис. 3, он не превышает 7в.
Таким образом, коэффициент отражения колебаний, распространяющихся со стороны меньшего магнитного поля, значительно меньше коэффициента поглощения при произвольных значениях х. Что касается колебаний, распространяющихся в противоположном направлении, то они проходят через резонансную область без отражения (см. выше). Учитывая соотношение 14=1—£ и (7), находим, что коэффициент поглощения в первом случае приближенно, а во втором точно дается формулой (4).
2. Необыкновенные колебания
Как известно, необыкновенные колебания, распространяющиеся поперек магнитного поля, при ©«со, взаимодействуют с электронами гораздо слабее обыкновенных. Параметр Г« (см. ниже), характеризующий интенсивность резонансного взаимодействия, практически всегда оказывается значительно меньше единицы (Г«~(1>«/с)2Г). Выше мы видели, что при Г«1 влияние резонансного взаимодействия на распространение колебаний может быть учтено по методу последовательных приближений. В настоящем разделе мы также будем использовать этот метод. Он позволяет определить коэффициенты поглощения и отражения колебаний с помощью упрощенного адиабатического волнового уравнения.
Волновый вектор необыкновенных колебаний, как известно, определяется дисперсионным уравнением
Кхг ** (е,*+е**в/е«).
Компоненты тензора е* при к-!_Н0 были определены в [[63]* [64]]. Возьмем их. асимптотические значения при | со—ю, | (и,/с)2. Заменим в дисперсионном
<1
Уравнении К на —*—. Полученный дифференциальный оператор следует
В соответствии с [[65]] применить к компоненте электрического поля колебаний, перпендикулярной основному магнитному полю и вращающейся в ионную сторону Е+=ЕХЛ-1ЕУ. В результате получаем следующее адиаба-
^г£* + (т)'(2-,,"+ш’,,£*-0' <*5>
Г., -4(I)' (, +(2-г)-,_Л_}.
2Q к © 2 с / ы)—(Oe(x) J
Уравнение (15) пригодно при не слишком низкой плотности плазмы, когда выполняется условие (Ue/c)z<.q. Оно отличается от использованного в [•] учетом эффектов, обусловленных релятивистской зависимостью электронной циклотронной частоты от энергии.
Рассмотрим сначала колебания, падающие со стороны меньшего магнитного поля. Учитывая в (15) член, пропорциональный U(x), как малую поправку, при единичной амплитуде прошедшей волны для Лпад и Лотр
Получаем выражения (10), (11) с заменой У(х) на------------- U(x). При вы-
9.
Числении Лпад деформируем контур интегрирования в (10) таким образом, чтобы он имел вид полуокружности бесконечного радиуса, расположенной в верхней полуплоскости. При этом получаем Лаад—1+Ге*, что дает коэффициент поглощения по мощности, равный я«Л|ад —1«2Г«, где Тех= = (я/8д) (2—Q)’L‘(Ve/C)K(UL/C) (1+(2—Q)*). Чтобы найти Лотр, контур интегрирования в (11) также удобно сместить в верхнюю полуплоскость, замкнув его полуокружностью бесконечного радиуса, лежащей в нижней полуплоскости. Это возможно в силу того, что экспонента ехр (—2Ikx) Спадает при 1тх<0. Вычисляя вычет в точке я*=0, получаем Л01р=2Г«е, и, следовательно, £«4Г«Л Отметим, что это выражение для £ справедливо лишь при x«=ss((щL/c) (ve/c)2(2—Т. е. для длинноволновых колебаний. В обратном предельном случае х.*>1 учет тонкой структуры резонансной области должен привести к спаданию по закону ~х«Г3 (ср. с (12), (13)).
Для колебаний, распространяющихся в противоположном направлении,, при произвольных значениях х,* получим я«2Г«, 5=0.
В заключение остановимся на условиях применимости результатов, полученных в настоящей работе. В ней считалось, что угол 0 между к и Н0 равен я/2. Однако полученные результаты справедливы и при 0^я/2, если выполнено условие я/2—0<у,/с. В том случае, когда отличен от я/2 угол Я между Н0 и УЯо, а колебания распространяются под некоторым углом ф к проекции V#o на плоскость, перпендикулярную Н0, в выражениях для коэффициентов 5, Tj, З, найденных нами, следует L заменить на L/cos ф sin Последнее утверждение справедливо при cos i|)<Ј<i)z;,3/c4.
Авторы выражают благодарность Г. Н. Чулкову за полезные обсуждения.
Институт атомной энергии Поступила в редакцию
Им. И. В. Курчатова 12 февраля 1980 г.