ПРАВИЛО ОБХОДА ЛАНДАУ В ПРОБЛЕМЕ ЦИКЛОТРОННОГО РЕЗОНАНСА В НЕОДНОРОДНОМ МАГНИТНОМ ПОЛЕ
ТИМОФЕЕВ А. В., ЧУЛКОВ Г. Н.
1. В неоднородном магнитном поле обмен энергией между электромагнитными колебаниями и заряженными частицами локализован в окрестности резонансной точки, где частота колебаний совпадает с циклотронной. Процессы, происходящие в этой области, столь сильно влияют на состояние частиц, что последствия резонансного циклотронного взаимодействия ощущаются на значительных расстояниях от резонансной точки (информация о резонансном взаимодействии переносится частицами вдоль магнитного поля вследствие их теплового движения). В результате связь электрического поля колебаний с вызываемыми им токами становится нелокальной и соответственно волновое уравнение интегральным. Это вполне естественно, так как обсуждаемая задача принадлежит к классу задач о распространении колебаний в неоднородной диспергирующей среде.
Решение интегрального уравнения представляет значительные трудности, однако обычно реальный интерес представляет не точный вид решения в окрестности резонансной точки, а значения коэффициента поглощения колебаний в резонансной области и коэффициента отражения от нее. В [1], где рассматривались колебания, распространяющиеся вдоль магнитного поля при 7Я0||Н0, было показано, что для вычисления коэффициентов поглощения и отражения колебаний можно применить упрощенный подход. А именно, использовать для тензора диэлектрической проницаемости выражение, полученное в однородном случае, когда’ тензор является довольно простым алгебраическим или дифференциальным, а не интегральным оператором, учитывая в нем зависимость магнитного поля от координат параметрически. Такое упрощение, строго говоря, законно лишь на достаточно больших расстояниях от резонансной точки. Поэтому для сшивки решений, задаваемых по разные стороны от нее, следует рассмотреть аналитическое продолжение волнового уравнения на плоскость комплексного переменного 5 (координата вдоль V#о) и обходить резонансную точку в комплексной плоскости в соответствии с правилом обхода Ландау.
В [2] возможность использования упрощенного подхода при К Н0 была подтверждена прямым решением интегрального уравнения в предположении, что коэффициент поглощения мал по сравнению с единицей. В настоящей работе показано, что такой подход можно использовать при произвольной величине коэффициента поглощения вне зависимости от направления векторов Н0, 7Я0 и к (волновой вектор)
Существенное упрощение тензора диэлектрической проницаемости при переходе к комплексным значениям координаты вполне понятно.
1 Наш анализ не охватывает случая УЯо-*-Н», когда возможность жсподьзованжя правила обхода Ландау очевидна.
5 Фважка плазмы, вып. 1 129
Действительно, если смещение с оси 1т $ =»0 происходит в соответствии с правилом обхода Ландау, то оно эквивалентно переходу к нарастающим колебаниям с инкрементом ч=о> Iт $/£. (Мы принимаем, что магнитное поле, а вместе с ним и электронная циклотронная частота, меняются по линейному закону шДз) =ш.0(1—$/£).) Рассматриваются электронные
Циклотронные колебания с ш=гсй)ео, зависящие от времени по закону
Ехр (—ш£)' Если амплитуда колебаний возрастает с инкрементом ч, то на состояние плазмы в данный момент времени влияют электрические поля, отдельные временным интервалом, не превышающим по порядку величины ч“1. Иными словами, в случае нарастающих колебаний фазовая
 Память частиц охватывает интервал времени порядка - р1. Если этот интервал окажется малым по сравнению с временем прохождения электрона через резонансную зону б£, то эффекты фазовой памяти станут несущественными и для тензора диэлектрической проницаемости можно будет использовать локальное выражение. Поскольку (см., например, [*■ *• 4]), то для соответствующего радиуса обхода бз поручаем выражение бз«(рЕЬ)ч здесь Ре — Средний ларморовский радиус электронов.
Память частиц охватывает интервал времени порядка - р1. Если этот интервал окажется малым по сравнению с временем прохождения электрона через резонансную зону б£, то эффекты фазовой памяти станут несущественными и для тензора диэлектрической проницаемости можно будет использовать локальное выражение. Поскольку (см., например, [*■ *• 4]), то для соответствующего радиуса обхода бз поручаем выражение бз«(рЕЬ)ч здесь Ре — Средний ларморовский радиус электронов.
К ухудшению фазовой памяти приводят и случайные воздействия — кулонов - ские соударения, немонохроматичность колебаний. В [2] было показано, что правило обхода Ландау можно использовать при наличии в плазме случайных воздействий достаточно высокой интенсивности. В настоящей работе предполагалось, что случайные воздействия отсутствуют. Естественно, что правило обхода Ландау остается справедливым и в промежуточном случае. Однако было бы неверным на этом основании считать, что правило обхода Ландау можно использовать при любых условиях и что поэтому обсуждаемая проблема вообще отсутствует. Действительно, в настоящей работе предполагается, что размеры системы неограниченно велики и поэтому каждый электрон проходит через резонансную зону лишь один раз. Полученные результаты можно использовать и для систем конечного размера, если в них фаза циклотронного вращения «сбивается» стохастически за одно прохождение электрона по системе. Между тем в [3] показано, что в ограниченных системах при отсутствии случайных воздействий правило обхода Ландау оказывается справедливым лишь, если амплитуда колебаний не слишком мала. Правило обхода Ландау нельзя использовать и в том случае, если резонансная точка приближается к экстремуму магнитного поля на расстояние Д 5где Ьх определяется соотношением #о(5)=#о(1=1:
±5*/^!*) (см. [4]). Напомним, что в настоящей работе предполагается линейный закон изменения магнитного поля. В силу малого размера резонансной зоны ~(рвЬ)4* такая аппроксимация в большинстве случаев является законной.
Наконец, отметим еще одно предположение, использованное нами. Мы считаем, что электроны в пределах резонансной зоны движутся вдоль магнитного поля равномерно. Если распределение электронов по энергиям в достаточной степени размыто, то для большинства электронов это предположение является вполне разумным. Однако оно заведомо нарушается для небольшой части электронов, останавливающихся в пределах
Резонансной зоны. В Приложении показано, что наличие ускорения не влияет на возможность использования правила обхода Ландау.
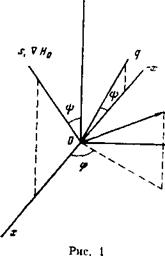
2. Рассмотрим электромагнитные колебания, распространяющиеся по плазме, помещенной в неоднородное магнитное поле. Введем декартову систему координат с осью ОZ, параллельной Н0, ось ОХ направим так, чтобы Vtfo находился в плоскости X0Z. В дальнейшем нам понадобится
Также вспомогательная система координат, повернутая на угол ij>=H0V#0 относительно оси О У (см. рис. 1).
Как отмечено выше, при учете эффектов пространственной дисперсии связь между электрическим полем колебаний и вызываемым им током является нелокальной и соответствующий оператор диэлектрической проницаемости интегральным. Так, найример, та часть я-компоненты плотности тока, которая вызывается z-компонентой электрического поля волны, имеет вид
/==УI <*3v/.(v)J Dk, Ex(k,)X
(1)
X (/п2(X)-2(1-cos 2Ф)()/п+1 (X)) | dxexp(-i<Ms, т)-шЖкг).
— оо
Это выражение получено стандартным методом интегрирования по траекториям. При его выводе электрическое поле представлено в виде
Ех(т, T) =Ex(S)Ex])(—I(Dt+Ikyy+Ikqq)
И для Ex(S) использовано разложение в интеграл Фурье:
£,(*) = (2л) J Dk. Ех(К,) exp {ik, s).
В (1) введены обозначения К^к, sin 1|>—Л, cos 1|>,
Kt=K, cos 1|>+&, sin |), cp=arctg (&„/&*), X=KxvJ(Oe,
Значок «перпендикулярно» отмечает величины, ортогональные к Н0:
Фп($, т) =Лпт+бт2, Ля=й)—mo.(s) — Ktuly 6=<oz;Icos $/2L,
Jn — функция Бесселя индекса П.
Используя одно из определений интеграла вероятности
TOC o "1-5" h z j Dx exp (-гд. т-.бт*) 4'W^N/2 W *> • (2)
— oo
Представляем (1) в виде
^ Dk. E.(k.)AnX
N™ — oo
X(Й)~'hWExp(-i0)t+&r). (3)
Здесь
A" = (w)
0
— 2 (1—cos 2ф) (X) /»+! (A.) J.
Функция распределения электронов по скоростям предполагается максвелловской.
|
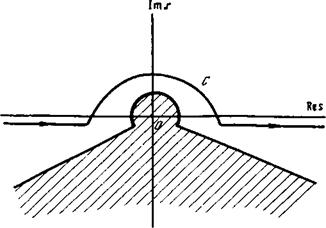
Рис. 2. Плоскость комплексного переменного S. Область, в которой необходимо учитывать влияние резонансного взаимодействия, заштрихована, С — контур обхода резонансной точки 5=0 в соответствии с правилом Ландау |
3. Как показано в [1—4], заряженные частицы эффективно обмениваются энергией с колебаниями в области, где выполняется условие |s|< <max(LЙ, z;*/<i); (Lvt cos ^/ю)'7*). Эту область и имеет смысл называть резонансной. Вне ее I An/2(i6)v,| >1 и для справедливо асимптотиче
Ское представление
|
21 1 |
![]()
|
(4) |
![]() Lk(I+W+-) (~Т<ат8І<іг)’
Lk(I+W+-) (~Т<ат8І<іг)’
Mv-
|
(N’"T 2|2 С помощью (4) приводим выражение (3) для /„ к виду |
![]() Mi+~K+-)+2Exp{~R) (~т<агг§<-т)-
Mi+~K+-)+2Exp{~R) (~т<агг§<-т)-
(2лУЫ К j Аk, Ex{k,)AnX
|
(5) |
![]() Х(х+5(^)‘ехр(^)) Е^~ш+ікг)-
Х(х+5(^)‘ехр(^)) Е^~ш+ікг)-
Здесь величина 5—1 Для у*<0 при л<аг£$<Зя/2 и для і7*>0 при Зл/2< <аг£$<2я. Вне этих секторов £=0.
Если в скобках в (5) оставить лишь первое слагаемое і/Дя, то выражение для /** примет такой же вид, как и в случае однородного поля. При этом зависимость магнитного поля от координат будет учитываться параметрически. Происхождение второго слагаемого выяснено в [1, 4]. При его интерпретации максвелловское распределение электронов по скоростям удобно представить в виде набора пучков, движущихся вдоль магнитного поля с различными скоростями у*. Каждый пучок, проходя через резонансную зону, обменивается энергией с колебаниями, при этом в нем возбуждаются электрические токи. Эти токи переносятся вместе с пучками вдоль магнитного поля. Поскольку фаза тока совпадает с фазой колебаний в момент прохождения пучка через резонансную зону, а скорости пучков различны, то в одну и ту же точку приходят токи с различными значениями фазы. Очевидно, что интерференция должна приводить к их взаимному уничтожению. Для того чтобы выяснить, на каком расстоянии от резонансной точки это происходит, необходимо проанализировать за
висимость интеграла
1= J^.exp(-igfl + ^l)
— оо
От координаты S (Дп=й)—rc<ц,(s) — Ktvt). Такой анализ был произведен в [1, 4]. Оказалось, что вне сектора —7ji/8<argS<—Л/8 (см. рис. 2) интеграл / становится экспоненциально малым на расстояниях порядка (р.£)ч' От резонансной точки, т. е. практически сразу вне резонансной зоны. Однако в секторе — 7n/8<args<—я/8 интеграл не убывает, а растет с увеличением |s|. Этот результат означает, что мы можем пренебречь вторым слагаемым в скобках в (5), если при нахождении решения будем обходить резонансную точку на достаточно большом расстоянии в верхней полуплоскости комплексного переменного S. Поскольку в нашем случае D(D,/Ds<0, то правило обхода совпадает с правилом обхода Ландау. Следует отметить, что при переходе от максвелловского распределения частиц по скорости к распределениям с меньшим разбросом радиус обхода 6s возрастает. Например, для распределений вида F0{Vt)=CexР (—M(Ut—V0)2/2T) Имеем 6S^V0(L/(D)4,(M/Tyu.
Пренебрегая в (5) вторым слагаемым в скобках и интегрируя по Dvz, Приводим /» к виду
Пшт—т
Ху( (-^г) ) eip (-iat+ikr). (6)
Предположим теперь, что радиус обхода бs превышает также | КгЫ /(д(Т/т)'ь. В этом случае для интеграла вероятности в (6) может быть использовано асимптотическое представление (2). Оставляя в нем два первых слагаемых, приводим /** к виду
/„ = У [АЛа>-п^))]И+к, гТ/т{ы-п(о^))г)ЕЛт)е-ш. т /Lmi
Здесь величина Ап через посредство своего аргумента (см. выше) является дифференциальным оператором, действующим на Ех{Г). Отметим, что при резонансе на основной гармонике электронной циклотронной частоты и при Я<1 выполняется приближенное равенство Ля«1.
Выражение, аналогичное (7), может быть получено и для остальных составляющих плотности тока /«*. В [*] с помощью тензора диэлектрической проницаемости, соответствующего (7), было найдено, что коэффициент поглощения колебаний на основной гармонике циклотронной частоты при Н0 JT V Но равен
Ti=l—ехр (—2Г), (8)
Где
Г=я/4Wc T/Mc2N±KN2(QN)~1 (iV4-2g*-l)2 (N±2+Q-I)~'В~
B= (iVx24-iV*4-2g—3) sin 0 cos <p sin 1|>4- (N±*—G+2) cos 0 cos 1|>,
Q= (cDp./o))1, N=kc/(dy 0=kHo.
Условия, использовавшиеся в [2], при получении (8) сводятся к выполнению одного из двух неравенств: Г<1 или L>(J/m)f/* <o(Af)z cos-11|>, где A*=min ((Д©)"1, (Tv/M)-'UK'*Li)Y Дю — ширина спектра колебаний, v — частота кулоновских соударений. Второе неравенство необходимо для обо
снования возможности использования правила обхода Ландау. Оно означает, что интенсивность случайных воздействий должна быть достаточно высокой. Однако из результатов, полученных в настоящей работе, следует, что на самом деле выражение (8) можно использовать при любой интенсивности случайных воздействий.
ПРИЛОЖЕНИЕ
При получении (1) мы предполагали, что электроны движутся вдоль магнитного поля равномерно. Рассмотрим теперь, останется ли справедливым правило обхода Ландау при ускоренном движении электронов. Будем считать для простоты, что все электроны движутся с одинаковым ускорением А. В этом случае в выражении (1) необходимо произвести замену: Фп-*Фп=Дпт+бт2+ет3, где б=в-А*а/2, е=<ла/6£.
 1т Х
1т Х
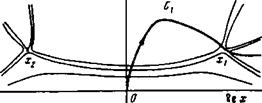
Рис. 3. Контур интегрирования С% при Ьп>0. Тонкие линии - линии действительной фазы подынтегрального выражения
|
|
В отличие от процедуры, использованной выше, удобно сначала вычислить интеграл по <**¥. При этом получаем
^ 01
Тою (2я)1/1 АшЛ *
Где <*хехр(»&п*+^(я:)), (©-»©• (*))/®,
V (Х) - ф* (х+г73а) -1 (х+хг/2а)2, а=*.£, Р-»Ага/2©2, д—Ткяг/2та>2.
Преобразуем /п тройным интегрированием по частям:
TOC o "1-5" h z 7хх=/»}-——X1 [(72.) Та) 1 2л
П«* О»
Где дается (7) и
* <**
Г йжехр(1Ълх) -£^-вхр(*Чж)). (1.3)
о
Интеграл (1.3) удобно вычислить методом перевала. Предположим сначала, что ускорение отсутствует: р«>а—0. Значение интеграла (1.3) определяется начальной
Точкой интервала интегрирования х=0 ж тремя точками перенала: Хх=d„ei;T/e, Хг=
/ ®2 71
=dne5l"/e, Х3=d„e3i*/2t где Dn = ^ j. Линии уровни функции exp(Ibr,X-^F(X))
При Ьп>0, Im Ь„=0 и контур интегрирования С изображены на рис. 3. Точка х=0 дает вклад в интеграл, пропорциональный 1 /Ьпч а точка Ху - пропорциональный exp (-Bndn/2). В результате получаем, что Т<|/п|°°1/Ьп3, и поэтому, как следует из (1.2), /***/2с - Аналогичным образом можно показать, что это приближенное равенство справедливо во всей верхней полуплоскости комплексного переменного S<*>Bn. Однако в некоторой части нижней полуплоскости, а именно в секторе -7я/8< <Arg S-N/8 (см. рис. 2), интеграл Тп растет при |«|-*«>. В этой области Гп^ехр (|Bndn/2). Таким образом, наш анализ подтверждает вывод, сделанный в основном тексте.
Учтем теперь влияние ускорения. Ош* входит лишь в параметр р=&га/2й>2. Естественно предположить, что А~еФ/тЬ где Ф - электрический потенциал, V - размер плазмы. Обычно в плазме Еф~Г, поэтому Ф~крвг/ь'<£1. Следовательно, учет слагаемых, пропорциональных р, в показателе экспоненты F(X) приведет к сдвигу точек перевала на малую величину порядка Такой сдвиг не меняет оценок,
Проведенных выше. Что касается предэкспоненциадьного множителя, то здесь учет ускорения приводит к малым несущественным добавкам, которыми можно пренебречь. В результате мы приходим к заключению, что наличие ускорения не препятствует возможности использования правила обхода Ландау.