ОБРАЗОВАНИЕ ГОРЯЧИХ ЭЛЕКТРОНОВ В ОТКРЫТЫХ ЛОВУШКАХ ПРИ ЭЦР НАГРЕВЕ С ПРОДОЛЬНЫМ ВВОДОМ СВЧ МОЩНОСТИ
Приведены результаты экспериментального изучения популяции горячих ллехтронов. образующейся при ЛДР нагреве плазмы в установке
О ГР А-*. Разработана теоретическая модель, согласованным образом описывающая динамику горячих электронов и распространение электромагнитных колебании по плазме. Результаты, получаемые на основе модели, согласуются с экспериментальными.
Введение
Практически любой эксперимент по ЭЦР нагреву плазмы сопровождается образованием горячих (энергия существенно больше средней энергии основной компоненты плазмы) электронов. В открытых ловушках такие электроны могут определять основное энергосодержание ([}) плазмы.
Несмотря на длительную историю экспериментального и теоретического исследования ЭЦР нагрева плазмы, лишь в последнее время начал выясняться механизм образования популяции горячих электронов. Предлагаемые объяснения этого явления должны ответить на основной вопрос — каким образом поддерживается резонанс между циклотронным вращением, частота которого в процессе ускорения до релятивистских энергий меняется весьма существенно, и электромагнитными колебаниями с очень малой шириной спектральной линии, характерной для современных генераторов, например гиротронов. Естественно надеяться, что, решив эту проблему, мы одновременно поймем, какие факторы определяют энергию горячих электронов, их плотность, распределение в пространстве.
Уже первые эксперименты по ЭЦР нагреву плазмы в открытых ловушках [1—3] показали возможность получения плазмы с [}^0,5 за счет образования группы электронов с энергией свыше 1 МэВ. На этом этапе исследований основное внимание уделялось проблеме МГД устойчивости полученной плазмы. Интерес к механизму образования горячих электронов существенно повысился после возникновения идеи термобарьеров в амбнполярных ловушках и с началом поисков стабилизирующих элементов для акснально-симметричных систем. Так, для успешного функционирования термобарьеров необходимо, чтобы горячие электроны перекрывали все сечение ловушки. Между тем в ряде случаев, как, например, в известных экспериментах на Bumpy-torй [4], горячие электроны образовывали довольно узкие кольпа.
При использовании горячих электронов в стабилизирующих элементах чрезмерный «перегрев» может привести к нежелательным последствиям. Действительно, скорость дрейфа в неоднородном магнитном поле растет с энергией электрона и, если ее величина существенно превышает характерную фазовую скорость желобковых колебаний, то взаимодействие горячих электронов с желобковыми колебаниями ослабляется [5]. В результате стабилизирующий элемент перестает выполнять свою функцию. Именно с такой неприятностью столкнулись в экспериментах на установке TARA [6].
В ходе многолетних исследований был выявлен ряд факторов, существенно влияющих на процесс формирования популяции горячих электронов.
А. Амплитуда электромагнитных колебаний. Установлено (см., наари - мер, [7]), что взаимодействие отдельного электрона, удержизаемого в ловушке, с монохроматической электромагнитной волной принимает хаотический характер (при этом ансамбль электронов будет диффундировать по энергии с известным квазилинейным коэффициентом диффузии), если амплитуда электрического поля превышает некоторое критическое значение Есг~ь*± , где е± —энергия циклотронного вращения электрона. При меньших амплитудах энергия электрона под действием волны испытывает регулярные колебания (движение электрона суперадиабатично и нагрева нет). Из приведенного условия следует, что в электромагнитном поле фиксированной амплитуды энергия электрона не может превысить максимального значения Втах~Е*''- Однако данное ограничение справедливо лишь в идеальной ситуации, когда колебания, используемые для нагрева, действительно монохроматичны, заряженные частицы не сталкиваются друг с другом, плазма спокойна — в ней не возбуждены какие бы то ни было колебания. В реальных экспериментах ни одно из этих условий не выполняется, поэтому нагрев происходит и в области суперадиабатично - сти, а ограничения энергии не наблюдается [8].
При дальнейшем увеличении Е появляется второе критическое значение амплитуды электромагнитной волны. При превышении этого значения коэффициент диффузии электронов по энергии снижается [9]. В этой области значений Е на процессе ЭЦР взаимодействия начинает сказываться релятивистская зависимость циклотронной частоты от энергии электрона. При ЭЦР в однородном магнитном поле влияние данного фактора приводит к тому, что монотонный рост энергии сменяется осцилляциями около некоторого среднего значения. Осцилляции той же самой природы ограничивают ускорение заряженных частиц в циклотроне. Возможно, что указанному эффекту обязано снижение эффективности нагрева с ростом Е, наблюдавшееся в экспериментах [8].
Б. Движение электронов поперек неоднородного магнитного поля_ В том случае, когда частота релятивистских осцилляций превышает характерную частоту изменения магнитного поля на траектории движения электрона в неоднородном магнитном поле, возникает новый адиабатический инвариант, заменяющий магнитный момент [9—11]. При этом медленные изменения магнитного поля приводят к таким изменениям энергии электрона, что для среднего значения энергии выполняется условие циклотронного резонанса Ы=еВс1&, где & — полная энергия электрона с учетом энергии покоя. На этом явлении основан принцип действия синхротронов, где магнитное поле возрастает со временем. В теории ускорителей оно называется автофазировкой. В теории плазмы чаще используется термин релятивистский авторезонанс. В адиабатических ловушках данное явление - может проявляться при циклотронном резонансе с электронами, удерживаемыми вблизи минимума магнитного поля на соответствующих силовых линиях. Если такие электроны смещаются в направлении поперек магнитного поля в сторону его увеличения, то их энергия будет возрастать в соответствии с условием релятивистского авторезонанса (см. выше) [9]. Поперечные смещения электронов могут вызываться НЧ шумовыми колебаниями, постоянными спутниками экспериментов с горячей плазмой. Данный механизм может приводить к образованию колец или дисков горячих электронов, привязанных к медианной плоскости ловушки [4, 12].
В. Ограниченность поперечных размеров СВЧ луча. Этот фактор стано
Вится существенным при выполнении двух условий: ввод СВЧ мощности осуществляется под достаточно большим углом к магнитному полю, и рассеянные СВЧ поля отсутствуют. Предположим, например, что СВЧ луч перпендикулярен силовым линиям магнитного поля и полностью поглощается за одно прохождение через плазму. Если в пределах СВЧ луча магнитное поле меняется в пределах то в соответствии с усло
Вием циклотронного резонанса максимальная энергия, которую может набрать электрон, равна Етах—шсг(В21В1—[). Фактор ограниченности СВЧ луча сказался в экспериментах [13, 14], где средняя энергия горячих электронов соответствовала приведенному выражению для максимальной энергии. Однако в экспериментах [13] наблюдались н электроны с Е>8те». Их появление объяснялось влиянием кулоновских соударений II Отклонением СВЧ луча от перпендикуляра к силовым линиям магнитного поля. Последнее обстоятельство делает необходимым учет эффекта Доплера, видоизменяющего условие циклотронного резонанса с СВЧ колебаниями
Ы=П(йе+к\и\. (1)
Г. Влияние СВЧ фона. Рассеяние увеличивает объем, занятый СВЧ излучением, и тем самым способствует росту етех (см. выше). Если в пределах данного объема величина магнитного поля меняется более чем вдвое, то становится возможным одновременный резонанс на нескольких гармониках циклотронной частоты, тем самым создаются предпосылки для неограниченного разогрева электронов. Роль фона (рассеянного СВЧ излу* чения) продемонстрирована в эксперименте [8]. Заметим, что наличие большого уровня фона было характерно для большинства экспериментов, и только в последнее время проведены эксперименты в условиях малого фона [12—14].
Д. Эффект Доплера. При ЭЦР взаимодействии с колебаниями, у которых Лтц=/с|,с/о)=0, меняется только поперечная энергия электрона. В результате в процессе ускорения траектория электрона стягивается в область меньших значений магнитного поля. По достижении энергии етях~У2ЕцоТпсг, где 8Ц0 — начальная энергия продольного движения, траектория полностью оказывается в области, где (о«<(о, и резонансное взаимодействие прекращается [15]. Ситуация кардинально меняется при N^1, Когда изменение продольной энергии в результате ЭЦР взаимодействия оказывается достаточно большим [16]. В случае Л^=1 ЭЦР взаимодействие проходит в условиях так называемого доплеровского авторезонанса [17, 18] (не путать с релятивистским авторезонансом, см. выше). При доплеровском авторезонансе изменения ех и 8Ц согласованы таким образом, что положение резонансной точки, определяемой условием (1), не меняется с ростом энергии. При этом размах колебаний электрона вдоль ловушки возрастает и ускорение прекращается, когда электрон переваливает через пробку. Нагрев происходит с квазилинейным коэффициентом диффузии по энергии и максимальная энергия, до которой может быть ускорен электрон, равна
Етах=2тс'-(Втах/В-), (2)
Где ВТ — резонансное магнитное поле. То же самое выражение для етв* остается справедливым и при Лгц> 1 [16].
Для электромагнитных колебаний с частотой со^о)«. условие ^Уц>1 выполняется при их распространении вдоль магнитного поля. Продольный ввод СВЧ мощности использовался в экспериментах на установке ОГРА-4. аналнзу которых посвящена данная работа. В настоящих экспериментах энергетический спектр электронов простирался от нескольких десятков эВ до нескольких сотен кэВ. При этом как совсем холодные, так и горячие электроны обнаруживались во всем объеме ловушки от пробки до пробки. Интересно, что холодные электроны не меняли своей энергии лаже в том случае, когда онн проходили через точку ЭЦР. Эти экспериментальные факты послужили основой при формулировке теоретической модели нагрева.
Распределение горячих электронов по всей ловушке, по нашему мнению. свидетельствует о том. что в соответствии с [16] на процесс ускорения определяющее влияние оказывает эффект Доплера (см. выше). Из-за эффекта Доплера точка резонансного взаимодействия горячих электронов сдвигается относительно точки ЭЦР для холодных электронов. Возможна ситуация, при которой большая часть СВЧ энергии, подводимой к плазме, поглощается горячими электронами и не доходит до точки ЭЦР для холодных электронов. В этом случае холодные электроны «выключаются» из
|
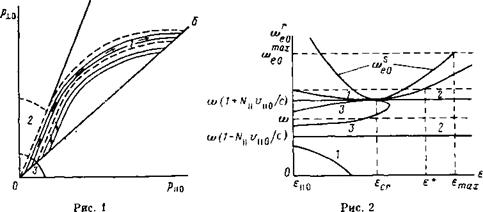
Рис. 1. Популяции электронов, удерживаемых в ловушке: 1 - горячие электроны, 2 - теплые электроны, 3 - холодные электроны; Б - граница конуса потерь, А - граница резонансного конуса, определяемого условием а) = 1ое0; />цо, Ра.о ~ компоненты импульса электрона, отнесенные к центру ловушки |
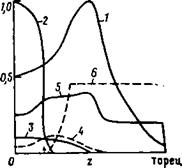
Рис. 2. Зависимости резонансного значения циклотронной частоты а)е0г н циклотронной частоты в точке остановки от энергии электрона для трех значений показателя преломления: 7 — Лгц> 1; 2 - УУц = 1; ^-Агц<1. - максимальное значение
Циклотронной частоты в пробке
Резонансного взаимодействия. На данную возможность указывалось, например, в [19]. Развивая эти идеи, мы в настоящей работе, теоретическая часть которой близка к [20], нашли согласованные распределения горячих электронов по энергии и пространственное распределение электромагнитного поля. Характерно, что в стационарном состоянии ни функция распределения электронов, ни полное энергосодержание плазмы не зависят от вводимой СВЧ мощности. Объясняется это тем, что как нагрев электронов, так и их потери из ловушки есть следствия одного и того же физического явления — СВЧ диффузии по энергин при ЭЦР нагреве.
В первом разделе приведем характеристики установки ОГРА-4 п основные экспериментальные результаты, обосновывающие теоретическую модель. Теоретический анализ приведен во втором разделе, обсуждение результатов экспериментов на основе теоретической модели проводится в третьем. В Заключении сформулированы основные выводы.
1. ЭЦР в установке ОГРА-4
Установка ОГРА-4 представляет собой сверхпроводящую магнитную систему типа бейсбол (одиночная открытая ловушка с минимумом магнитного поля) с пробочным отношением (продольным и поперечным) ~2 [21]. Величина поля была такой, что в ловушке осуществлялся ЭЦР для излучения гиротрона с длнной волны 8 мм. Мощность гиротрона достигала 200 кВт при длительности работы 50 мс.
При СВЧ пробое водорода при давлении (1—5) • 10_в мм рт. ст. образовывалась электронно-горячая плазма с (^10% [21—23]. Изучение этой плазмы показало наличие трех групп электронов: холодные, теплые и горячие. Будет обозначать их плотность П1’Ю, Л и среднюю энергию.
Холодные электроны возникают в результате ионизации нейтрального газа. Поскольку до точки ЭЦР доходит лишь малая часть СВЧ мощности, то холодные электроны весьма слабо взаимодействуют с электромагнитными колебаниями. Более существенно на их поведение влияют амбпполяр - ный потенциал [21] и кулоновские соударения. Под действием соударений холодные электроны выбрасываются из ловушки. В то же время их небольшая часть попадает в область фазового пространства, где влияние СВЧ диффузии преобладает над соударениями. Эти электроны вовлекаются в процесс ускорения, образуя высокоэнергичный «хвост» функции рас-
|
Плотность плазмы в центре п, 1013 см-1 |
0,5 |
|
Отношение П/пя в центре, 10[89] |
5 |
|
Плотность теплых электронов Пс* 1013 см-3 |
0,5 |
|
Средняя энергия Ее*, кэВ |
1-3 |
|
Характерный диаметр области с теплыми электронами (на уровне 0,1), см |
16 |
|
Объем тепло» плазмы, л |
5 |
|
Плотность холодных электронов Пес, 10“ см-3 |
1-4 |
|
Средняя энергия есс, эВ |
20-80 |
|
Характерный диаметр области с холодными электронами, см |
32 |
|
Плотность горячих электронов ПвА, 1012 см~3 |
0,8-1,5 |
|
Средняя энергия горячих электронов еД МэВ |
0,1-0,4 |
|
Характерный диаметр области с горячими электронами, см |
32 |
|
Объем горячей плазмы, л Максимальное р, % (ток в бейсболе 1,3 к А) |
20 |
|
15 |
|
|
Максимальное удельное энергосодержание, кДж/м3 |
100 |
|
Энергетическое время жизни теплых электронов, мс |
1 |
|
Характерное время жизни холодных электронов, мкс |
10 |
|
Характерное время жизни горячих электронов, с |
0,5 |
|
Средняя энергия ионов е, эВ |
10-40 |
|
Потенциал плазмы, В |
+ 150-300 |
|
Продольный плазменный ток, А |
2 |
|
Примечание, п^ — плотность нейтральных атомов. |
Чае. Поскольку в описываемом эксперименте холодные электроны проходили через всю ловушку, то электромагнитное поле должно практически полностью поглощаться на горячих электронах, не доходя до точки ЭЦР холодных. Измерение большого коэффициента поглощения на горячих электронах, проведенное методом СВЧ просвечивания после выключения гиротрона, когда в ловушке удерживаются только горячие электроны, подтверждает сделанное объяснение.
Измерения, проведенные с использованием болометров [24], показали, что большой коэффициент поглощения за один проход обеспечил малый уровень СВЧ фона в камере при работе гпротрона.
Опыт показывает, что процесс ЭЦР нагрева плазмы определяется горячими электронами. Что касается популяций холодных и теплых электронов, то они играют роль резервуара, из которого черпаются электроны, вовлекаемые в процесс ускорения. Цель настоящего раздела — теоретическое описание динамики горячих электронов. Для того чтобы получить замкнутую картину ЭЦР нагрева, необходимо также рассмотреть распростране
Ние электромагнитных колебаний по плазме.
При ЭЦР взаимодействии с монохроматическими электромагнитными колебаниями остается постоянной величина
Г—|i(D=const, (3)
Где ^.=6^/(1)*, Const=e|[0 Определяется начальной (до ускорения) продольной энергией теплых (холодных) электронов. Это соотношение позволяет проследить за смещением точки отражения (остановки) электрона от магнитной пробки Z« в процессе нагрева
Соео* — е|,о/ц+й)4-цй)2/2тс (4)
Здесь и в дальнейшем Ь),0(z) — электронная циклотронная частота, рассчитанная по массе покоя электрона, индекс 5 отмечает значения величин в точке остановки электрона, индекс г—в точке резонанса (см. (1)). Точка нерелятивистского ЭЦР, определяемая условием (i)=coe0, Обозначается через Zro.
Из соотношения (4) следует, что до тех пор пока энергия поперечного движения электрона мало по сравнению с Тс2, рост ц сопровождается «подтягиванием» точки остановки электрона Z, К точке Zr0. При этом разброс в положениях точек остановки, связанный с разбросом в значениях Е (!о, сокращается. Этот процесс ведет к образованию популяции «плещущихся» электронов, (см., например. [7]). Однако при превышении энергией критического значения ЕГГ точка остановки 2, начинает удаляться от точки ZRО (рис. 2).
Что касается положения резонансной точки Zr, То оно изменяется по - разному в зависимости от значения N< (см. рис. 2). Если Л^<1 (такие значения N{] Характерны для ввода СВЧ луча под большими углами к магнитному полю), то траектории двух резонансных точек Sr, Соответствующих разным знакам Vy, При некотором значении энергии пересекаются. Эта энергия является максимальной, до которой могут быть ускорены электроны. При W„<1 Для £тах имеется простое выражение [15, 16]
Emix—e. cr=V2e;|0Mc2. (5)
При N,|=1 Ускорение определяется явлением доплеровского авторезонанса [17, 18]. В этом случае е..( и при взаимодействии с волной меняются таким образом, что резонансная точка не сдвигается. Что касается точки остановки Z„ То по мере нагрева она сначала смещается к центру ловушки. Однако, достигнув резонансной точки «г. точка начинает сдвигаться по направлении к пробке. Нагрей прекращается, когда точка остановки достигнет максимума магнитного поля в пробке и частица покинет ловушку. Соответствующее значение максимальной энергии, как следует из (4), дается выражением (2) [16]. Это выражение для Em*x Остается справедливым и при Лц>1. Отметим, что в последнем случае резонансная точка в процессе нагрева не остается неподвижной (см. рис. 2).
Показатель преломления правополяризованных колебаний, распространяющихся вдоль магнитного поля, дается выражением
N2=N{[z2zi--(щp'C2/(щ (о)ео—аз). (6)
Здесь о)Р/ — электронная' плазменная частота, рассчитанная по плотности холодны.'; электронов Пес. Из приведенных на рис. 2 двух кривых для случая А >1 реальное значение в эксперименте имеет лишь верхняя, так как в область пространства, где должен был бы осуществляться резонанс, соответствующий нижней кривой, электромагнитная волна практически не доходит (точка Zr Находится ближе к центру ловушки, чем Zro). В силу того, что в экспериментальных условиях NЧ является функцией координаты Z. найти явный вид зависимости а)е0г от е в общем случае не представляется возможным. В то же время сравнительно простой оказывается обратная зависимость е от циклотронной частоты о)<.0г н показателя преломления N/=N:zr) В точке ЭЦР:
Е±=тс~ I (ь^oVь))— 1 Dh --- ----- V (ь)e0R/(i))2+l—2(ь)e07ы)) (l+e„0//nc2)l.
L }NTl-1 J
(7)
Здесь двум знакам отвечают два участка кривой (ое0г на рис. 2 при е> >есг( + ) и е<есг( —). При этом на участке ( + ) с волной взаимодействуют электроны, догоняющие волну, а на участке ( —) движущиеся навстречу волне. На рис. 2 видно, что существует энергия е*, ниже которой резонансное условие выполняется в двух точках, тогда как при е>е* остается только одна. Величина энергии е* зависит от плотности холодных электронов и может быть легко определена пз уравнений (6), (7).
Рассмотрим установление функции распределения горячих электронов при ЭЦР. Воспользуемся тем указанным выше обстоятельством, что при ЭЦР диффузия на плоскости е. ц осуществляется вдоль линий (3). Каждому значению начальной энергии 8Ц0 соответствует своя линия. Естественно считать, что как средняя величина еь0, так и разброс в значениях Elie Совпадают со средней энергией ев”с теплых (холодных) электронов. При рассмотрении энергетических интервалов, значительно превышающих ее" можно приближенно считать, что все электроны располагаются на одной линии. Это позволяет заменить двумерное уравнение Фоккера — Планка одномерным (см. рис. 1).
Будем считать, что амплитуда СВЧ поля в точке циклотронного резонанса ЕТ достаточно велика, так что эволюция функции распределения горячих электронов /(е) описывается квазилинейным уравнением диффузии
TOC o "1-5" h z Df Д Df
77-TD1T=4' (8)
Ot de de
Где D=e2C4/r2£г2Й){,/4^2|Ф''| — коэффициент диффузии (см. [7] ),
| ф " | =mc4P||(§r-21 Мм +<ыiV||'pii/Me—Ь)eo'N „цои/ер,, | Г, штрих обозначает производную по Z,
&’=е--пгс2, ыь=(с21Ь&’)Утцые0(0)
— Частота колебаний электрона вдоль магнитного поля при параболическом профиле магнитного поля с характерным масштабом Ь, рх, ц — поперечный и продольный импульсы электрона, величина Д характеризует источники частиц. В нашей модели величина Ц отлична от нуля и положительна в области низких энергий е~еЛс.
Справедливость квазилинейного уравнения (8) обсуждается в Приложении 1.
В стационарном режиме на участке, свободном от источников и стоков, имеем
ДЦд*= - кт, (9)
Где Л — поток частиц по оси энергии. Функция распределения горячих электронов может быть найдена прямым интегрированием соотношения (9). Однако коэффициент диффузии /) зависит от амплитуды волны в резонансной точке, которую в силу (7) следует считать функцией энергии.
Определим зависимость Ег(гг{е)). Для того чтобы рассчитать затухание волны на горячих электронах при распространении вдоль оси ловуш« ки, используем закон сохранения энергии в форме
С*5№= - Ие (Я*;)/2, 5=(сДГ/4л)£2. (10)
Здесь 5 — поток СВЧ энергии, / — ток, возбуждаемый волной в плазме. Расчет / по стандартной методике [7] приводит к следующему выражению для возмущения функции распределения горячих электронов [ под действием СВЧ колебаний:
^------- (——Г'{~т~ +сВ~1(^1-к»и<>/ы'>т-) •
((о—(*)<»—лц1?„) ' е Дг дц'
Как было указано выше, считаем, что для всех электронов постоянная в правой части (3) имеет одно значение е |]0 и поэтому для / в (11) справедливо выражение (см. Приложение 2)
/(е. ц, г)=/(е)б(ц - 8 (12)
' а) 7 яг;,,
Здесь б — дельта-функция. Используя (10)— (12), находим, с.,, - Е2Е, гр±шь2с‘ й}
ЙоНъ I V 2 4 1 У] (13)
Особенность в правой части (13) при Л^=1 обусловлена явлением до-
Плеровского авторезонанса (положение Ът не зависит от энергии и, следовательно, в этой точке должно сосредотачиваться все поглощение).
При е>е* мы имеем однозначную связь энергии е и 2 (7), что позволя
Ет преобразовать (13) к виду
Й5/йе+= — Ш//с2е=/е. (14)
При е<е* резонанс происходит в двух точках (см. рис. 2) и выражение (14) принимает следующий вид (используется связь е+ и Г)
Соотношения (14) —(15) соответствуют закону сохранения энергии. Уравнения (9), (14), (15) согласованным образом описывают стационарный режим нагрева горячих электронов и затуханпя электромагнитных колебаний.
Из (14) можно оценить поток энергии, поглощаемый горячими электронами 5,1=Уе(етвх—ев“с), где Сто* дается формулой (2). Эта велпчина не может превышать потока электромагнитной энергпп на выходе из СВЧ излучателя 5о. Предполагая, что холодным электронам передается малая доля А СВЧ мощности, получаем £*= (1—а)£„. На рпс. 3 показан пример расчета зависимости потока 5 от величины локального пробочного отношения 7?(г) =2?(г)/2?(0) для конкретных значений параметров п зависимостей. указанных в подппсп к рисунку н близких к нашнм экспериментальным условиям. Сравнение рассчитанной функцпи распределения / с экспериментом приводится ниже.
В стационарном состоянип функция распределенпя горячих электронов оказывается независимой от амплитуды электромагнитного поля, падаю-
|
Рис. 4 |
|
Рис. 5 Рис. 6 |
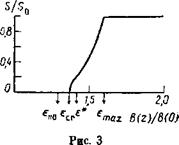 Рис. 3. Зависимость потока электромагнитной энергии S от локального пробочного отношения B(Z)/B(0). Стрелками отмечено положение ЭЦР для указанных энергий электронов. Значения параметров расчета: B(Z) =В(0) (1+ (Z/L)2), Nec(Z)—Ne0С(1,1— (Z/L)Z), В(0) = 1 Тл, Tieoc = 10'1 см-3, ецо=0,5 кэВ, а=0,01. Пробочное отношение ловушки В Max!В (0)=2
Рис. 3. Зависимость потока электромагнитной энергии S от локального пробочного отношения B(Z)/B(0). Стрелками отмечено положение ЭЦР для указанных энергий электронов. Значения параметров расчета: B(Z) =В(0) (1+ (Z/L)2), Nec(Z)—Ne0С(1,1— (Z/L)Z), В(0) = 1 Тл, Tieoc = 10'1 см-3, ецо=0,5 кэВ, а=0,01. Пробочное отношение ловушки В Max!В (0)=2
Рис. 4. Зависимости от координаты Z (без масштаба): 1 - магнитное поле (нормировано на поле в пробке); 2 - плотность теплых электронов (нормирована на Птах= = 51012 см-3); 3, 4 - плотности горячих и холодных электронов (нормированы на Яшах); 5 - потенциал плазмы (нормирован на 1 кВ); 6 - мощность СВЧ (см. рис. 3). Стрелка - точка ЭЦР для холодных электронов
Рис. 5. Осциллограммы: А - линейная плотность Nl, Б — поток электронов на торец с энергией более 0,4 кэВ, В — мощность гиротрона
Рис. 6. Осциллограмма потока горячих электронов на торец: А — показания рентгеновского датчика, Б - мощность гиротрона
Щего на плазму. Можно рассчитать энергосодержание популяции горячих электронов (Ne)H, которое тоже не зависит от вводимой СВЧ мощности и дается выражением
TOC o "1-5" h z ЕТах е
(Ne)H= ™ С ” G, G= J Cfggj Didj/Dt, (16)
2л EzL
*110 e,10
Где чертой отмечены безразмерные величины е/гас2 и Fmcz, // — характерный размер изменения магнитного поля. Интеграл G По порядку величины близок к единице. Независимость стационарных значений функции распределения и энергосодержания по Е отражает тот факт, что как ускорение, так и потери горячих электронов определяются СВЧ диффузией.
Расчеты показывают, что G слабо зависит от плотности холодных электронов Пес. Более существенна зависимость G от соотношения между частотой колебаний а) и максимальной циклотронной частотой в пробке о)е,„ох (см. ниже).
3. Результаты экспериментов и их обсуждение
Многие экспериментальные результаты были использованы при построении теоретической модели и, естественно, согласуются с ней. Кратко суммируем их. Модель хорошо описывает следующие экспериментальные факты:
— Распределение горячих электронов вплоть до пробок;
— Поглощение основной части СВЧ мощности на горячих электронах и слабый нагрев холодных электронов;
— Образование трех групп электронов: холодные, теплые и горячие. Подробнее обсудим последнее заключение. Если причины появления и взаимодействия холодных и горячих электронов были обсуждены выше достаточно подробно (см. рис. 1), то выделение специальной промежуточной группы требует пояснения.
Обратимся к фазовой плоскости переменных Р±0, рц0 (см. рис. 1). На ней тонкими линиями изображены траектории, по которым диффундируют электроны под действием СВЧ поля. В нерелятпвистской области они близки к прямым, параллельным резонансному конусу (линия а), и пересекают конус потерь (линия Б) в области малых энергий. Если при всех значениях энергии фазовая плотность электронов на линии Б обращается в нуль, то основным результатом СВЧ диффузии будет выброс электронов из ловушки. Для того чтобы возник поток электронов, направленный в сторону больших энергий, т. е. СВЧ диффузия приводила к нагреву, фазовая плотность электронов в области малых энергий должна поддерживаться немагнитным способом. На рис. 4 показаны продольные зависимости магнитного поля, потенциала, СВЧ мощности и плотностей трех групп электронов в эксперименте ОГРА-4. Видно, что холодные электроны, слабо взаимодействующие с СВЧ волной, удерживаются самосогласованным амбиполярным потенциалом и имеют максвелловскую функцию распределения. Холодные электроны, «вытягиваемые» СВЧ полем, образуют на фазовой плоскости «струю», параллельную резонансному конусу (при нерелятивистских энергиях). В координатном пространстве ей соответствует популяция плещущихся электронов.
Кулоновские столкновения размывают «струю» в поперечном направлении. Электроны, попадающие внутрь резонансного конуса, образуют группу теплых. Основная часть теплых электронов непосредственно не взаимодействует с СВЧ полем, так как при своем движении вдоль ловушки онп не доходят до точки ЭЦР (см. рис. 4). Энергетический баланс теплых электронов определяется нагревом на «струе» н охлаждением на холодных электронах. Фазовый объем, занимаемый теплыми электронами, велик (см. рис. 1). Поэтому прп сравнимых фазовых плотностях электро* нов в областях 2 и 3 число теплых электронов в ловушке может существенно превышать число холодных, что и имело место в эксперименте.
Кулоновское размытие «струп» происходит не только в резонансный конус, но и в другую сторону. Этот процесс приводит к попаданию электронов на линии СВЧ диффузпп. пересекающие конус потерь, и, следовательно, к выбросу электронов из ловушки. Из рис. 1 видно, что энергия теряемых электронов может значительно превышать энергию холодных и быть значительно меньше энергии теплых. Вполне естественно, что поток из ловушки резко ослабевает в момент выключения гиротрона (рис. 5). После этого основной поток электронов из ловушки определяется кулонов - скпм распадом популяции теплых электронов.
Описанные качественные соображения объясняют ряд экспериментально наблюдаемых фактов: резкий сброс потока теплых электронов прп выключении гпротрона прп отсутствии сброса их плотности (см. рис. 5); более нпзкая энергия теплых электропов в потоке из ловушкп по сравнению с измеряемой в центре плазмы методом томсоновского рассеяния; ха-
|
Рис. 7 |
|
Рис. 9 |
 КЕ)
КЕ)
|
|
|
|
|
Рис. 8 |
 НЕ)
НЕ)
Рис. 7. Относительные изменения диамагнитного сигнала Б (сплошная линия) и циклотронного излучения (1 — регистрация в направлении, нормальном к магнитному полю; тип волны необыкновенный, длина волны 1,95 мм). Стрелка — момент
Выключения гиротрона
Рпс. 3. Энергетический спектр горячих электронов: расчет — сплошная линия (резонансное пробочное отношение 1.6, ецо=0,5 кэВ, а=0,01); эксперимент - линия с кружками (а — рентгеновский фотоэлектронный спектрометр, Б — рентгеновский анализатор)
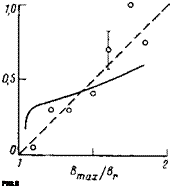
Рис. 9. Зависимость функции G/2 в формуле (16) от Втах1Вг (сплошная линия) и измеренные величины диамагнитного сигнала (кружки) (отн. ед.). Штриховая линия -
(Втах/Вг—1)
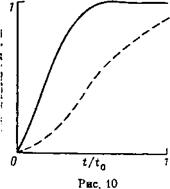
Рис. 10. Расчет динамики изменения средней энергии (1) и плотности (2) горячих
Электронов
Рактерное время жизни теплых электронов близко к кулоновскому; сосредоточенность теплых электронов внутри резонансной поверхности. Разумеется, приведенные соображения станут доказательными лишь после подтверждения численными расчетами, основанными на решении двумерного уравнениня Фоккера — Планка.
Модель предсказывает выброс горячих электронов вдоль осп ловушки через пробку, который существенно превышает классический столкновп-
тельный поток в конус потерь. Понятно, что при выключении гиротрона СВЧ выброс горячих электронов мгновенно прекращается (выключается СВЧ диффузия). На рис. 6 показана полученная рентгеновским датчиком, осциллограмма потока горячих электронов на торец, подтверждающая модель. Сигнал диамагнитной катушки не имеет сброса в момент выключения гиротрона (рис. 7), и плотность горячих электронов не изменяется в этот момент. Из рис. 6 видно, что включение гиротрона увеличивает торцевой поток горячих электронов более чем в 20 раз.
Модель вполне удовлетворительно предсказывает энергетический спектр горячих электронов. На рис. 8 приведено сравнение расчета с экспериментом при использовании двух различных методик рентгеновских измерений в различных диапазонах энергии. Хорошо совпадает не только значение Етах, которое дается формулой (2), но и пологая форма спектра.
Рисунок 9 позволяет сравнить рассчитанную зависимость функции £ в формуле (16) от отношения Втах/Вг с экспериментально наблюдаемой зависимостью диамагнитного сигнала. Видна правильная тенденция изменения, связанная, в частности, с уменьшением етах (2).
Оценим величину давления плазмы по формуле (16) в конкретных условиях эксперимента ОГРА-4. Используя значения £=25 см, а)=2,4- •1011 с"1, получим (пе)л—1017 см“3 эВ, что близко к экспериментально наблюдаемым значениям (см. таблицу). Интересно, что формула (16), дающая предельно достижимое энергосодержание при ЭЦР нагреве, содержит лишь два экспериментальных параметра: характерный масштаб изменения магнитного поля и частоту. Из нее, в частности, следует, что с ростом величины магнитного поля возрастает предельное энергосодержание плазмы, но падает предельно достижимое значение р. Это объясняет, в частности, тот факт, что большие во многпх экспериментах легко получались при малых магнитных полях. Рост предельного энергосодержания при уменьшении характерного размера изменения магнитного поля связан с уменьшением коэффициента диффузии /), см. (8), т. е. с уменьшением потерь горячих электронов. Следует отметить, что характерный масштаб изменения магнитного поля не совпадает с размером ловушки. Это обстоятельство позволяет менять длину ловушки без изменения предельной величины энергосодержання.
На рис. 7 видна динамика нагрева горячих электронов. На нем показано сравнение диамагнитного сигнала с сигналом циклотронного излучения на высоких гармониках о)в. Известно, что интенсивность излучения пропорциональна (яе',) где v>l. Поэтому совпадение двух сигналов свидетельствует о преимущественном увеличении плотности горячих электронов. Эта тенденция следует из рассмотренной теоретической модели. Определяя среднюю энергию горячих электронов из наклона логарифма функции распределения и среднюю плотность горячих электронов из величины функции распределения при энергни е„,„/2, рассчитаем характер изменения этих величин (рис. 10). Из рисунка видно, что изменение плотности более медленное.
Можно оценнть время установления диамагнитного сигнала по порядку величины, воспользовавшись усредненным коэффициентом СВЧ диффузии (8):
Т~тО)Ета*/е£2Е||0. (17)
Видна наблюдаемая во всех экспериментах обратно пропорциональная зависимость времени нарастания диамагннтного сигнала от мощности СВЧ. Используя параметры эксперимента на установке ОГРА-4 (£^1 кВ/см), оцениваем величину т в диапазоне 0.01—0,1 с. что находится в соответствии с экспериментом (см. рис. 6, 7).
Холодные и теплые электроны, появнвшпеся в результате ионизации газа, служат источником частиц в процессе ускорения до болыппх энергий. Из простых соотношений можпо оценнть. какая доля ионизационного потока частиц захватывается в процесс ускорения. Оказывается, что при
” «"ттподе при давлении 210~в мм рт. ст. в установке ОГРА-4
Захватывается меньше 1%. Такой малый источник холодных электронов, необходимый для поддержания процесса нагрева горячих электронов, существует и после выключения гиротрона из-за ионизации на остаточном газе. Это объясняет, почему при повторном включении гпротрона через
0, 5 с после выключения подачи газа и первого импульса гпротрона наблюдался нагрев (рост диамагнитного сигнала), а не быстрый распад плазмы из-за СВЧ диффузии.
Заключение
Проведенные теоретические и экспериментальные исследования показывают, что образование горячих электронов при ЭЦР в неоднородном магнитном поле при продольном вводе СВЧ мощности может быть описано моделью, в которой учтены влияние эффекта Доплера на ЭЦР и изменение амплитуды электромагнитной волны из-за поглощения на горячих электронах. В модель вводятся два параметра: начальная энергия электронов е 0 И доля СВЧ мощности а, передаваемая холодным (теплым) электронам. Подбор на основе экспериментальных данных значений указанных параметров позволяет получить хорошее количественное соответствие теоретических результатов с экспериментальными. Теоретический расчет е,0 и а возможен лишь в законченной теории ЭЦР нагрева, описывающей динамику всех трех групп электронов. Поскольку на поведение низкоэнергичных электронов (холодных и теплых) существенное воздействие оказывают ку - лоновские столкновения, такая теория требует решения двумерного уравнения Фоккера — Планка.
Практически важными результатами настоящего исследования являются определение максимальной энергии электронов и максимального энергосодержания плазмы в открытых ловушках, а также вывод о возможности управления этими параметрами. Последнее особенно существенно при использовании ЭЦР нагрева в стабилизирующих элементах амбипо- лярных ловушек.
За обсуждения работы авторы благодарят А. В. Звонкова.
ПРИЛОЖЕНИЕ 1
О диффузионном уравнении. В отсутствие случайных воздействий диффузионное уравнение (8) непригодно для описания эволюции функции распределения электронов в суперадиабатической области (см. Введение). В обсуждаемых экспериментах граница этой области проходит при энергии порядка максимальной наблюдаемой (—100 кэВ). Однако справедливость диффузионного уравнения (8) восстанавливается, если кулоновские столкновения или какие-то иные случайные воздействия «сбивают» фазу ларморовского вращения электрона за время между двумя прохождениями через резонансную зону. Оценки показывают, что в условиях обсуждаемых экспериментов интенсивность кулоновских столкновений близка к тому значению, которое достаточно для полной декорреляции фазы ларморовского вращения. Отметим, что частичное сохранение фазовой корреляции приводит не к прекращению диффузии, а лишь к уменьшению коэффициента диффузии [7]. В условиях обсуждаемых экспериментов коэффициент диффузии если и снизился, то не слишком существенно. Действительно, в них (см. разд. 1) наблюдалось полное поглощение право- иолярнзованных электромагнитных колебаний в заведомо суперадиабатическом режиме - амплитуда колебаний была на четыре порядка меньше по сравнению с использованными для нагрева.
В приведенном в разд. 2 выражении для коэффициента диффузии баунс-частота является одним из сомножителей, а сам коэффициент диффузии входит в (8) под знак производной по энергии. В некоторых первоначальных работах (см., например. [25]) зависимость баунс-частоты от энергии не учитывалась и, соответственно сама пта величина выносилась из-под знака производной. Нетрудно показать [261, что последовательный учет такой зависимости приводит к диффузионному уравнению вида (8).
П Р И Л О Ж Е Н И Е 2
Функция распределения электронов в адиабатических ловушках. Состояние электрона в адиабатической ловушке удобно характеризовать поперечным и продольным адиабатическими инвариантами - ц, 7ц и соответствующими фазами - Ф^. Фн. (Дрейфовое движение поперек магнитного поля для интересующей нас проблемы несущественно.) Стационарная функция распределения не должна зависеть от фаз Ф_1_. Фп, поэтому число частиц в элементе фазового объема дается выражением
^дг=^(ц, /„М^/^Ф^Фн. (П.2.1)
Выразим в (П.2.1) величину /ц чср^з интегралы движения ц, є и перейдем от фазы Фн к координате г. Используя соотношение с? Фц/<іг=озь>ц, приводим (П2.1) к виду
СІУ—Л7(ц, е)^Ц^е^-и)б/.*11-|;,
Где N — полное число частиц, приходящееся на единичное поперечное сечение ловушки, функция /(ц, е) нормирована на единицу.