К ВОПРОСУ ОБ АНОМАЛЬНОМ ЭЛЕКТРИЧЕСКОМ ПОЛЕ В ЗАМАГНИЧЕННОЙ СЛАБОИОДШЗОВАННОЙ ПЛАЗМЕ
М. И. БЕЛАВИН, А. В. ТИМОФЕЕВ, Б. Н. ШВИЛКИН
I. ВВЕДЕНИЕ
Как известно, в стационарном газовом разряде возникает электрическое поле, называемое амбиполярным, функцией которого является уравнивание потоков частиц с разными знаками зарядов. Если разряд помещен в магнитное поле, то амбиполярное электрическое поле часто отличается по величине, а иногда даже по знаку от рассчитанного в предположении «классического» характера диффузии заряженных частиц (см., например, [1_3]). Разряд в магнитном поле отличается также легкостью, с которой в нем самопроизвольно возбуждаются колебания электрического поля. Представляется естественным связать эти две особенности в поведении разряда. Действительно, поскольку в слабоионизованной плазме газового разряда электроны и ионы под действием колебаний,, вообще говоря, движутся с разной скоростью, то для уравнивания дополнительных потоков, вызванных колебаниями, должно потребоваться измененное значение амбиполярного электрического поля.
Аномалии в поведении амбиполярного электрического поля становятся особенно заметными в области параметров разряда, характеризуемой соотношениями рт. е. в «момент замагничивания» ионной ком
Поненты плазмы. Здесь ю* — ионная циклотронная частота, V* — частота ион-нейтральных столкновений, р< — ионный ларморовский радиус, А — Радиус разрядной трубки. В этой области параметров развивается специфическая разновидность дрейфово-диссипативной неустойчивости — так называемая низкочастотная дрейфовая неустойчивость. Линейная теория этой неустойчивости была развита в [4] (см. также обзорную работу [5]К Она довольно удовлетворительно согласуется с результатами экспериментов. В теоретической части настоящей работы в квадратичном по амплитуде электрического поля приближении рассмотрено движение плазмы под действием колебаний. Анализ проводился в рамках той же модели, что и использовавшаяся в [4]. Найдено изменение амбиполярного электрического поля, вызываемое движением заряженных частиц. Рассчитанное значение амбиполярного электрического поля удовлетворительно согласуется с данными эксперимента. Теория также объясняет и общий характер зависимости амбиполярного электрического поля от магнитного. При расчетах колебания предполагались регулярными.
Отметим, что в разряде наряду с регулярными возбуждались и шумовые колебания. Однако последние имели существенно иные волновые характеристики, а область параметров, в которой они наблюдались, была значительно более широкой. По-видимому, шумовые колебания принадлежат к ионно-звуковой ветке дрейфово-диссипативной неустойчивости. Для того чтобы выделить эффекты, вызываемые регулярными дрейфовыми колебаниями, пришлось использовать специальную технику (обратные связи, модуляция ВЧ-напряжения, питающего разряд).
В настоящей работе анализ движения ионов производился тем же способом и прн тех же упрощениях, что ив [4]. Основными из них являются: использование разложения по отношению р*/а, которое предполагается малым (в экспериментальных условиях величина рДа менялась в пределах - от 0,1 до 1), а также представление пространственной зависимости колеблющихся величин в так называемом локальном квазикласси- ческом виде ~ехр(—ШЬ+ікуу+ік^). Используется локальная декартова система координат, ось X которой направлена по радиусу разрядной трубки, ось У — по азимуту, ось Ъ — вдоль трубки (параллельно магнитному полю). Главное отличие от [4] состоит в том, что при решении кинетического уравнения для ионов мы проделали еще одну итерацию по малой амплитуде колебаний.
Кинетическое уравнение, использовавшееся в [4], имеет вид
-Г7+ (▼?)/ + —(-У«р + ——вц/), (1)
01 т с / Оу
Где 8Ц/)=-^<(/-/оо)+ V* — /оо Г (/-/оо)^У,
По
П«»«ехр(-7-(-!у^ + *ф0(*>)).
Ф=ф0 (я) +ф! сое (Ы—куу).
В дрейфовых колебаниях поэтому влияние Е1г на движение ионов
Не учитывается и для простоты в (1) считается Кг=0.
В начальном, невозмущенном состоянии имеем:
TOC o "1-5" h z 4 4 I АЛ. /9ч
/о^/оо І 1+Хі------- —-—-—I, (2)
(о* /
Хде х<=п0д7лоо=х+ефо7^<, х=л07л0. В первом приближении по фі получаем:
1 °°
Л = — ехр(—Ш+ікуу—І/сур< зіп а)/оо У, ^п(кур{)Х £
П»— оо
X е, па(—і(ш—яю^+Уі)-1 (- —то, фі +
Т І
TOC o "1-5" h z С а)42 П,
+ — ІкуКі—^фі+уі —) +С. С. , (3)
Н ©.-Ч^,2 П0 /
Где а — азимутальный угол в пространстве скоростей, р*=17х/й)*,
И±=к(ияг+иуг)4*, ]п - функция Бесселя индекса П. Выражение (3) исполь
Зовалось в [4] при выводе дисперсионного уравнения низкочастотных дрейфовых колебаний.
В следующем приближении находим
Ов
И=-^7-ку — іОофі V еі("“т)а(—Цю-лш. ОН^)-1 х
4 Тпі 1
Л,»и»— оо
|
( |
Ефі С (Ні1
-ітШі —- + ІкуУіі —— -2 фі +
7 і /і (і) і тУі
Здесь для краткости опущен аргумент функций Бесселя. Отметим, что мы привели лишь постоянную часть /2, которая определяет дополнительный поток ионов, связанный с колебаниями.
Помножив (4) на V. и проинтегрировав по скоростям, получаем:
6Jix=------------------------- IT-Г У (-t(«-no.,)+v,)- X
16лГ, D)(J+Vi2
П* — 00
00 —1 Х[1-+с'с- (5)
Оо
СТ х со i2
Здесь o),*=A:yXi—--------- ——- — ионная дрейфовая частота, £п=ехр(—£)/«(£),
Еп (Hi 'TVi
%=Tikvz/(rriiWi2), /„ — модифицированная функция Бесселя индекса п. Отметим, что движение ионов под действием нерегулярных колебаний можно также описывать выражением (5), произведя в нем замену ©-♦ю-Нт“1, где т — характерное время сбоя фазы колебаний.
1. Механизмы выноса ионов
А. Диффузия ионов в колебаниях
Выясним сначала, каким физическим процессам обязана та часть потока б/*,, которая пропорциональна ©Л Учитывая, что ©/ в свою очередь
Dn Оо
Пропорциональна Xi оэ---------- , представим эту часть потока в виде
Dx
ЫР—В^. (6>
Dx
Предположим, ЧТО ВЫПОЛНЯЮТСЯ условия ©>V„ &ур<<1; тогда для
Dt получаем следующее приближенное выражение:
В, Я,~2 (ткуЪ) [■^Ч^Г + Т(Л, Р,)г (ш-ш. Г+у,']’ (7>
Где б=ky2pitVi=Di±kyl, Di^TivJniitoi — коэффициент диффузии ионов в направлении поперек магнитного поля, р*2=7/т*©Д
Проанализируем сначала диффузию в низкочастотных колебаниях (©<©*). Используя выражение для скорости дрейфа в скрещенных полях, получаем:
<
Дх (t) = Х (t) - Х (0) = К, f <р, (t.) Dt,. (8)
Н о
Предположим, что функция <pi(f) является случайной, тогда дисперсия в значениях координаты Х Будет возрастать со временем и, следовательно, частицы будут диффундировать по ОХ. Из (8) находим выражение для дисперсии:
2 TOC o "1-5" h z * *'
D(T—T') =<,&X(T) Ax(T') >= J | Dtl ^:<cpi(fi)cpi(f;)>, (9)
О о
где скобки <•••> означают усреднение по случайному ансамблю, который предполагается стационарным. С помощью (9) получаем коэффициент
Диффузии (см., например, [в])
1 г D(T) 1 1 / с г 7
D”=Tim. [—J-Т (я*л) (10)
О
Здесь DU 4. — коэффициент диффузии в рассматриваемых низкочастотных колебаниях, K(T) — нормированная корреляционная функция.
Если предположить, что К (T) имеет вид
K{t)=COS (щt ехр(—фf), (И)
То (10) совпадает с первым слагаемым в (7).
Таким образом, мы нашли, что сбой фазы колебаний приводит точно к такому же эффекту, что и диффузия ионов по ОУ в случае монохроматической волны. Но именно этого и следовало ожидать, поскольку в результате теплового движения ионов их Y-я координата, а вместе с ней и фаза колебаний для каждого отдельного иона меняются хаотически.
Рассмотрим теперь диффузию ионов в высокочастотных колебаниях Для этого представим У-Ю компоненту полного уравнения движения иона с учетом силы инерции в виде
* — (12)
Здесь Х=х+Уу/й){ — х-я координата центра ларморовского кружка, Y(t) — y-я координата иона, вращающегося по ларморовской окружности.
В случае низкочастотных колебаний коэффициент диффузии возрастает с уменьшением частоты. Это вполне понятно, так как при ю-*-0 увеличивается размах колебаний частицы по оси ОХ (см. (8)). Если рг*=0, то эффективная частота колебаний с w«d)< может также обратиться в нуль. (Под эффективной мы понимаем частоту, которую «видит» Отдельный ион.) В этом случае говорят о циклотронном резонансе. Как пояснено в [7], обращение эффективной частоты в нуль обусловлено доплеров - ским сдвигом, вызванным вращением частицы по ларморовской окружности. Для того чтобы выделить резонансную часть фи используем из
Вестное разложение плоской волны по цилиндрическим, вращающимся коаксиально с данным ионом:
Ов
Cos(wf—Куу)=* } /„(pA:j/)cos((ыi—гсФ*), (13)
Где р — расстояние от центра ларморовской окружности, Ф — азимутальный угол. Для данного иона р^р*, Ф*вФ(0)4-й)^. Если со«©*, Kvp{<Lt то, тсак следует из (13), резонансная часть потенциала равна: <pir>= ecpifc,,p/2Xcost—Ф(0) + ((!)—a>i)f]. Поскольку соударения хаотически меняют фазу ларморовского вращения, то движение ионов под действием колебаний с со«©* будет таким же, как и в случайном электрическом поле, нормированная корреляционная функция которого имеет вид
/T(f)=COS((d)—<Oi)f)exp(—^ViO - (14)
Уравнение (12) вполне аналогично (8), поэтому, повторяя вычисления, проведенные выше, и усредняя результат по ионному распределению, получим второе слагаемое в (7).
Проведенный анализ показывает, что в столкновительной неоднородной плазме диффузия может возникать даже в том случае, если колебания строго регулярны (см. также [*]).
Направленное движение ионов, рассмотренное в предыдущем разделе, является результатом их случайных блужданий и возникает лишь при наличии градиента плотности. Однако в выражении для потока (5) имеется также слагаемое, не зависящее от й)**<»х<. Следовательно, скорость ■отдельных ионов наряду с колебательной и хаотической составляющими должна включать также и составляющую, не зависящую от времени. Это означает, что при наличии столкновений волна должна заставлять ионы двигаться в определенном направлении (увлекать их). Для того чтобы выяснить, как возникает эффект увлечения, рассмотрим движение ионоа в гидродинамическом приближении (плотность плазмы, усредненную по колебаниям, будем считать не зависящей от координат):
TOC o "1-5" h z £1 + (УУ)У-и1[УЬ]-у1У - —уф1, (15)
1 Т
— +^(яУ)- 0, (16)
01
Где Ь — единичный вектор, параллельный 02.
В первом приближении по ф! из (15), (16) получаем
УХ1=А зт (а)1—ку)+В соз(й)^—Ку), (17)
V,,- —?•„ + —V«, (18)
(|>| <Й(
П,—п. — У, и (19)
0)
(й)2-у,2-й)*2)й),2 С 2vi(^)
Где А—------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------ Ку — ©«, В = - - - А.
Д (со2—V*2—со,2) 4-4у<2й)2 *Н*' 0)2-^2-0>42
Во втором приближении находим следующее выражение для средней по времени скорости движения ионов
1 Ку / Кусу1 *2
Вычислим теперь полный поток ионов по ОХ:
_1 Ку (1)1*+у<*+й)2 г*©** / КуС^ 2
” 2 0) 0);2+у,2 (о)ЛЬ,2-а>2)2+4гЛ)2 Н / *
Нетрудно найти, что при х,=0, 7=0 выражение (5) совпадает с (21).
Учитывая направление осей в используемой нами системе координат, находим, что ионы будут выноситься по радиусу наружу, если колебания бегут по азимуту в электронную сторону, т. е. в положительном направлении по оси ОУ((й/ку>0).
2. Амбиполярное электрическое поле
Дополнительный поток электронов, вызываемый колебаниями, можно вычислить в гидродинамическом приближении, так как частота колебаний мала по сравнению с электронной циклотронной, а ларморовский радиус электронов — по сравнению с длиной волны. Предполагая электронную компоненту изотермической, будем использовать уравнение непрерывности и уравнение движения. В последнем, в отличие от (15), учтем силу давления, но опустим силу инерции:
0=—r. Vrc+n^eVcp—о)Д Vh] —Vv,). (22)
Как известно, несмотря на малое значение продольного волнового числа (кх<.ку)у движение электронов вдоль магнитного поля играет важную роль в динамике дрейфовых колебаний. Поэтому следует включить в рассмотрение и z-ю компоненту уравнения движения. Рассмотрение, аналогичное проведенному в разделе 26, дает:
6А.=-.(<■>+<■>.•), (23>
ОЛ i, СО, О, +(|)е
СТ
Где Цe=Dekx2+Dej_kv2y D'=T'/mevey Ац_=£.( v./co*)2, со/ = —7~kvytej
Еп
£ с£фо
Х.=х — — --—.. В (23) часть 6/,х, пропорциональная дрейфовой частото 1 в ах
Со.*, дает диффузионный поток, а пропорциональная со обязана эффекту увлечения.
Электрическое поле находилось из условия равенства потоков:
(24)
Где Ыш определяется (23), 6/fa — (5), а потоки частиц, не связанные с колебаниями, как известно, даются выражениями
Dito <2ф0
IJ*33 D±i з' * Ojj-———та0= Djj7i0Xj, (25)
Ах ах
Где /=£, Ц Ь^=е^]/ ШзСОД Обратим внимание на то обстоятельство, что в выражения для потоков /*, б/* входит не градиент плотности DnJdx^y, nйr
(1т1о ^ С? ф0
А его превышение над равновесным х, тг0 -------------------- 4- —---- —- П0.
Dx Т1 <1х
В незамагниченной плазме электронный коэффициент диффузии (подвижности) намного превышает ионный, поэтому при отсутствии колебаний электрическое поле определяется из условия /„«о, откуда следует EdчJdx&y. Te. Интересно отметить, что в другом предельном случае хорошо замагниченной плазмы (со*>у<) в результате воздействия неустойчивых колебаний электрическое поле может достигнуть той же величины при обратном направлении ес&рхГ,. Действительно, известно [5]г что при со<^* в плазме газового разряда возбуждаются лишь дрейфовые колебания с частотой со«— (сТв/еН)кук (со<со„ /г,,р,<1). В этом случае дополнительный поток ионов, вызванный колебаниями, дается выражением
1 TOC o "1-5" h z Ку /с 2
----------- (со—со**) ( — Луф1) . (26)
2 со со* Н /
Если амплитуда колебаний достаточно велика, то выполняется условие |б/**|»|/<*|. Поскольку к тому же отдельные слагаемые В (26) намного превышают б/,*, то стационарное электрическое поле следует определять из уравнения б/^О. Используя выражение для частоты дрейфовых колебаний, получаем EdyJdxя^—y.(Tв+Ti). Поскольку обычно В Газовом разряде Те">Ти то имеем Ed^0/dx^—y. Te. Отметим, что именно такое поле, как правило, и наблюдается в неустойчивой плазме при (см., на
Пример, [*], а также ниже).
1. Экспериментальная установка и методика измерений
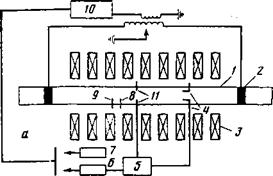
 Экспериментальное изучение стационарного электрического поля и влияние на него самопроизвольно возникающих в замагниченной плазме колебаний проводилось на установке, схема которой изображена на рис. 1. Слабоионизованная плазма создавалась в стеклянной трубке 1 длиной 1400 и диаметром 30 Мм при помощи ВЧ-генератора мощностью 400 Вт На частоте 6,4 Мгц. Трубка наполнялась аргоном при давлениях (Зн-20) • 10~3 Мм рт. ст., концентрация заряженных частиц не превышала
Экспериментальное изучение стационарного электрического поля и влияние на него самопроизвольно возникающих в замагниченной плазме колебаний проводилось на установке, схема которой изображена на рис. 1. Слабоионизованная плазма создавалась в стеклянной трубке 1 длиной 1400 и диаметром 30 Мм при помощи ВЧ-генератора мощностью 400 Вт На частоте 6,4 Мгц. Трубка наполнялась аргоном при давлениях (Зн-20) • 10~3 Мм рт. ст., концентрация заряженных частиц не превышала
|
|
|
Рис. 1. А - схема экспериментальной установки: 1 - разрядная трубка, 2 - латунные электроды, 3 - многосекционный соленоид, 4-12 Управляющих зондов, 5 - система обратных связей, 6 - селективный усилитель У2-&, 7 - генератор синусоидальных сигналов Г4-117, 8 - зонды для измерения радиального электрического поля, 9 — Зонды для измерения параметров флуктуаций плавающего потенциала, 10— ВЧ-ге - нератор, 11 - 12 приемных зондов системы обратных связей; Б - поперечное сечение разрядной трубки |
5*10* См~3. Разрядная трубка располагалась строго вдоль оси многосекционного соленоида 5, позволяющего получать однородное магнитное поле величиной до 2,5 Кэ на длине до 1 М.
Величина радиального электрического поля оценивалась с помощью двух цилиндрических зондов 5, отстоящих друг от друга на расстоянии
5 Мм, ориентированных перпендикулярно магнитному полю и смещенных относительно оси трубки так, что ось системы зондов располагалась между центром трубки и ее стенкой (см. рис. 1, Б). Зонды 8, подключенные к вольтметру с большим входным сопротивлением, позволяли определять разность потенциалов между фиксированными точками плазмы. Как известно, наличие в плазме ВЧ-напряжения приводит к искажению зондовой характеристики за счет эффекта «выпрямления» на нелинейности зондового слоя. Это приводит к тому, что разность между потенциалам пространства ср0 в данной точке и плавающим потенциалом зонда ср, оказывается зависящей от ВЧ-напряжения на зонде относительно плазмы. Для уменьшения влияния этого эффекта на точность измерения Ет по разности плавающих потенциалов были приняты следующие меры. Во-первых, зонды располагались в непосредственной близости от середины трубки и проводился контроль симметричности запитки разряда ВЧ-напряжением; в силу этого ВЧ-потенциал плазмы рядом с зондамп был минимален. Во-вторых, сопротивление зондовой цепи было порядка 30 Мом, что много больше дифференциального сопротивления призондо - вых слоев; таким образом, зондовый ток определялся не нелинейной проводимостью слоя, а активным сопротивлением зондовой цепи. В-третьих, разность фо—tpy зависит от но, как показали измерения, проведенные при помощи подвижных зондов, температура электронов практически не зависит от радпуса в исследуемых условиях. Все это позволило измерять Ет по разностп плавающих потенциалов двух зондов.
Для определения величины и спектра флуктуаций неустойчивой плазмы, а также для получения корреляционных характеристик использовались зонды 9, смещенные на расстояние 7 Мм от оси трубки и разнесенные в азимутальном направлении на 5 Мм друг от друга. Диаметр этих зондов ОД Мм, длина активной части 1 Мм. Сигналы, вызванные флуктуациями плавающего потенциала, с зондов 9 поступали на усилители У2-6 через сопротивления порядка 10 Мом и далее на аналоговый коррелятор. Использование коррелятора позволяло измерять мощность неустойчивых колебаний, а также определять азимутальное волновое число.
Для изменения уровня флуктуаций неустойчивой плазмы нами использовались два различных способа: действие на плазму обратных связей и слабая модуляция высокочастотного напряжения, питающего разряд генератора. Первый способ применялся ранее в работе [•]. Для его осуществления трубка снабжалась 12 одинаковыми приемными зондами 11г Идентичными зондам 9. Они располагались в центральном сечении трубки равномерно по его периметру на том же удалении от оси плазмы, что и зонды 9. На расстоянии 20 См от них в другом сечении трубки располагались 12 управляющих зондов 4. Диаметр каждого из них 1 Мм, а длина активной части — 20 Мм. Эти зонды располагались также равномерно по периметру, но ориентировались вдоль магнитного поля и были удалены от оси трубки на 7 Мм. Преобразуя с помощью системы обратных связей [*] сигналы с приемных зондов и подавая их на управляющие зондыг можно было изменять уровень мощности трех низших мод регулярных неустойчивых колебаний. Эта же система позволяла нам определять и номер моды существующих в плазме колебаний. Получаемые в устройстве [*] промежуточные преобразованные сигналы, пропорциональные косинусной компоненте каждой моды, оказывались в условиях работы близкими к гармоническим. Эти сигналы и использовались нами для осуществления второго способа воздействия на уровень флуктуаций плазмы. Для этого сигналы, усиленные селективным усилителем У2-8, подавались на модулятор ВЧ-генератора и вызывали модуляцию выходного напряжения, питающего разряд. В последнем случае управляющие зонды в системе обратных связей были отключены. Заметим, что иногда для модуляции напряжения нами использовался также низкочастотный генератор синусоидальных сигналов Г4-117 (см. рис. 1).
2. Экспериментальные результаты и их обсуждение
Опыты показали, что описанный выше способ управления с помощью обратных связей позволяет уменьшать амплитуду регулярных колебаний, которые в условиях опытов имели азимутальные волновые числа Т=2 и 3. Однако хотя амплитуда могла уменьшаться в 2 и даже в 3 раза, уменьшение стационарного радиального электрического поля ЕГ не превышало 5% 4. Такое незначительное изменение величины Ег, по-видимому, можно объяснить тем обстоятельством, что одновременно с ослаблением амплитуды регулярных колебаний в плазме наблюдалось увеличение уровня шумов. Вместе с тем в ряде случаев действие обратных связей приводило к увеличению амплитуды регулярных колебаний, что сопровождалось ростом значения |£г|. Это указывает на наличие срязи радиального электрического поля и уровня неустойчивых колебании плазмы. Отметим, что используемый метод оказывает воздействие на параметры плазмы, лишь влпяя на уровень неустойчивых колебаний.
Значительно большего изменения радиального электпического поля (на 30 % и более) удалось получить при модуляции питающего разряд ВЧ-напряжения. При этом одновременно с существенным уменьшением величины ЕГ в плазме, как показали корреляционные измерения, обна -
1 Здесь и в дальнейшем мы отождествляем Er с —Dyo/Dx (см. выше).
Руживается возбуждение волн с азимутальной модой тл=2, распространяющихся в направлении вращения положительных ионов в магнитном поле.
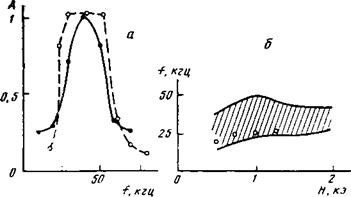
Искусственное возбуждение волн происходит лишь в определенной области частот и носит резонансный характер. Это хорошо видно из данных, приведенных на рис. 2,а, где показана зависимость амплитуды воз* буждаемых колебаний от частоты внешнего воздействия на плазму. Точками на рисунке обозначены результаты, полученные при модуляции ВЧ-напряжения синусоидальным сигналом независимого генератора 7 (см. рис. 1, А) при постоянной величине модуляции. Светлыми точками на
|
Рис. 2. а — резонансная кривая возбуждения искусственных волн; Л — амплитуда колебаний в произвольных единицах. Светлые точки - возбуждение сигналами обратных связей, темные точки — возбуждение независимым генератором. Давление газа р=10~2 Мм рт. ст., магнитное поле #=1000 Э (глубина модуляции 6%); Б - Область возбуждения искусственных волн в координатах / Н 0>»10~2 Мм рт. ст.). Точки - зависимость частоты, низкочастотных дрейфовых волн от Я (р=10"г Мм Рт. ст.) |
Рис. 2, А отмечены амплитуды волн в том случае, когда модуляция высокочастотного напряжения осуществлялась не независимым генератором, а сигналами с системы обратных связей, подаваемыми через селективный усилитель 6 при постоянном коэффициенте усиления. В этом случае управляющие зонды 4 были отключены (см. рис. 1 , а). Поскольку, как оказалось, второй способ воздействия на плазму позволял получать заданную амплитуду возбуждаемой волны при меньшей величине модуляции питающего разряд ВЧ-напряжения, то именно этот способ и использовался преимущественно в работе.
Дальнейшие опыты показали, что область частот искусственного возбуждения волн в плазме зависит от магнитного поля и давления газа. На рис. 2, б указана эта область частот при изменении магнитного поля от 0,5 до 2 Кэ. Заметим, что в условиях опытов одновременно с искусственно возбуждаемыми волнами наблюдались также самопроизвольно возникающие в плазме низкочастотные дрейфовые волны [3]. На рис. 2,6 точками показана зависимость их частоты от величины магнитного поля в отсутствие модуляции. Возбуждение волны при модуляции плазмы внутри резонансной области (см. рис. 2, а) сопровождается положительным приращением радиального электрического поля. При этом частота самопроизвольно возбуждающейся в плазме волны возрастает вследствие эффекта Доплера.
На рис. 3, а пунктирной линией показана рассчитанная по формулам (5), (23) —(25) зависимость величины отношения приращения стационарного радиального электрического поля АЕГ к квадрату амплитуды вызвавшей его волны ф4* от частоты этой волны /=<о/2я. При этом считалось, что возбужденная волна малой амплитуды монохроматична, ее азимутальное волновое число Т=2, а направление ее распространения совпа
Дает с направлением вращения положительных ионов в магнитном поле. Из рис. 3, а видно, что наиболее сильное влияние на радиальное электрическое поле должна оказывать волна на частоте 55 Кгц, близкой к ионной циклотронной частоте (максимум пунктирной кривой). При этом такая волна будет сообщать ионам направленное движение к центру плазмы. На том же рис. 3, А для сравнения точками нанесены результаты экспериментального определения зависимости АЕг/(р* от /, полученной с учетом
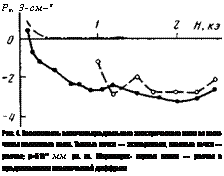
|
Рг, 3-см~г Рис. 4. Зависимость величины радиального электрического поля от величины магнитного поля. Темные точки — эксперимент, светлые точки — расчет; р=510”3 Мм рт. ст. Штрихпунк - тирная линия — расчет в предположении классической диффузии |
 Эффекта Доплера, который в этом случае оказывается значительным'. Как видно из рис. 3, а, экспериментальная зависимость также указывает на наличие резонанса при возбуждении волны. С увеличением давления газа резонансный характер поведения расчетных и экспериментальных кривых зависимости Д£г/ф12 от частоты / при частотах, близких к й),/2л, пропадает (см. рис. 3, Б). Последнее объясняется действием столкновений ионов с нейтральными атомами.
Эффекта Доплера, который в этом случае оказывается значительным'. Как видно из рис. 3, а, экспериментальная зависимость также указывает на наличие резонанса при возбуждении волны. С увеличением давления газа резонансный характер поведения расчетных и экспериментальных кривых зависимости Д£г/ф12 от частоты / при частотах, близких к й),/2л, пропадает (см. рис. 3, Б). Последнее объясняется действием столкновений ионов с нейтральными атомами.
Таким образом, полученные нами результаты показывают, что искусственное возбуждение волн в плазме* изменяющее спектр колебаний, изменяет и величину радиального электрического поля, причем это изменение согласуется с рассчитанным теоретически.
Представляет интерес установить, можно ли формулы (5), (23) —(25) использовать для определения величины радиального электрического поля в плазме в магнитном поле при самопроизвольно возникающих в ней неустойчивых колебаниях с известным спектром Частот и волновых чисел. В условиях проведенных опытов в плазме преобладали регулярные колебания, характеризующиеся одной частотой и одним волновым числом. Поэтому для расчета электрического поля Ет мы измеряли амплитуду, частоту и величину волнового вектора неустойчивых колебаний.
Рассчитанная таким образом зависимость Ег от Н с учетом эффекта Доплера при давлении 5-10"3 Мм рт. ст. изображена на рис. 4. Расчет удалось провести только для магнитных полей //>1000 Э. При этом в диапазоне изменения Н от 1000 до 1600 Э в плазме обнаруживались регулярные дрейфовые колебания с азимутальной модой т=2 и 3 при полях Н> >1600 Э. На том же рис. 4 точками изображена найденная на опыте зави-
•симость Ег от Н. Из рисунка видно, что теоретическая и экспериментальная зависимости находятся в удовлетворительном согласии. В соответствии с опытом расчет показывает, что радиальное электрическое поле в плазме направлено от стенки трубки к ее центру, а величина этого поля Ег~Тву./е (см. раздел И. З) в десятки раз превышает рассчитанную по классической теории парных столкновений.
При магнитных полях Я<1000 Э регулярные колебания в плазме не возбуждались, и спектр носил шумовой характер в широком диапазоне частот. В этом случае для расчета поля требуется учитывать уменьшение когерентности и длины корреляции шумовых сигналов, а также закон их дисперсии. Однако, полученные в работе экспериментальные результаты оказались недостаточными для проведения подобных расчетов.
Таким образом, в работе показано, что возбуждение неустойчивых колебаний в плазме влияет на величину радиального электрического поля Ег. Знание амплитудно-частотных характеристик колебаний и закона их дисперсии позволяет определить величину Ег. Рассчитанные значения радиального электрического поля для регулярных дрейфовых колебаний согласуются с найденными экспериментально.