Тиристорные электроприводы постоянного тока
Сравнение численных методов и метода линейных приближений
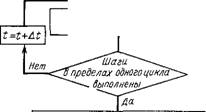
Более точных результатов при анализе поведения двигателя можно добиться применением численных методов решения дифференциальных уравнений (6.64) и (6.65) с помощью цифровой ЭВМ. При использовании численных методов решения справедливы для мгновенных значений тока и скорости, причем программа может отрабатывать любое изменение параметров, поэтому данные методы позволяют получить надежные результаты как при малых, так и при больших возмущениях. Алгоритм анализа приведен на рис. 6.14, а исходные уравнения имеют следующий вид:
Din _ ия Яя'я ^я, вгяш'—&остш _ J: (ф J. ^G GQ^
TOC o "1-3" h z Dt L„
= Кя ^1-Ва-МИ = F .j G Gl)
Dt J
|
(6.82) |
Данная система двух дифференциальных уравнений первого порядка может быть решена методом Рунге—Кутта [3]. Алгоритм на рис. 6.14 предусматривает анализ как установившихся, так и
Начало
Считывание Ванных-, параметры двигателя и сети, AMJf = 0,001 ,число шагов в цикле 36, предельное количество циклов 200, печать с интервалом 0,1с, начальные условия T(0), 1я(0),ш(0), угол управления ы:, момент нагрузки Мн
Запись начальных условий
Qt=0
|
Расчет с помощью метода Рунге - Кутта |
Считывание новых значений.
А и М,
|
Расчет среднего 1„ и среднеквадратичного 1Я кв токов, скорости ш, момента М, момента трения Всо |
|
Цикл— цикл+1 |
|
Печать конечных результатов |
|
Печать результатов |
|
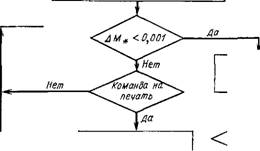
Рис. 6.14. Алгоритм расчета установившихся и переходных процессов в двигателе постоянного тока на цифровой ЭВМ |
|
Следующее^^да „возмущение^ нет Стоп |
Переходных режимов работы. Может исследоваться, в частности, переходный процесс пуска при нулевых начальных условиях. ^
Здесь проводится проверка адекватности линеаризованной в малых приращениях модели двигателя путем сравнения результатов анализа, полученных с ее помощью, с результатами численного анализа при аналогичных параметрах системы, задающих и возмущающих воздействиях. Ниже приведены временные зависимости для скорости и тока при ступенчатых воздействиях
Ш, рад/с — Численный метод - - Аинеаризобанная модель
|
О 0,4 0,8 1,2 1,6 2,0 2,4 T,C |
|
Рис. 6.16. |
|
1,0 2,0' Рис. 6.15. |
19,0 18,0
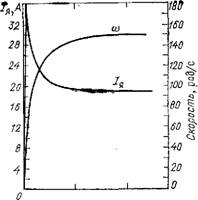
Рис. 6.15. Изменение скорости и тока двигателя последовательного возбуждения при пуске (численный метод)
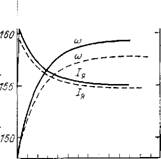
Рис. 6.16. Переходный процесс при изменении угла управления от 25° до О и питании двигателя постоянного тока последовательного возбуждения от однофазного полууправляемого преобразователя
По напряжению якоря и моменту нагрузки, полученные для линеаризованной «в малом» системы.
Ступенчатое изменение напряжения якоря. Решая (6.75) относительно Aco(s) и переходя к^оригиналу, получаем
Aco(s) = АС/я(5)йвШ/(1 + эт0) = kaaMJj[s( + эт0)]; (6.92)
Асо(0 = йцШД^/я(1-е-г/т°). (6.93)
Аналогично из (6.80)
AL(s) = Kal AUn(+ sxM)/[s(l + st0)]; (6.94)
A/fl(s) = ки1Шя [1/s —(т0 ^tm)/(1 + эт0)]; (6.95)
Д/я(0 = kaibUn [1 -(1 — тм/то)E~t/T" ] . (6.96)
Ступенчатое изменение момента нагрузки. Решив (6.86) относительно Aco(s) И перейдя к оригиналу, получим
(6.97)
(6.98)
Проведя аналогичные преобразования над (6.89), получим
|
Асо (S) = Kua AMH/[S (1 + St0)] ; Aco (T) = Kua AMH (1 — E~T/T°) . |
|
A-t/To |
|
(6.100) |
|
А/я (0 = kMMdH (l — |
|
Выводы. Анализ переходных процессов численным методом проведен в соответствии с алгоритмом, приведенным на рис. 6.14. |
А/я (s) = &мгДМн/[5(1 + это)]; (6.99)
Рис. 6.17. Переходный процесс при изменении момента нагрузки на 10 % и питании двигателя постоянного тока последовательного возбуждения от однофазного полууправляемого преобразователя
Графики изменения средних значений скорости и тока двигателя последовательного возбуждения при пуске с нулевыми начальными условиями представлены на рис. 6.15. Они иллюстрируют процесс пуска до достижения установившегося режима работы. Далее анализ отработки которых приво-
Происходят возмущения, дом проведен численным методом и путем решения линеаризованных уравнений (6.93), (6.96), (6.98) и (6.100). Сравнительные результаты при 5%-ном изменении напряжения якоря и 10 %-ном изменении момента нагрузки приведены на рис. 6.16 и 6.17. Параметры и коэффициенты уравнений даны в табл. 6.2.
Результаты, приведенные на рис. 6.16 и 6.17, свидетельствуют об удовлетворительной точности результатов анализа линеаризованной модели двигателя последовательного возбуждения.