ТЕОРИЯ сварочных процессов

Распределенные источники теплоты

В п. 6.4 отмечалось, что большинство сварочных источников теплоты, строго говоря, не сосредоточенные, а обладают распре­деленностью теплового потока по нормальному закону [уравне­ние (5.33)]. Если источник теплоты обладает высокой концент­рацией теплоты, то его можно рассматривать как сосредоточен­ный. Для некоторых источников теплоты, таких, как газовое пламя, а иногда и дуга, оказывается необходимым учет их рас­пределенности.

Ниже рассматривается только случай распределения теплоты по нормальному закону.

МГНОВЕННЫЙ НОРМАЛЬНО круговой источник

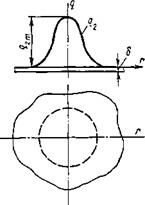
Определим приращения температуры в тонкой пластине в мо­мент введения теплоты мгновенным нормально круговым источ­ником, который действовал в течение времени dt (рис. 6.22). Количество теплоты на единицу поверхности пластины составит dT. Так как пластина тонкая, теплота мгновенно распространится равномерно по толщине б и нагреет ее на

dT — q2dt/(cp&). (6.65)

Подставив значение q2 из уравнения (5.33), получим

dT = _2!2ле_*,. (6 66)

Срб v

Оказывается, что распределение температуры в пластине ста­новится таким же спустя некоторое время to после введения теп­лоты мгновенным линейным источником:

dT _ _jdQ/S е-,»/(4ам /6 67)

cp(Anato)

Приравнивая показатели степеней в формулах (6.66) и (6.67), находим, что

f0=l/(4eJfe). (6.68)

Приравнивая первые сомножители формул (6.66) и (6.67), после преоб­разования получаем

dQ — qdt, (6.69)

т. е. мгновенное количество теплоты dQ сосредоточенного источника равно количеству теплоты, вводимой нор­мально круговым источником за время dt.

Таким образом, мгновенный распре­деленный источник теплоты можно за­менить сосредоточенным линейным ис­точником, теплота которого введена на отрезок времени to ранее. Согласно уравнению (6.6) процесс распростране­ния теплоты от мгновенного распределенного источника с уче­том to выразится уравнением

где t — время, прошедшее с момента введения теплоты нормально кругового источника.

С учетом теплоотдачи, которая происходит в течение времени t,

dT = ____ ^___ е-<-г/На(( + („)]-6((+Ь)еЫ„ (6.71)

cpfi4ita(/+4) ' '

Если теплота нормально кругового источника введена на поверхности полубесконечного тела, а затем распространяется по нему, то этот процесс формально можно представить как процесс распространения теплоты от мгновенного точечного ис­точника теплоты на поверхности полубесконечного тела с тем, однако, условием, что теплота в течение времени to распростра­няется только по поверхности тела, а затем продолжает распро­страняться и по поверхности, и в глубину в направлении оси OZ. Такой процесс выражается следующим уравнением:

JJ - 2gdt е— '■2/14а(<+<о)1 £—zV(4af)

ср 4ла(і+(0) (4nat)w‘2'

ДВИЖУЩИЙСЯ НОРМАЛЬНО КРУГОВОЙ источник

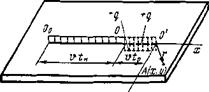
Процесс нагрева пластины движущимся нормально круговым источником рассматривается с использованием принципа нало­жения (рис. 6.23), аналогично тому, как это было сделано в п. 6.2 Для линейного источника теплоты. Допустим, что ИСТОЧНИК тепло­
ты вышел ИЗ ТОЧКИ О О и про­двинулся в точку О. Требуется определить приращение темпе­ратуры в точке А. Чтобы учесть распределенность источ­ника теплоты, необходимо предположить, что теплота в точке О выделилась на t0 се­кунд ранее. Формально это можно представить так, что вместо реального распределен­ного источника теплоты дви­жется некоторый фиктивный сосредоточенный источник теплоты с опережением во времени на to и по расстоянию на vt0. Этот фиктивный источник теплоты находится в точке О'. Очевидно, что на участке ОО' никакой теплоты не выделялось; поэтому необходимо ввести сосредоточенный фиктивный сток теплоты той же мощности, который действовал только на отрезке ОО'.

Располагая для удобства подвижную систему координат в точке О', по аналогии с уравнением (6.25) и с учетом выражения (6.71), запишем

*н"Мо

ду - _________ Ч, — ох/(2а)+ЬЬ f e-{v2/(4a)+bt-r2/(4at) jli __________

4яЯ,6 ^ t

t«

— - JL_p —«/(2n) + fti„ [ e _[ u7(4a)+61f-r;/(4ab dt (6.73)

4лХб J t

Уравнение (6.73) выражает стадию теплонасыщения. Числен­ное определение приращений температуры по уравнению (6.73) может быть выполнено с использованием коэффициента тепло­насыщения (см. рис. 6.11, б):

АТ = АГпре*'°[ф2(р2; т„ + то) — ф2(р2; т0)], (6.74)

где

tir-і/ , , Aba v2L (, . Aba .

p*= 27V 1 + - p-; =

v2t( . і 46a

T0 = laV + ^r)-

В предельном состоянии при tH ОО

АТ = АТпреь‘0[ 1 — ф2(рг; т0)]. (6.75)

Значение А7„р находят по формуле (6.26).

Формулы, описывающие нагрев полубесконечного тела дви­жущимся нормально круговым источником теплоты, а также на­грев пластины и массивного тела мощными быстродвижущимися
распределенными источниками теплоты, можно найти в работе [22].