Нагрев тел вращения
ТОНКОСТЕННЫЙ ЦИЛИНДР
Нагрев при однопроходной дуговой сварке продольных и кольцевых швов тонкостенных цилиндрических оболочек, несмотря на их кривизну, может быть приравнен к случаю нагрева пластины линейным источником теплоты. Это объясняется тем, что цилиндр представляет собой развертывающуся поверхность.
При больших размерах цилиндра (диаметр и длина) процесс распространения теплоты аналогичен процессу в бесконечной пластине. Однако при малых диаметрах происходит наложение тепловых потоков от различных участков выполняемого шва. Рассмотрим общий случай нагрева тонкостенного цилиндра источником, который начинает свое движение из точки О (рис. 6.19, а) под некоторым углом а к образующей цилиндра достаточно большой длины. Процесс распространения теплоты в цилиндре диаметром d в этом случае аналогичен случаю одновременного движения бесконечно большого числа источников теплоты из точек 0, О2, ..., On, сдвинутых относительно друг друга на шаг лd (рис. 6.19,6). Температурное поле достаточно рассматривать в пределах одного интервала nd, так как оно будет повторяться во всех других интервалах.
Если угол а равен 90°, то это соответствует случаю сварки кольцевого шва. Иногда при сварке кольцевых швов тонких оболочек делают второй, третий и последующие проходы без остановки — либо с целью заполнения разделки шва, либо с целью выполнения так называемой автоопрессовки (для получения увеличенной поперечной усадки кольцевого шва). В этом случае источники теплоты, вышедшие ИЗ О2...О4 и т. д., перекрывают точку О, откуда начал движение «основной» источник, который играет роль источника теплоты первого прохода.
Если а= 0, то это соответствует сварке продольного шва. Наличие множества параллельно движущихся источников в расчетной модели для этого случая предназначено для учета отражения теплоты от сечения, диаметрально противоположного образующей, где выполняется продольный шов.
Случай 0 < а < 90° соответствует сварке спирального шва или наплавке по винтовой линии.
Для упрощения расчетов источник теплоты иногда считают быстродвижущимся. При сварке кольцевого шва эта схема предусматривает распространение теплоты, выделившейся на участке dS (рис. 6.19, в), только в плоскости /—/. При многократном
|
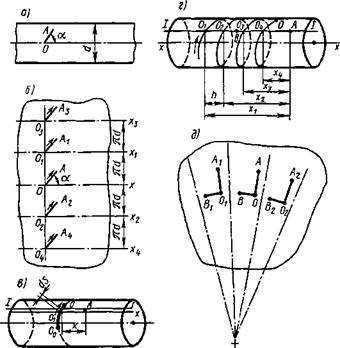
Рис. 6.19. Схемы тел и движения линейных источников теплоты при нагреве тонкостенных тел вращения: |
о — тонкостенный цилиндр; б — эквивалентная схема для тонкостенного цилиндра; в — быстродвижущийся источник в цилиндре, г — движение источника по винтовой линии; д — эквивалентная схема для тонкостенного конуса
пересечении источником теплоты плоскости 1—1 приращения температурных полей от отдельных источников суммируются. Например, для определения приращения температуры в точке А по аналогии с формулой (6.45)
ДГ =2 --------- 9------------------- , (6.55)
« vb -j4nXcpta
где п — число пересечений источником теплоты плоскости /—/, в которой находится точка А tn — время, прошедшее с момента пересечения источником плоскости 1-І при первом, втором и т. д. проходах (нумерация проходов ведется от первого прохода, т. е. время tn уменьшается по мере увеличения индекса «/г»).
Например, если источник теплоты на рис. 6.19, в совершает четвертый оборот, выйдя из точки О о, и находится в точке О, при этом время одного оборота равно 10 с, а время прохождения отрезка ОіО равно 2 с, то п = 4; t = 3-10 + 2 = 32 с; t2 = = 2-10 + 2 = 22 с; h = 1 • 10 + 2 = 12 с; U = 2 с.
При винтовой наплавке на тонкостенный цилиндр (рис. 6.19,г) можно также приближенно пользоваться схемой быстродвижу - щегося линейного источника теплоты в пластине с суммированием температурных полей от отдельных источников. Если приближенно полагать а » 90°, то
АТ =2 --------------------------------------------- (6.56)
п об V 4лЯсо/л
где п — число пересечений источником теплоты плоскости /— /, в которой находится точка А (см. рис. 6.19, г); х„ — расстояние до точки А в плоскости /—I при различных проходах, т. е. Х, Х2, ..., хп tn — время, прошедшее с момента пересечения источником теплоты плоскости /—/ при первом, втором и т. д. проходах (нумерация проходов ведется от первого).
Для точки В на рис. 6.19, г периоды времени t, t2, h, ti и т. д. те же, что и для точки А, так как точка В находится в одной плоскости с точкой А, на координаты х, х2, Хз и т. д. будут иметь другие значения.
ТОНКОСТЕННЫЙ КОНУС
При расчетах температурных полей в случае выполнения продольного шва на конусе небольшого диаметра необходимо принимать во внимание, что конус развертывается в клиновидную пластину. Тогда температурное поле при выполнении продольного шва будет таким же, как при одновременном движении ряда источников из точек О, О і, О 2 и т. д. в радиальном направлении (рис. 6.19, (?) по прямым линиям ОА, 0А, 02А2. Сварка кольцевого шва на конусе соответствует движению ряда источников по дугам окружности OB, 0Ві, 02В2 и т. д.
Распространение теплоты при сварке экваториальных однопроходных швов на тонкостенных сферах происходит при некотором стеснении теплового потока вследствие кривизны сферы в двух направлениях. Температура точек оказывается несколько выше, чем в бесконечной пластине той же толщины. На сферах большого диаметра с малой толщиной стенки этим влиянием можно пренебречь, если
<200, (6.57)
vcp8Rc
где Rc — радиус сферы.
СПЛОШНОЙ КРУГЛЫЙ ЦИЛИНДР
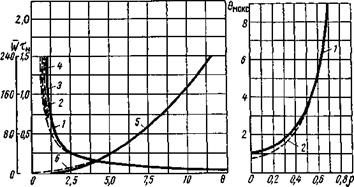
Температурное поле при движении точечного источника теплоты по поверхности сплошного цилиндра описывается сложными зависимостями. Формулы оказываются проще, если исходить из предположения, что источник теплоты быстродвижущийся. Тогда при наплавке по образующей цилиндра процесс распространения теплоты можно представить как выравнивание температур от мгновенного источника Q, расположенного в точке <р = 0 тонкого диска радиусом го, торцы которого теплоизолированы, а теплота отдается лишь с цилиндрической поверхности (рис. 6.20, а). В этом случае результаты подсчетов для точек по линии наплавки (г = г0, ф = 0) представлены на рис. 6.21, а, где
Q _ (7—T»)3rj£2— безразмерная температура; w = — X
4
лгоср относительная мгновенная скорость охлаждения по ли-
(q/v)a v
нии наплавки в момент, когда температура точки равна Т тн = безразмерное время пребывания точки, находящейся
г о
на линии наплавки выше некоторой температуры 0 — время,
с, пребывания точки, находящейся на линии наплавки выше не
которой температуры Т) Ти — начальная температура тела.
|
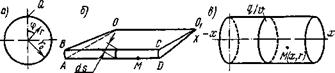
Рис. 6.20. Различные схемы движения и расположения источников теплоты при нагреве сплошного круглого цилиндра |
На рис. 6.21, б представлены максимальные относительные температуры
О ^ (7щах Тн) ЛГоф '-'max. >
где Гтах — максимальная температура в рассматриваемой точке, достигаемая при распространении теплоты в цилиндре.
Кривые на рис. 6.21, о, б построены для различных значений безразмерного критерия аго/Х, характеризующего теплоотдачу с поверхности.
Наплавку на сплошной цилиндр по винтовой линии малого шага с некоторыми допущениями можно рассматривать как
|
|
|
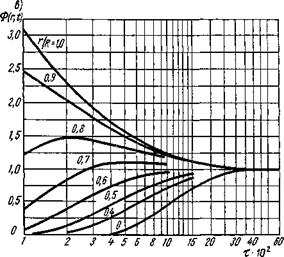
Рис. 6.21. Безразмерные характеристики температурного режима в зоне наплавки длинного сплошного круглого цилиндра: а — безразмерное время тн пребывания точек выше относительной температуры 0 при наплавке вдоль образующей (/ — аго/А = 0,2 — 0,04, 3 — 0,1, 4 — 0,15) н относительная мгновенная скорость охлаждения w по линии наплавки (5 — аго/А = 0, 6 — 0,15); б — максимальные относительные температуры 0макс при наплавке вдоль образующей в зависимости от относительной координаты р2 = г/го при ср = 0: (/ — аго/А = 0, 2 — 0,15); в — номограмма для определения функции Ф(г, t) |
О) б)
нагрев сплошного цилиндра быстродвижущимся точечным источником теплоты, перемещающимся по поверхности цилиндра. Допущение о том, что источник быстродвижущийся, по существу означает, что теплота, выделившись на линии dS (см. рис. 6.20, б), распространяется только в клине, ограниченном двумя не пропускающими теплоту плоскостями, проходящими через ось цилиндра, и цилиндрической поверхностью ABCD, с которой происходит теплоотдача. Так как обычно угол винтовой линии мал, распространение теплоты в этом случае может быть приравнено к случаю распространения теплоты от мгновенного кольцевого источника с погонной энергией q/v на поверхности сплошного цилиндра (см. рис. 6.20, в).
Приращение температуры точки М(х, г), если его определять от одного пересечения источником теплоты ПЛОСКОСТИ AOOD (см. рис. 6.20, б), в которой находится точка М(х, г), будет зависеть от времени t, прошедшего после пересечения ПЛОСКОСТИ, и не будет зависеть от координаты ф точки М. Приращение температуры в сплошном цилиндре при распространении теплоты от мгновенного кольцевого источника теплоты с учетом теплоотдачи можно определить по формуле
ДГ = -|^ф(г10-^^-, (6.58)
«Лер V ' -[4яаГ
9ґу
где Ь = t — время, прошедшее с момента выделения теплоты; R— наружный радиус цилиндра.
Функция Ф(г, t), входящая в формулу (6.58), выражает процесс выравнивания теплоты в тонком круглом диске без теплоотдачи, если теплота выделилась мгновенно по кольцу на наружной поверхности диска:
ф(r,0= £ My*r/R (6.59)
Я=1 МРк)
где рк—корни уравнения /і(рк) = 0 (щ = 0, р2 = 3,83, р3 = = 7,02 и т. д.); j0 и ji — функции Бесселя 1-го рода нулевого и первого порядков от действительного аргумента.
На рис. 6.21, в представлена номограмма для определения численных значений Ф(г, t) в зависимости от r/R и т = at/R2. При т > 0,4 значение Ф(г, t) да 1.
При движении источника теплоты на поверхности сплошного цилиндра по винтовой линии малого шага (см. рис. 6.19, г) приращение температуры точек А и В выразится как сумма приращения температур от мгновенных кольцевых источников, расположенных на различных расстояниях х от точек А и В и для которых время t, прошедшее с момента пересечения плоскости I — I движущимся источником теплоты, различно:
дт _ - Й-f Ф„(г, (6.60)
уЛсРя=1 у 4 natn
где хп — расстояния до точки А или В в плоскости 1-І при
различных проходах, т. е. при Х, xi, х3 и т. д.; tn — время, прошедшее с момента пересечения источником теплоты плоскости 1 — 1 при соответствующих проходах (нумерация проходов ведется от первого прохода); N— число проходов с начала наплавки.
Когда число проходов N велико, т. е. рассматривается установившийся процесс, определение приращения температуры АТ по формуле (6.60) затруднительно. В этом случае рекомендуется использовать следующий прием. Суммирование приращений температур по формуле (6.60) следует вести до такого значения л = . = N', когда Ф„(г, tn) заметно отличается от единицы (например, на 3—5%). При этом будет найдено значение ATNb. Остальную часть суммы уравнения (6.60) при n^>N', когда Ф„(г, tn) « 1, следует вычислить, используя интеграл
АТн-н-= - l-VxX/{2a) е-(»ї/(4<.Н*)*-И/(4вІіЛ, (6.61)
срдуїїш (tN,+ih/2)
где tN, — время, прошедшее с момента пересечения плоскости 1-І при проходе п = N' th — время, затрачиваемое на один проход с шагом h (см. рис. 6.19, г); Хо— координата точки А или В (см. рис. 6.19, г) по отношению к точке О, где находится движущийся источник теплоты; vx — составляющая скорости движения источника теплоты вдоль оси цилиндра х — х.
Интеграл (6.61) описывает процесс выравнивания температур от плоского источника теплоты [см. п. 6.3 и уравнение (6.29)], т. е.
^TN_N’= АГ^Ї фі),
где фі определяются по номограмме (см. рис. 6.11, в), a АТпр— по формуле (6.30).
При использовании формул (6.30) и (6.35) для данного конкретного случая в них следует принимать
Окончательно получим
АТ = A7V+ ATn_n.= A7V + АГпр(1 - ф,). (6.62)
ТОЛСТОСТЕННЫЙ ЦИЛИНДР
При наплавке на полый толстостенный цилиндр по винтовой линии малого шага также можно использовать схемы быстродви- жущегося источника теплоты. Принципиально ход рассуждений при выводе формул тот же самый, что и в случае сплошного цилиндра. Приращения температур определяют по формулам, структура которых аналогична структуре формул (6.60) и (6.62). Отличие заключается в том, что вместо функции Ф„(г, /„), выражающей выравнивание температур в сплошном тонком диске, в формулу входит функция Ф„(г, tn) [см. формулу (6.52) ], выра-
жающая процесс выравнивания температур в направлении толщины стенки трубы б:
АТ = - f-2 Fn(z, L) e-*2M-ht - . (6.63)
цвсРп=1 У4лаї„
Коэффициент температуроотдачи Ь вычисляют с учетом отдачи теплоты наружной и внутренней поверхностями трубы, причем в случае, если теплоотдача различна (например, охлаждение водой изнутри), значение b подсчитывают по формуле
b = (а, + а2)/(срб), (6.64)
где gsi и аг — коэффициенты теплоотдачи наружной и внутренней поверхностями трубы.
Последовательность операций при вычислении температур та же, что и в случае сплошного цилиндра.
Зависимости, описывающие более сложные процессы распространения теплоты в цилиндрах, имеются в работах [15].