СОВРЕМЕННЫЕ СИСТЕМЫ УПРАВЛЕНИЯ

Временные характеристики и переходная матрица состояния

Довольно часто возникает необходимость оценить изменение переменных состояния во времени и тем самым судить о качестве системы управления. Переходные характеристики системы легко можно получить путем решения уравнения состояния. В разд. 3.3 такое ре­шение было получено, и оно имеет вид:

і

х(/)=Ф(г)х(0)+ |ф(г-т)Ви(т)с/т. (3.72)

о

Если известны начальные условия х(0), вектор входных воздействий u(r) и переход­ная матрица состояния Ф(/), то реакция системы х(/) может быть вычислена тем или иным способом. Таким образом, задача сводится к вычислению матрицы Ф(/), которая в основ­ном и определяет реакцию системы. Один из способов вычисления переходной матрицы состояния базируется на использовании сигнального графа системы. Но, прежде чем рас­сматривать этот способ, следует упомянуть и некоторые другие методы, в частности вы­числение ряда

Ф(г) =exp(Ar) = (3-73)

*=о А!

с ограниченным числом членов. Известны также весьма эффективные методы вычисления Ф(/) с помощью компьютерных алгоритмов.

В уравнении (3.25) было показано, что Ф(л) = (si-А) 1. Тогда, если вычислить об­ратную матрицу, то мы сможем найти и Ф(/) как обратное преобразование Лапласа для Ф(л), т. е. Ф(/) = £_1[Ф(5)]. К сожалению, для систем высокого порядка операция нахожде­ния обратной матрицы является очень трудоемкой.

Преимущества сигнального графа при получении переходной матрицы состояния становятся очевидными, если рассмотреть преобразование Лапласа уравнения (3.72), счи­тая входные сигналы равными нулю. Тогда при и(т) = 0 из (3.72) мы имеем:

X(s) = 4>(s)x(0). (3.74)

Это означает, что мы можем определить преобразование Лапласа для переходной матрицы состояния по сигнальному графу, установив связь между переменной состояния X,(s) (в виде изображения по Лапласу) и начальными условиями [д^ (0), х2(0),..., *„(0)]. Тогда пере­ходная матрица состояния просто будет обратным преобразованием Лапласа от ®(s), т. е.

®W = r'[®(s)].

Зависимость переменной состояния X, (s) от начальных условий х(0) определяется с помощью уже известной нам формулы Мейсона по сигнальному графу. Так, для системы второго порядка мы получим:

(я) = Фі і (sK (0) + ф12 (s)x2 (0),

Х2 (s) = ф2, (s)x, (0) + ф22 (s)x2 (0> (3.76)

где связь между X2(s) их,(0) определяется с помощью формулы Мейсона по сигнальному графу. Все элементы переходной матрицы состояния, cpy(s), могут быть получены путем установления связи между X,(s) и х;(0) по структуре сигнального графа. Данный способ определения переходной матрицы состояния иллюстрирует следующий пример.

Пример 3.5. Вычисление переходной матрицы состояния

Рассмотрим RLC-цепь, изображенную на рис. 3.4, и вычислим Ф(г) двумя способами: (1) пу­тем нахождения обратной матрицы <P(s) = (si - А)~' и (2) с помощью формулы Мейсона по сигнальному графу.

Сначала воспользуемся первым способом. Из уравнения (3.18) нам известна матрица А:

'0 -2 1 -3

А =

Тогда

2

(s+3)

Обратная матрица равна

где A(s) = s(s + 3) + 2 = s~ + 3s + 2 = (s + l)(s + 2).

Сигнальный граф для этой цепи был приведен на рис. 3.5, где в качестве переменных состоя­ния приняты *1 = vc и х2 = г'/. Начальные условия jcf(0) и л2(0) представляют собой соответст­венно начальное напряжение на конденсаторе и начальный ток через индуктивность. Сигналь­ный граф с учетом этих начальных условий изображен на рис. 3.20. Начальные условия учте­ны в виде начальных значений переменных состояния на выходе каждого интегратора.

Рис. 3.20

Сигнальный граф для Я/.С-цепи

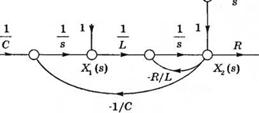
Для вычисления Ф(у) положим U(s) = 0. При R = 3, L - 1 и С = 1/2 сигнальный граф примет вид, изображенный на рис. 3.21. Входной и выходной узлы исключены, т. к. они не участвуют в вычислении Ф(ї). С помощью формулы Мейсона выразим зависимость Хх (у) отх^О):

х - ч _ 1-А|(у)-[х,(0)/у]

’ А(»)

где Д(у) — определитель графа, a A((s) — дополнительный множитель для пути. Определитель графа

Д(ї) = 1 + 3s“' + 2s“2,

а дополнительный множитель A|(s) = 1 + Зі”1, потому что путь отх,(0) kX|(j) не касается кон­тура с коэффициентом передачи —Зі"1. Таким образом, первый элемент переходной матрицы состояния равен

(1 + 3s-,)(1/j) s + 3

Фц(*) =

1 + 3s + 2 s

Элемент <p12(s) вычисляется как реакция A_,(s) на начальное условие jc2(0):

(-2*-')[д*(0Уа]

1 + 3s'1 + 2s~2 '

откуда

Характеристический полином s~ + 3s + 2 = (s + l)(s + 2), поэтому окончательно получим:

~(2е' - еъ) (~2е' + 2еъ)

(е' - е2') (-е-' + 2еъ) '

Реакцию RLC-иепч на различные начальные условия и входные сигналы можно получить с по­мощью выражения (3.72). Например, при Л|(0) = л:2(0) = 1 и u(t) = 0 мы имеем:

*|(0

*2(0

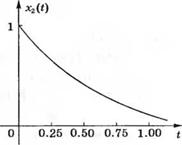
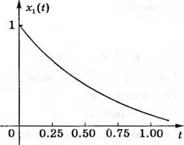
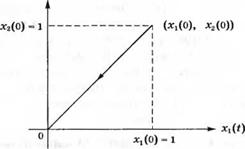
Реакция системы на эти начальные условия изображена на рис. 3.22. а на рис. 3.23 приведен го­дограф вектора состояния в координатах (x|s х2).

Определение временных характеристик системы, как мы видели, значительно упрощается в результате вычисления переходной матрицы состояния. Необходимо, однако, заметить, что применимость этого метода ограничена только классом линейных систем.