СОВРЕМЕННЫЕ СИСТЕМЫ УПРАВЛЕНИЯ
Возмущения в системах управления с обратной связью
Третьей важной функцией обратной связи в системах управления является частичная компенсация влияния возмущений. Возмущение — это нежелательный входной сигнал, который оказывает влияние на выходной сигнал системы. Многие системы управления подвержены влиянию внешних воздействий, приводящих к отклонению выходного сигнала от желаемого значения. Так, в электронных усилителях всегда имеет место шум, возникающий в транзисторах или интегральных схемах; на антенны радиолокаторов влияют порывы ветра; во многих системах также возникают искажения за счет присутствия в них нелинейных элементов. Системы с обратной связью обладают тем преимуществом, что в них влияние всех этих негативных факторов может быть существенно снижено.
В качестве примера системы с нежелательным возмущением рассмотрим уже знакомую нам систему управления скоростью вра - ^
|
© |
щения привода валков прокатного стана.
|
Стальная полоса -> "© |
|
Ь О ОХУОТЛТ |
Валки, через которые проходит стальная полоса, подвержены значительному изменению нагрузки, играющей роль возмущения.
|
Транспортер |
Пока стальная полоса приближается к валкам (см. рис. 4.10), они по существу вращаются без нагрузки. Однако когда полоса по - Рис. 4.10. Прокатный стан
падает между валками, то нагрузка на них
мгновенно становится значительной. Этот эффект может быть учтен в виде ступенчатого изменения возмущающего момента, как показано на рис. 4.11. Тот же эффект можно проиллюстрировать, используя нагрузочные (внешние) характеристики типичного электродвигателя, изображенные на рис. 4.12.
Возмущение
7»
|
1 |
Vs) |
Кт |
-X TL(s) |
1 |
|
|
к |
+ |
J'+Ъ |
|
ПротивоЭДС двигателя |
|
Ч(«) —iQ |
|
. co(s) Скорость |
|
К, |
|
Момент нагрузки (Н • м) |
Рис. 4.11. Разомкнутая система управления скоростью (без главной обратной связи)
Рис. 4.12
Нагрузочные характеристики двигателя
Для двигателя постоянного тока, управляемого по цепи якоря, в примере 2.4 была получена модель в виде структурной схемы. Эта модель воспроизведена на рис. 4.11, причем предполагается, что La~ 0. Ошибка системы на рис. 4.11 равна
E(s) = R(s) - to(,v),
где R(s) = соJ(s) есть желаемое значение скорости. Для упрощения вычислений положим R(s) = 0 и будем исследовать £(,v) = - to(,v), т. е. изменение скорости, вызванное возмущением:
1
|
Td(s). |
|
(4.35) |
£(s) = - co(s) =
Js + b + KmKb/Rt
При ступенчатом изменении момента нагрузки T^s) = D/s, и с помощью теоремы о конечном значении мы можем определить установившуюся ошибку:
lim e(t) = lim E(s)= lim, v-------------- ?---------------- — = —------------ =-co0(co)----- (4.36)
|
b + KmKb/Ra |
|
A'-»0 |
Js + b + К mK ь / Ra
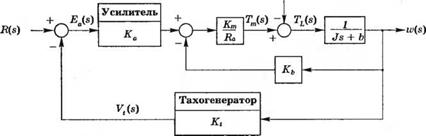
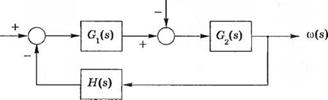
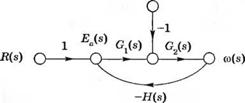
Замкнутая система управления скоростью в виде структурной схемы изображена на рис. 4.13. Та же система, но в виде сигнального графа, изображена на рис. 4.14, где G^s) = KJCJRa, G2(s) = 1 /(Js + b) и H{s) = K, + Kb /Ки. По сигнальному графу с помошью формулы Мейсона можно получить выражение для ошибки E(s) = - to(,v):
G2(s)
|
(4.37) |
|
■TAs). |
£(s) = - co(s) = -
l + G,(i)G,(5)ff(s)
Если в некотором диапазоне комплексной переменной s выполняется условие GG2H(s) » 1, то можно считать, что
Д(д)я^,!„,ч-Г'(д)- (4-38>
G, (s)H(s)
Следовательно, если произведение Gx(s)H(s) сделать достаточно большим, то влияние возмущения можно существенно уменьшить. Заметим, что
кАкак„к,
|
К, + |
|
R., |
Gx(sms)=K°Km
R„
поскольку Ка » Кь. Поэтому мы должны постараться получить большой коэффициент усиления Ка и сохранить Ra< 2 Ом. В системе на рис. 4.14 ошибка E{s) = R{s) - to(,v), где R(s) = соJ(s) есть желаемое значение скорости. Как и в разомкнутой системе, положим R(s) = 0 и исследуем со(л).
r„<*)
|
|
Рис. 4.14
|
ТЛв) |
|
а) |
|
|
Замкнутая
система
управления
скоростью.
(а) Модель в виде структурной схемы.
(б) Модель
в виде графа
|
б) |
ад
|
|
Выражение для выходной переменной системы на рис. 4.13 при R(s) = 0 можно получить с помощью формулы Мейсона:
|
ф) = |
-1 /(Js+b)
TAs) =
1 +(K, KaKm/Ra )[1/(Л+ Ь)] + {KaKb/Ra)[V{Js+b)] 1 T,(s).
(4.39)
Js + b + (К m / Ra )(K, Ka +Kb ) По теореме о конечном значении находим:
1
|
■D: |
|
(4.40) |
lim со(/) = lim, vto(.s') =
I —>00 Л—>0
b + (Km/Ra )(K, Ka +Kb) если коэффициент усиления Ka достаточно велик, то
ш(оо)« —---------------------------------------------- £)- = со (да). (4.41)
F F F
Сравнивая изменение скорости из-за нежелательного возмущения в замкнутой и разомкнутой системах, получим:
|
(4.42) |
|
О 3 |
300 |
|
& Л |
200 |
|
о о Рн |
100 |
|
Й О |
|
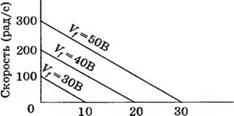
1^=50 В vi =40 В Vf= ЗОВ |
|
и 10 20 30 Момент нагрузки (Н - м) Рис. 4.15. Нагрузочные характеристики замкнутой системы |
|
со0(«0 KaKmK, Обычно это отношение не превышает 0,02. Преимущество замкнутой системы |
|
соДсо) Rab + KmKt |
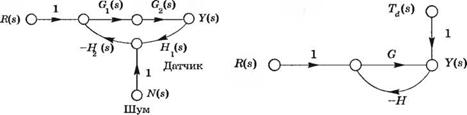
Основная причина введения обратной связи состоит в ее способности уменьшать влияние внешних возмущений и шумов, возникающих внутри системы. Во многих системах шум возникает на выходе измерительного элемента (датчика). Этот шум можно представить в виде сигнала N(s), как показано на рис. 4.16. Влияние шума на выходную переменную оценивается выражением
-GxG2H2(s)
|
(4.43) |
Y (s) =
l + GxG2HxH2(s)
или, приближенно,
1
|
(4.44) |
|
• A'(.v). |
r(s)«-
Я, (s)
Очевидно, что проектировщик должен стремиться получить как можно большее значение Hx(s), что эквивалентно максимизации отношения сигнал/шум на выходе датчика. Кроме того, элементы обратной связи H(s) должны работать при минимальном шуме, дрейфе и изменении параметров. Это требование вытекает из функции чувствительности (4.13), которая показывает, что Sjj ~ 1 Следовательно, необходимо принять все меры, чтобы датчик и элементы обратной связи обладали стабильными характеристиками. Как правило, этого всегда удается добиться, т. к. элементы обратной связи работают при малом уровне мощности и с незначительными затратами могут быть изготовлены с высоким качеством.
Эквивалентность чувствительности Sq и реакции замкнутой системы на внешнее возмущение можно проиллюстрировать с помощью рис. 4.14. Чувствительность системы к изменению G2 равна
(4.45)
|
1 |
1
2 1 + GxG2H(s) GxG2H(s)
Влияние возмущения на выходную переменную при R(s) = 0 оценивается выражением
Ж =_________________________ 1— (4.46)
Td(s) l + GxG2H(s) GxH(s)
В обоих случаях мы видим, что нежелательные эффекты можно ослабить путем увеличения коэффициента Ка, входящего в (7,(.?). Примечательно, что меры по уменьшению влияния изменения параметров системы или внешних возмущений эквивалентны и по счастливому стечению обстоятельств действуют одновременно. В качестве заключительной иллюстрации этого факта мы отметим, что для системы, изображенной на рис. 4.17, влияние шума или возмущения на выходную переменную оценивается выражением
Y (s) 1
(4.47)
Td(s) 1 + GH(s) что полностью совпадает с чувствительностью Si
|
|
|
Рис. 4.17. Замкнутая система управления при наличии шума на ее выходе |
|
Рис. 4.16. Замкнутая система управления при наличии шума датчика |
Очень часто шум присутствует во входном сигнале системы. Например, входной сигнал может иметь вид r(t) + n(t), где r(t) соответствует желаемому виду реакции системы, а n(t) — шум. В данном случае замкнутая система будет реагировать на шум точно так же, как и на сигнал r(t), и будет неспособна улучшить отношение сигнал/шум на входе. Однако, если частотные спектры полезного сигнала и шума на входе системы разнесены друг от друга, то можно добиться улучшения отношения сигнал/шум на выходе системы. Во многих случаях для этого достаточно, чтобы замкнутая система представляла собой фильтр низких частот.