СОВРЕМЕННЫЕ СИСТЕМЫ УПРАВЛЕНИЯ
Тестовые входные сигналы
Важнейший интерес при анализе качества представляет поведение систем управления во времени, т. к. эти системы объективно являются динамическими. Прежде всего необходимо определить, устойчива ли система управления (методы анализа устойчивости будут рассмотрены в последующих главах). Если она устойчива, то показатели качества можно оценить по реакции системы на определенный входной сигнал. Но, поскольку обычно заранее неизвестно, каким в реальных условиях будет этот сигнал, при анализе качества выбирается некоторый тестовый входной сигнал. Такой подход вполне оправдан, т. к. имеется корреляция между реакцией системы на типовой входной сигнал и ее поведением в реальных рабочих условиях. Кроме того, использование типового входного сигнала позволяет проектировщику сравнить несколько вариантов создаваемой системы. К тому же многие системы управления в процессе эксплуатации подвергаются внешним воздействиям, которые по виду очень близки к тестовым сигналам.
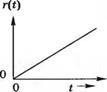
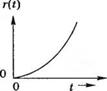
В качестве типовых тестовых сигналов обычно используются ступенчатый, линейный и параболический сигналы, изображенные на рис. 5.2. В табл. 5.1 приведены выражения для этих сигналов как функции времени, а также их преобразования по Лапласу, полученные с помощью табл. 2.3. Линейный сигнал является интегралом от ступенчатого, а параболический — интегралом от линейного.
|
Рис. 5.2. Тестовые входные сигналы: (а) ступенчатый, (б) линейный, [в) параболический |
|
|
|
|
|
в) |
|
О t — * а) б) |
|
r(t) А О |
|
Таблица 5.1. Тестовые входные сигналы
|
В качестве тестового сигнала может также служить единичная импульсная функ ция, получаемая из прямоугольного импульса
1/є, - е/2</<є/2;
/Е(0= n
О, при остальных t.
где є > 0. При 8 -> 0 импульс/Ё(0 стремится к единичной импульсной функции 8 (0, обладающей следующими свойствами:
Г S(t)dt = l, Г b(t-a)g(t)dt=g(a). (5.1)
J— 00 •'—СО
Импульсный входной сигнал может оказаться полезным, когда выходной сигнал jy(/) записывается в виде интеграла свертки
ЛО= - т)г(х)Л =i“' [С’0)Л0)]. (5.2)
J— СО
Эта связь изображена в виде структурной схемы на рис. 5.3. Если входной сигнал является единичной импульсной функцией, то
|
G(s) |
|
'Y(S) |
|
Щз)- |
|
(5.3) |
|
><0=f g(r-r)S(T)rfr. J— oo |
Рис. 5.3. Разомкнутая система управления
Этот интеграл отличен от нуля только при т = 0, поэтому
ЯО = g(0,
что соответствует импульсной переходной функции системы с передаточной функцией G(s). Реакция системы на импульсный тестовый сигнал может представлять интерес, если в реальных условиях система подвержена воздействию очень коротких импульсов с большой амплитудой и площадью А.
Типовые тестовые сигналы имеют общий вид
т = t' (5.4)
для которых преобразование Лапласа
|
R(s)=- |
|
и+1 |
|
Отсюда следует, что реакцию на один тестовый сигнал всегда можно выразить через реакцию на другой тестовый сигнал. Поскольку ступенчатый входной сигнал является наиболее простым, то его обычно и выбирают для оценки качества системы. Найдем реакцию системы, изображенной на рис. 5.3, на единичную ступеньку, если 9 G(s) = —. .s+10 Тогда преобразование по Лапласу для выходного сигнала 9 П*) = — , ф+10) переходный процесс описывается выражением y{t) = 0,9(1-£Г10'), а его установившееся значение, у(°о) = 0,9. Для установившейся ошибки, приняв £(s) = R(s) - 7(s), имеем е = lims£(.v) = 0,L л—>0 |