СОВРЕМЕННЫЕ СИСТЕМЫ УПРАВЛЕНИЯ

Структурные схемы

Динамические системы, в том числе и системы автоматического управления, на языке ма­тематики описываются системой обыкновенных дифференциальных уравнений. Как было отмечено в предыдущих разделах, использование преобразования Лапласа сводит задачу решения дифференциальных уравнений к решению системы линейных алгебраических уравнений. Поскольку в системах управления путем изменения одних переменных произ­водится целенаправленное воздействие на другие переменные, то необходимо установить связь между этими переменными. Данную связь обычно представляют в виде передаточ­ной функции, которая является одним из основных понятий теории управления.

Преимущество передаточной функции заключается в том, что она позволяет изобра­зить причинно-следственную связь между переменными в наглядной схематической фор­ме. В теории управления преобладает представление различных динамических систем в

Рис. 2.22

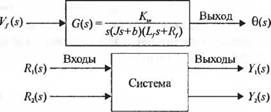
Структурная схема двигателя постоянного тока

Рис. 2.23

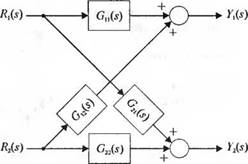
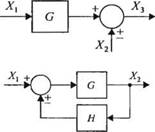
Система с двумя входами и двумя выходами

виде структурных схем. Структурные схемы состоят из блоков направленного действия, каждому из которых соответствует определенная передаточная функция. Так, на рис. 2.22 изображена структурная схема двигателя постоянного тока, управляемого по цепи воз­буждения, которая отражает связь между углом поворота 0(s) и приложенным напряже­нием Vf(s).

Для описания системы с несколькими управляемыми переменными используется структурная схема с перекрестными связями. Например, в системе на рис. 2.23 имеются две входных и две выходных переменных. С помощью передаточных функций мы можем записать связывающие их уравнения:

ВД = СИ(5)ВД + Gu(s)R2(s), (2.77)

У2(5) = G2l(s)Rx(s) + G22(s)R2(s), (2.78)

где G^s)—передаточная функция оту-го входа к У-му выходу. Структурная схема, отража­ющая записанные выше уравнения, представлена на рис. 2.24. В общем случае, при нали­чии./входов и/выходов, связывающие их уравнения можно записать в матричной форме:

или в компактном виде

Y = GR. (2.80)

Здесь У и R есть, соответственно, матрицы-столбцы, элементами которых являются 1 вы­ходных и J входных переменных, a G — матричная передаточная функция размерности JxJ.

4F Подобное матричное представление имеет особую ценность при анализе много - связных (многомерных) систем управления. Для читателей, не знакомых с алгеброй матриц, основные сведения из этой области приводятся на Web-сайте MCS.

Рис. 2.24

Структурная схема системы с перекрестными связями

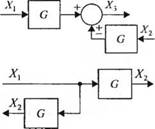
Пользуясь определенными правилами, структурную схему сложной системы можно упростить, сведя ее к конфигурации с меньшим числом блоков, чем в исходной системе. Поскольку передаточные функции являются средством описания линейных систем, им присуще свойство коммутативности. Следовательно, для поз. 1 из табл. 2.6 мы можем за­писать:

X3(s) = G2(s)X2(s) = С,(*)С2(4ад.

Если два блока соединены последовательно, то предыдущее уравнение можно запи­сать также в виде

ВД = G2(s)Gl(s)A'l(s).

При этом предполагают, что если выход первого блока соединен со входом второго, то влияние нагрузки на первый блок является незначительным. Если же нагрузка оказы­вает существенное влияние на выходную переменную предшествующего блока, то инже­нер обязан учесть этот фактор и внести соответствующее изменение в передаточную фун­кцию.

Таблица 2.6. Правила преобразования структурных схем

Исходная диаграмма Эквивалентная диаграмма

4. Перенос узла через блок с передаточной функцией по ходу движения сигнала

с

5. Перенос сумматора через блок с передаточной функцией против движения сигнала

6. Исключение контура с обратной связью

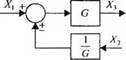
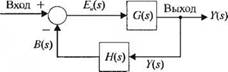
Методы преобразования структурных схем основаны на рассмотрении алгебраиче­ских соотношений между отдельными переменными. Например, рассмотрим структур­ную схему, изображенную на рис. 2.25. В этой системе с отрицательной обратной связью сигнал на входе объекта управления записывается в виде :

£„(.s) = R(s) - B(s) = R(s) - n(s)Y(s). (2.81)

Поскольку выходная переменная связана с этим сигналом передаточной функцией C(.v), то

Y(s) = G(s)Ea(s) (2.82)

и, следовательно,

ад = едем - /адвд]. (2.83)

Группируя члены при Y(s), получим:

y(s)[l + С(5)Я(5)] = G(s)R(s). (2.84)

Отсюда получим передаточную функцию, связывающую выход со входом: Y(s)_ G(s)

(2.85)

R(s) 1+G(s)N(s)

Это выражение, известное как передаточная функция замкнутой системы, представляет особую ценность, т. к. оно свойственно большинству реальных систем управления. Сведение структурной схемы, представленной на рис. 2.25, к одному-единственному блоку является лишь одним примером элементарных преобразований, приведенных в табл. 2.6. Анализ систем путем преобразования структурных схем дает гораздо лучшее представление о роли каждого элемента, чем это было бы при рассмотрении уравнений. Правила преобразования структурных схем мы проиллюстрируем на примере сведения многоконтурной системы к более простому виду.

Рис. 2.25

Система с отрицательной обратной связью

Пример 2.7. Упрощение структурной схемы

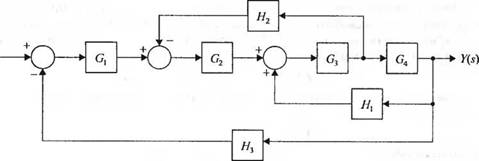
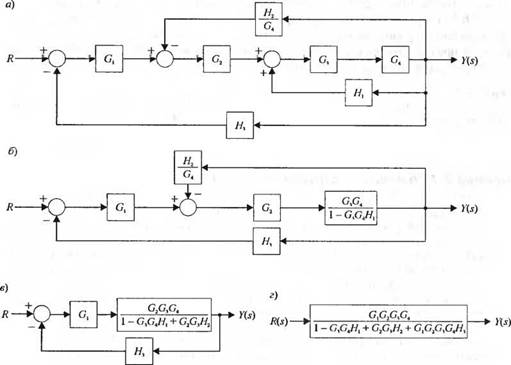
На рис. 2.26 изображена структурная схема многоконтурной системы управления. Заметим, что сигнал Hx(s)Y(s) подается на сумматор со знаком плюс, поэтому контур, образованный блоками G3(s)Gt(s)Ht(s), называют контуром с положительной обратной связью. Упрощение этой структурной схемы основано на применении правила 6 из табл. 2.6, которое связано с исключением изолированных контуров. Поэтому необходимо будет использовать и другие правила, чтобы подготовить схему к применению правила 6. Сначала, чтобы исключить кон­тур G3G4Hb мы перенесем узел через блок G4 по ходу движения сигнала (см. правило 4) и по­лучим схему, изображенную на рис. 2.21(a). Исключая контур G3G4//| по правилу 6, мы полу­чим схему рис. 2.21(6). Затем, исключая внутренний контур, содержащий Н2/С4, получим схе­му рис. 2.27(e). Наконец, исключая контур, содержащий Нъ, мы получим передаточную функ­цию замкнутой многоконтурной системы, как показано на рис. 2.21(г). Стоит обратить внимание на вид числителя и знаменателя этой передаточной функции. Можно видеть, что числитель образован произведением передаточных функций блоков, находящихся в прямой цепи от входа R(s) к выходу Y(s). Знаменатель равен единице минус сумма произведений пере­даточных функций блоков, образующих замкнутые контуры. Произведение G3G4Ht берется со

знаком плюс, поскольку это контур с положительной обратной связью, а произведения СОгСъС4Н3 и G2G3H2 — со знаком минус, т. к. в этих контурах обратная связь отрицательная. Чтобы лучше это проиллюстрировать, знаменатель можно записать в виде

= I — (+G3G4//] — GiGiHi — (і ] ОЧО'іОУ/з). (2.86)

Как мы увидим в следующем разделе, такой вид числителя и знаменателя характерен для мно­гоконтурных систем управления.

Метод структурных схем широко распространен в теории и практике автоматическо­го управления. Он дает очень наглядное графическое представление о взаимосвязи управ­ляемых и входных переменных. Кроме того, проектировщик легко может обнаружить не­обходимость введения в существующую структурную схему дополнительных блоков с целью улучшения характеристик системы. Наряду со структурными схемами существует альтернативный метод представления модели систем в виде сигнального графа. Этот ме­тод будет представлен в следующем разделе.