СОВРЕМЕННЫЕ СИСТЕМЫ УПРАВЛЕНИЯ
Модели в виде сигнальных графов
Структурные схемы адекватно представляют взаимосвязь между управляемыми и входными переменными. Однако для систем достаточно сложной конфигурации процедура упрощения их структурных схем является весьма трудоемкой и часто трудно выполнимой. Мейсоном был предложен альтернативный метод представления взаимосвязи между переменными системы, основанный на использовании сигнальных графов. Преимущество этого метода состоит в том, что по сигнальному графу, без каких-либо его преобразований, с помощью специальной формулы сразу можно установить связь между переменными системы.
Сигнальный граф представляет собой диаграмму, состоящую из узлов, соединенных между собой отдельными направленными ветвями, и является графическим средством описания линейных соотношений между переменными. Сигнальные графы особенно важны для систем управления с обратной связью, поскольку теория этих систем в первую очередь рассматривает распространение и преобразование сигналов. Основным элементом сигнального графа является однонаправленный отрезок, называемый ветвью, который отражает зависимость между входной и выходной переменной наподобие того, как это делает отдельный блок в структурной схеме. Например, ветвь, связывающая выход двигателя постоянного тока 0(s) с напряжением возбуждения Vf(s), изображенная на____ q ^ q 0(v)
рис. 2.28, подобна структурной схеме на
рис. 2.22. Точки входа и выхода, на рисун - Рис. 2.28. Сигнальный граф двигателя
ке похожие на клеммы, называются узла - постоянного тока
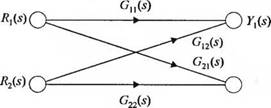
ми. Аналогично, сигнальный граф, соответствующий уравнениям (2.77), (2.78) и рис. 2.24, изображен на рис. 2.29. Преобразование каждой переменной охарактеризовано надписью около направленной стрелки. Все ветви, выходящие из узла, предают сигнал другому (выходному) узлу каждой ветви, причем однонаправленно. Сумма всех сигналов, входящих в узел, образует соответствующую этому узлу переменную. Путь — это ветвь или последовательность ветвей, которые могут быть проведены от одного узла к другому. Контур — это замкнутый путь, который начинается и заканчивается в одном и том же узле, причем вдоль этого пути ни один другой узел не встречается дважды. Некасающимися называются такие контуры, которые не имеют общего узла. Два касающихся контура имеют один или более общих узлов. Рассмотрев еще раз рис. 2.29, мы можем записать:
У,(5) = С„(5)ВД + Gl2(s)R2(s), (2.87)
y2(s) = G21(s)fl,(s) + G22(s)R2(s), (2.88)
|
|
|
ад |
|
Рис. 2.29. Сигнальный граф для системы с перекрестными связями |
|
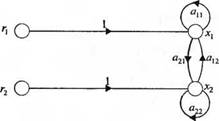
Рис. 2.30. Сигнальный граф для двух алгебраических уравнений |
Сигнальный граф — это просто наглядный метод записи системы алгебраических уравнений, показывающий взаимосвязь между переменными. В качестве еше одного примера рассмотрим следующую систему алгебраических уравнений:
|
(2.90) |
«11*1 + «12*2 + ri= х1> (2.89)
«21*1 + «22*2 + Г2= х2.
Здесь гхиг2 — входные переменные, axj их2 — выходные переменные. Сигнальный граф, соответствующий уравнениям (2.89) и (2.90), изображен на рис. 2.30. Уравнения (2.89) и (2.90) можно записать в ином виде:
|
(2.91) (2.92) (2.93) (2.94) |
*i(! - flu) + Х2І - ап) = ri,
*l( - a2l) + *20 - «22> = г2 ■
Решая последнюю систему по правилу Крамера, получим:
|
Яр г, +~^г2, А а~> г2 + —П- д |
X (~а2гУ+аПг2 _ (1-^22 )
1 (1 —«11 )(1 —«22 ) —«12«21 А
_ _ О-Oil >2 +«21'І (1-«ц)
Л-}-------------------------------------------------
(1 —аП )(1-«22 )_а12а21 Д
В этих решениях знаменатель равен определителю, составленному из коэффициентов при неизвестных, и его можно записать так:
А = (1 — Яц)(1 — Я22) — Яі2а21 = 1 «11 а22 + аиа22 ~ а2а2- (2-95)
В данном случае знаменатель равен единице минус коэффициенты передачи отдельных контуров аи, «22 и а12а21 плюс произведение коэффициентов передачи двух некасающихся контуров ах і и а22. Контуры а22 иа12а21 являются касающимися, так же, как и контуры ахха а2а12-
В решении для X) по отношению ко входу гх числитель равен единице, умноженной на (1 - а22), т. е. значению определителя некасающегося пути от гх к хх. В решении для х, по отношению ко входу г2 числитель просто равен аХ2, т. к. этот путь касается всех контуров. Числитель выражения ДЛЯ х2 симметричен соответствующему числителю ДЛЯ Х|.
В общем случае линейная зависимость Тп между независимой переменной х, (часто называемой входной переменной) и зависимой переменной х, определяется по формуле Мейсона:
X Рцк &ijk
где Рф коэффициент передачи к-ГО пути ОТ переменной X, К переменной Xj,
А — определитель графа,
А1/к -- дополнительный множитель ДЛЯ пути Рф
|
П= 771=1,4=1 |
а суммирование производится по всем возможным к путям от xt кхг Дополнительный множитель Aljk равен определителю всех касающихся контуров при удалении А-го пути. Определитель А находится как
(2.97)
где есть коэффициент передачи q-то контура. Таким образом, правило вычисления А через значения Z,, L2, J-ъ ■■■, LN таково:
Д = 1 - (сумма коэффициентов передачи всех отдельных контуров) +
+ (сумма произведений всех возможных комбинаций из 2 некасающихся контуров) - - (сумма произведений всех возможных комбинаций из 3 некасающихся контуров) + + ...
Формула Мейсона часто используется в несколько упрощенном виде для определения связи между выходной переменной K(s) и входной переменной R(s), т. е.
(2.98)
А
где T(s) = Y(s)/R(s). Коэффициент передачи пути Рк (или Р,/к) определяется как непрерывная последовательность ветвей, простирающихся в направлении, указанном стрелками, причем ни один узел не встречается в этой цепи более одного раза.
Простоту и удобство применения данного метода мы проиллюстрируем несколькими примерами. Хотя формула (2.96) на первый взгляд кажется трудно воспринимаемой, всё же следует помнить, что она представляет обычный процесс суммирования, а не сложных преобразований.
Пример 2.8. Передаточная функция системы с параллельными путями
На рис. 2.31 изображен сигнальный граф с двумя параллельными путями. Примером системы управления, граф которой имеет несколько путей, может служить шагающий робот с несколькими конечностями. От входа R(s) к выходу K(s) ведут следующие пути: путь 1 — Р| = GlG2GiG4 и путь 2 — Р2 = G5G6G7G8.
Граф содержит четыре контура:
L = ^2^2’ L2 = G3//3, = СЬНЬ, Z-4 = С7У/7.
|
И |
Рис. 2.31
Сигнальный граф с двумя параллельными путями
Контуры и Ь2 не касаются контуров и Л4. Следовательно.
Д = 1 — (Ц + L2 + Л^ + L4 Х+ (/-]/•; + + /^/4 + І2І4). (2.99)
Дополнительный множитель определителя для пути 1 вычисляется в результате удаления из Д контуров, касающихся пути 1. Поэтому
L, = L, = 0 и Д, = 1 - (L3 + Ц).
Аналогично, дополнительный множитель для пути 2 принимает вид
Д2 = 1 — {L + L-y).
Таким образом, передаточная функция системы
T(s) = = ^1 + ^2^2 _ Gfi-f}fi4(1 - L3 - L4) + GfibGJ3b ^
R(s) A l-Ll-L2-L3-L4+LlL3 + LiL4+L2LJ + L2L4'
Пример 2.9. Двигатель, управляемый по цепи якоря
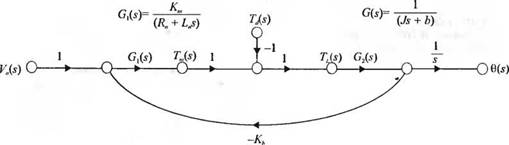
На рис. 2.20 изображена структурная схема двигателя постоянного тока, управляемого по цепи якоря. Схема отражает связь между переменными в виде уравнений (2.64)-(2.68). Сигнальный граф может быть получен либо на основании тех же уравнений, либо непосредственно по структурной схеме. Этот граф изображен на рис. 2.32. Полагая T/s) = 0, получим передаточную функцию 0(s)/ VJs) с помощью формулы Мейсона. Граф имеет прямой путь Р, (s), касающийся одного контура Lv(s), где
/j(s) = - G,(s)G2(j) и і,(ї) = - KhG^(s)G0(s).
s
Следовательно, передаточная функция имеет вид
Щ P'(S) ________ ёт________
l-A(s) І+КьС^уГф) $_{Ra + Las)Us+b)+KhKm что полностью совпадает с выражением (2.69). полученным ранее.
Формула Мейсона дает достаточно простой метод анализа сложных систем. Чтобы сравнить этот метод с методом упрощения структурных схем, который является ненамного более сложным, рассмотрим еще раз систему из примера 2.7.
Пример 2.10. Передаточная функция многоконтурной системы
На рис. 2.26 приведена структурная схема многоконтурной системы. Здесь нет особой необходимости перерисовывать эту схему в виде графа, поэтому мы сразу применим формулу Мейсона (2.98). Схема имеет один прямой путь l = GlG2G3G4 . Контуры в схеме таковы:
L = — G2G3H2, L2 — GiG4Hu Z-з = — G1G2G3G4W3. (2.101)
|
Рис. 2.32. Сигнальный граф двигателя постоянного тока, управляемого по цепи якоря |
Все контуры имеют общие узлы, поэтому они являются касающимися. Кроме того, путь Pt касается всех контуров, поэтому Л| = 1. Тогда передаточная функция замкнутой системы определяется выражением
У(і) _ /{Л, _
|
T(s) = |
(2.102)
R(s) 1 - Ц-L^-L^ 1 + С/;з//2 - С3С4//, + GfjjJfitH3
Пример 2.11. Передаточная функция сложной системы
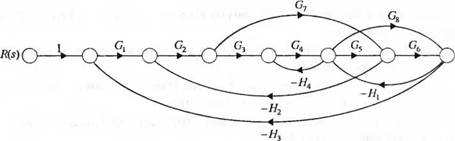
В заключение мы рассмотрим достаточно сложную систему, для которой метод упрощения структурной схемы представлял бы значительные трудности. Такая система с несколькими контурами и прямыми путями изображена на рис. 2.33. Прямые пути следующие:
/*| = GXG2G3G4G^G^, Р2 — Gj C^G-jG P3 — G|G2G3G4G^.
Кроме того, имеем следующие контуры:
L = — G2G3G4G$H2, L2 — — G$G(J/[, L3 = — GgHi, L4 = — С7//2С2, L3 = — GA/*.
L(, — — G (G2G3G4G sGbH3. L і — — GxG2GnG6H3, L% = — G yG2G3G4GgH3.
Контур Ls не касается контура Z,4 или контура Ly. контур L3 не касается контура 14; все остальные контуры являются касающимися. Поэтому определитель графа
Д = 1 — (Lі + Z.2 + L3 + L + L$ + Ьь + L^ + L$ ) + (L$Lq + L5L4 + L3L4). (2.103)
Дополнительные множители:
Ді — Д3 = 1 и Д2 = 1 - L5 = 1 + G4.W4.
Окончательно, передаточная функция имеет вид:
У(і) _ Р] + Р2А2+Р3
|
|
|
T(s)~ |
|
R(s) |
|
Рис. 2.33. Многоконтурная система |
(2.104)
r(s)