СОВРЕМЕННЫЕ СИСТЕМЫ УПРАВЛЕНИЯ
Пример синтеза: система управления лазерным манипулятором
В хирургии с помощью лазера можно высверлить углубление в берцовой кости для после-
дующего вживления искусственного сустава. Соответствующая установка должна иметь
достаточное быстродействие и высокую точность позиционирования. В системе, изобра-
женной на рис. 7.30, лазерный манипулятор управляется с помощью двигателя постоянно-
го тока. Коэффициент усиления К должен быть выбран так, чтобы при линейном входном
сигнале r(t) = At (где Л = 1 мм/с) установившаяся ошибка не превышала 0,1 мм и при этом
система оставалась устойчивой.
Рис. 7.30
Система
управления
лазерным
манипулятором
|
Чтобы обеспечить требуемую точность и высокое быстродействие, выберем электродвигатель с постоянной времени обмотки возбуждения Т[ = 0,1 с и с электромеханической постоянной времени (с учётом нагрузки) т2 = 0,2 с. Тогда мы получим: T{s)= KG(-S) = — =------------------------------------------ —- ---------- =— і®* .(7.119) +KG(s) s(i{s+l)(x2s+l)+K 0,02s3+0,3s2+s+K s3+ 15.Г + 50s+ 50A: Согласно (5.29), при линейном входном сигнале, R(s) =A/s2, установившееся ошибка равна А А 6ss~kv ~ К Поскольку при А = 1 мм/с должно выполнятся условие ess < 0,1 мм, то отсюда следует требование К > 10. Убедимся, что при К = 10 система будет устойчива. Для этого на основании (7.119) запишем характеристическое уравнение: j3 + 15s2 + 50s + 50 К = 0. Далее составим таблицу Рауса: 1 50 15 50Х Ьх 0 50К, |
|
Усилитель |
—► |
Двигатель и манипулятор |
|
К |
1 |
|
|
S(T, S+I)(V+1) |
|
-> ОД |
|
ад |
|
откуда следует Ьх = |
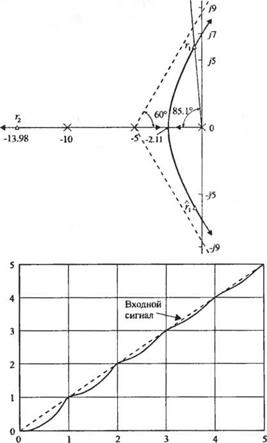
Таким образом, система устойчива при 0 < К < 15. Выбрав значение К= 10, при котором система устойчива, исследуем вид корневого годографа при К > 0. Поскольку годограф имеет три ветви, а центроид находится в точке а = - 5, то мы получим картину, изображённую на рис. 7.31. Точка отрыва имеет координату s = - 2,11, а при К = 10 равны г2 = - 13,98, г, = -0,51 + >5,96 и г,. Комплексным корням соответствует значение С, = 0,085 и <^со„ = 0.51. Считая эти корни доминирующими, мы можем ожидать, согласно (5.16) и (5.13), что при ступенчатом входном сигнале перереіулирование составит 76%, а время установления (по критерию 2% от конечного значения) будет равно
4 4
|
Т. = - |
= 7,8 с.
&»„ 0,51
|
|
|
уЧ) |
|
Не) |
Рассчитав и построив действительную реакцию системы на ступенчатый сигнал, мы обнаружим, что перерегулирование составляет 72%, а время установления равно 7,9 с. Таким образом, комплексные корни явно являются доминирующими. Очевидно, что система, обладающая сильно колебательной реакцией на ступенчатый сигнал, не может быть использована в лазерной хирургии, поэтому скорость изменения управляющего сигнала должна быть ограничена. Реакция той же системы на линейный входной сигнал приведена на рис. 7.32.
Рис. 7.31 Корневой годограф системы управления лазерным манипулятором
Рис. 7.32
Реакция системы управления лазерным манипулятором на линейный входной сигнал