СОВРЕМЕННЫЕ СИСТЕМЫ УПРАВЛЕНИЯ
Пример синтеза с продолжением: система чтения информации с диска
|
□ |
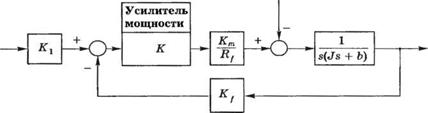
Синтез системы чтения информации с диска является примером оптимизации и принятия компромиссных решений. Система должна точно позиционировать считывающую головку и в то же время обладать способностью уменьшать влияние изменения параметров и внешних ударов и вибраций. Механический рычаг и пластина могут резонировать на частотах, с которыми появляются внешние возмущения, например тряска портативного компьютера. К числу возмущений относятся также физические удары, износ или биения в подшипниках привода, изменение параметров элементов системы. В этом разделе мы исследуем реакцию системы на возмущения и ее поведение при изменении параметров. Кроме того, получим оценку установившейся ошибки при ступенчатом изменении задания и пронаблюдаем, как повлияет на переходную характеристику изменение коэффициента усиления усилителя Ка. Таким образом мы выполним шаги 6 и 7 процедуры синтеза, представленной на рис. 1.19.
Возмущение
|
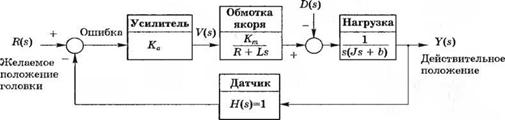
Рис. 4.32. Система управления положением считывающей головки дисковода |
Рассмотрим систему, изображенную на рис. 4.32. В этой системе в качестве регулятора используется усилитель с настраиваемым коэффициентом усиления. С учетом параметров, приведенных в табл. 2.11, мы получим структурную схему, изображенную на рис. 4.33. Сначала определим установившуюся ошибку при единичном ступенчатом входном воздействии, R(s) = І/s, полагая D(s) = 0. Поскольку H(s) = 1, то
£(*)=
l + KeGj(j)G2(j)
Следовательно,
|
lim e(t)= lim л’ t ->oo s—>0 |
|
(4.71) |
l
_і+ад(*)С72(*).
|
Отсюда следует, что е(°о) = 0 несмотря на любые изменения параметров системы. Возмущение
|
Теперь получим переходную характеристику системы при разных значениях коэффициента Ка. Передаточная функция замкнутой системы с учетом условия D(s) = 0 имеет вид:
Г(5) KaGl(sy02(s) _ 5000Ка
|
(4.72) |
T(s) =
R(s) l + KaG{ (s)G2 (s) s3 + 1020s2 + 20000s + 5000KL
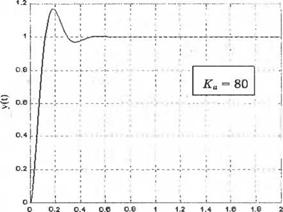
С помощью скрипта MATLAB, приведенного на рис. 4.34(a), мы получим переходные характеристики системы при значениях Ка = 10 и Ка = 80. Эти характеристики изображены нарис. 4.34(б). Очевидно, что система быстрее отрабатывает задающее воздействие в случае Ка = 80, но реакция имеет колебательный характер, что, по-видимому, неприемлемо.
|
Рис. 4.34 Переходные характеристики замкнутой системы. (а) Скрипт MATLAB. (б) Переходные характеристики при Ка =■ 10 и Ка = 80 |
|
я) |
|
Выбор Ka |
|
Ка=10; <------------------------------------ nf=[5000]; df=[1 1000]; sysf=tf(nf, df); ng=[1];dg=[1 20 0]; sysg=tf(ng, dg); sysa=series(Ka*sysf, sysg); sys=feedback(sy sa, [1 ]); t=[0:0.01:2]; step(sys. t); уІаЬеІ(‘у(і)’),хІаЬеІ(‘Время (c)‘),grid |
|
I : |
___ j |
||
|
....... ___________ j... |
1 . _. J |
||
|
... т~‘"Т -■-[.... |
........ I.... |
• 1 |
|
|
• ■- |
|||
|
її Ь-1 О |
1 . j |
||
|
/ |
-- |
і і |
|
|
7 - |
„„ |
1 , |
1 • і 1 |
|
О. Є 08 0.7 0.6 0.3 0.4 0.3 0.2 |
|
О 0.2 0-4 0.6 0.8 1 1.2 1.4 1.Є Время (с) |
|
Время (с) |
6)
Теперь определим влияние возмущения D(s) = І/s, полагая R(s) = 0. Желательно, чтобы это влияние было незначительным. На основании рис. 4.33 имеем:
у (5) =------------------------- £>(*)■ (4.73)
1 + ВД(лХ72(*)
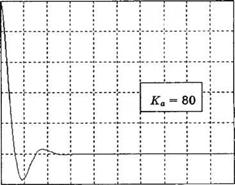
С помощью скрипта MATLAB, приведенного на рис. 4.35(a), при Ка = 80 и D(s) = 1/s мы получим реакцию системы, изображенную на рис. 4.35(б). Чтобы еще сильнее уменьшить влияние возмущения, нам потребовалось бы взять коэффициент Ка больше, чем 80. Однако при этом реакция системы на сигнал r(t) = 1, t > 0 была бы сильно колебательной. В следующей главе мы попытаемся определить оптимальное значение Ка, предъявив определенные требования к быстродействию системы и величине перерегулирования.
|
-і |
|
Рис. 4.35 Реакция на ступенчатое возмущение. (а) Скрипт MATLAB. (б) Реакция на возмущение при Ка = 80 |
|
|
|
6) о -0.5 |
|
S -1.5 |
|
О 0.2 0 4 О.0 С.8 1 1.2 1.4 16 1.8 2 Время (с) |
|
х Ю |
|
■2 3 |
Резюме
Основные мотивы использования обратной связи, несмотря на сопутствующие этому издержки и увеличение сложности системы, сводятся к следующему:
1. Уменьшение чувствительности системы к изменению параметров объекта управления.
2. Возможность воздействовать на вид переходной характеристики.
3. Ослабление влияния внешних возмущений и шумов, возникающих внутри системы.
4. Уменьшение установившейся ошибки системы.
|
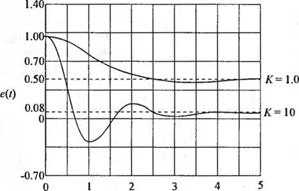
(а) Одноконтурная система управления. (б) Изменение ошибки при единичном ступенчатом возмущении в случае f/[s) = О |
|
-±о г |
|
ns) |
|
Время |
|
Преимущества введения обратной связи можно проиллюстрировать на примере системы, изображенной на рис. 4.36(a). При этом коэффициенту усиления К можно придавать разные значения. В табл. 4.4 приведены результаты исследования разомкнутой системы при К = 1 и замкнутой системы при трех различных значениях К. Из таблицы видно, что увеличение коэффициента усиления в замкнутой системе приводит к уменьшению времени нарастания переходной характеристики, чувствительности системы к изменению параметров и установившейся ошибки. На рис. 4.36(6) изображена реакция системы на единичное ступенчатое возмущение [при R(s) = 0], причем отчетливо видно, что увеличение коэффициента усиления также ослабляет влияние возмущения. Рис. 4.36 |
|
к |
-ла!_ |
і |
|
(*+i)2 |
|
D( S) |
|
о) |
|
б) |
|
Таблица 4.4. Характеристики системы, изображенной на рис. 4.36(e)
* Разомкнутую систему имеет смысл рассматривать только при К= 1. Системы управления с обратной связью обладают многими полезными свойствами, и неудивительно, что большое число таких систем можно встретить в промышленности, природе и общественной жизни. |
Упражнения
У-4.1. В устройствах электропитания от солнечных батарей используются системы с обратной связью, которые следят за положением Солнца с целью получения максимума отдачи мощности от батарей. Такая следящая системаможет быть представлена в виде рис. 4.3, где H(s) = 1 и
п л 100 G(s) =
TS + 1
причем номинальное значение т = 3 с. (а) Определите чувствительность системы к малым изменениям т. (б) Определите постоянную времени замкнутой системы.
Ответы: S = —3s/(3s+ 101); тс = 3/101 с.
|
D(s) |
Рис. 4.2 (У) Шум
Цифровая аудиосистема
Усилитель
|
V,(S) |
|
G(s) |
|
К. |
|
<> |
|
|
|
|
У-4.2. Цифровая аудиосистема проектируется так, чтобы минимизировать влияние возмущений и шума, как показано на рис. 4.2(У). В качестве аппроксимации можно принять G(s) = К2.
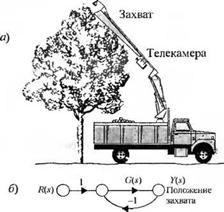
(а) Вычислите чувствительность системы к изменению Кг. (б) Оцените влияние возмущения на V0. (в) Какое значение К, вы бы выбрали, чтобы минимизировать влияние возмущения? У-4.3. На рис. 4.3(У), (а) показано, как можно использовать для сбора фруктов руку робота и телекамеру. Телекамера играет роль канала обратной связи, по которому сигнал поступает в микрокомпьютер, управляющий рукой.
Объект имеет передаточную функцию
G(g)= К.
(s+ З)2
(а) Определите установившуюся ошибку захвата при ступенчатом изменении задания величиной А как функцию параметра К.
(б) Укажите, что для данной системы может играть роль возмущающего воздействия.
д
Ответ', (а) е,,гт =---------- .
уст І+КІ9
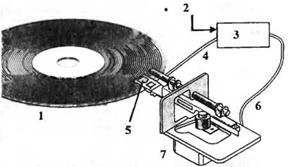
У-4.4. В дисководе компьютера позиционирова - Рис. 4.3 (У). Робот — сборщик фруктов ние головки записи/считывания над дорожками вращающегося магнитного диска осуществляется с помощью электродвигателя, как показано нарис. 4.4(У). Двигатель и головкамогут быть представлены передаточной функцией
G{s) = ——, s(xs + 1)
где т = 0,001 с. Контроллер определяет разность между желаемым и действительным положением головки и вырабатывает сигнал ошибки, который затем усиливается усилителем с коэффициентом К. (а) Чему равна установившаяся ошибка при ступенчатом изменении желаемого положения? (б) Определите требуемое значение К, при котором установившаяся ошибка составит 0,1 мм, если входной сигнал изменяется линейно со скоростью 10 см/с.
|
Ответ: е, |
= 0; К= 100.
уст
|
|
|
Рис. 4.4 (У) Система позиционирования головки записи/считывания дисковода. 1 — Магнитный диск, 2 — Желаемое положение, 3 — Контроллер, 4 — Сигнал датчика, 5 — Головка записи/считывания 6 — Вход двигателя, 7 — Двигатель |
|
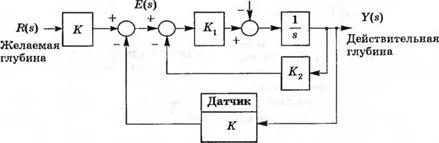
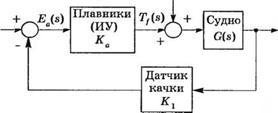
У-4.5. Большинству людей знакома ситуация нечеткой фокусировки диапроектора. Проектор с автоматической фокусировкой настраивается к изменению положения слайда и температурным возмущениям. Изобразите структурную схему системы автофокусировки и опишите принцип действия этой системы. Примером установившейся ошибки может служить визуальное наблюдение несфокусированного изображения слайда. У-4.6. В странах, где зимой дороги скользкие из-за снега и льда, большой популярностью пользуются полноприводные автомобили. В таких автомобилях в приводе на каждое из четырех колес используется датчик, позволяющий поддерживать постоянную силу сцепления. Структурная схема подобной системы изображена на рис. 4.6(У). Определите переходную характеристику этой системы, если она должна поддерживать постоянную скорость вращения колеса. С помощью компьютерной программы получите реакцию системы, если R(s) = A! s. У-4.7. Аппараты для подводного плавания с корпусом из прозрачного пластика могут произвести настоящую революцию в сфере досуга и развлечений. Один из таких небольших аппаратов имеет систему регулирования глубины, изображенную на рис. 4.7(У). (а) Определите передаточную функцию замкнутой системы T{s) = Y(s)/R(s). (б) Определите чувствительности системы Si, и SrK. (в) Определите установившуюся ошибку, вызванную возмущением D(s) = 1/s. |
|
5(s+2) s(s+10) |
|
R(s) |
|
. V(s) Скорость вращения колеса |
|
о— |
|
Рис. 4.6 (У). Система управления скоростью вращения колеса полноприводного автомобиля |
|
|
|
Возмущение |
|
D(s) |
Рис. 4.8 (У)
Замкнутая +
система R(s) —КО'
управления J
|
Регулятор |
||||
|
K(s + 50) |
41.67 |
|||
|
(s + 200) |
(s2+ 16.7s + 83.3) |
|
Датчик |
||
|
500 |
||
|
(s + 500) |
(г) Вычислите реакцию y(t) на воздействие R(s) = І/s, если К = К2 = 1 и 1 < К, < 10. Выберите значение соответствующее максимальному быстродействию системы.
У-4.8. Рассмотрите замкнутую систему управления, изображенную на рис. 4.8(У). (а) Определите установившуюся ошибку при ступенчатом входном воздействии как функцию коэффициента усиления К. (б) Определите максимальное перерегулирование на переходной характеристике при 40 < К < 400. (в) Постройте графики зависимости перерегулирования и установившейся ошибки от параметра К.
Задачи
3-4.1. Передаточная функция проточного бака, полученная в задаче 2.12, может быть записана в виде
Ag200 . ____
Ag,(s) ті - + l’
|
C(s) = |
1
где т = RC. Здесь R ■— ко) істанта, эквивалентная гидравлическому сопротивлению выходного отверстия, так что 1/R = (/2)кНц Ьг, а С — площадь поперечного сечения бака. Так как Н = RAQ2. то передаточная функция, связывающая изменение уровня жидкости с приращением входного потока, имеет вид:
|
R |
|
Г ЗЖЕ |
|
АС^ |
|
+ |
|
Q |
|
&Q |
|
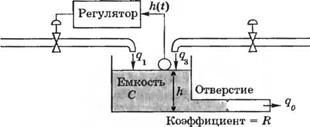
Н Рис. 4.1 (3). Регулирование уровня в проточном баке |
|
Ag|0) RCs + 1 Для образования замкнутой системы регулирования уровня можно использовать поплавковый датчик и вентиль, как показано на рис. 4.1(3). Пренебрегая массой поплавка, можно считать, что вентиль уменьшает величину входного потока пропорционально увеличению уровня, т. е. Л(2| = КАН. Изобразите сигнальный граф или структурную схему замкнутой системы. Определите и сравните следующие показатели разомкнутой и замкнутой систем: (а) чувствительность к изменению эквивалентного па- |
|
G,(s) = |
|
ДH(s) |
раметра R и коэффициента обратной связи К: (б) способность к уменьшению влияния возмущений по уровню ДH(s); (в) установившуюся ошибку по уровню при ступенчатом изменении входного потока Д{2|(я)-
3-4.2. На морских судах очень важно создать пассажирам комфортные условия за счет ослабления качки, обусловленной волнами. Большинство систем стабилизации используют для этого специ-
|
|
|
Влияние волн ад |
|
Угол качки 0(s) |
|
Рис. 4.2 (3). Система стабилизации судна. Влияние волн характеризуется моментом Т(] (s), приложенным к судну |
|
, Плавник |
|
Плавник |
|
|
|
о) |
|
б) |
альные плавники или подводные крылья, посредством которых судну сообщается стабилизирующий момент. Принцип действия такой системы стабилизации поясняется рис. 4.2(3). Бортовую качку судна можно рассматривать как колебания маятника с отклонением от вертикали в 0 градусов и периодом 3 с. Качке судна в этом случае соответствует передаточная функция
С(*) = -5------ ^-------- 2 ’
s + + ы„
где сов = 3 рад/с и С, = 0.20. При таком малом значении коэффициента затухания Q колебания продолжаются в течение нескольких периодов, а их амплитуда может достигать 18° при обычных морских волнах. Определите и сравните следующие показатели для разомкнутой и замкнутой систем: (а) чувствительность к изменению коэффициентов исполнительного устройства Ка и датчика качки Kt; (б) способность уменьшать влияние ступенчатых возмущений со стороны волн. Учтите, что желаемое значение угла 0 равно нулю.
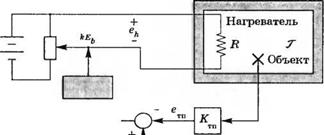
3-4.3. В промышленности и химической технологии одной из наиболее важных переменных, подлежащих управлению, является температура. Простой пример системы регулирования температуры приведен на рис. 4.3(3). Температура Т внутри объекта создается нагревателем с сопротивлением R. В линейном приближении теплоотдача от объекта в окружающую среду пропорциональна разности температур (Т— Тс). Последнее справедливо в случае, когда разность температур относительно невелика и когда накоплением энергии нагревателем и стенками объекта можно пренебречь. Предполагается также, что напряжение, подводимое к нагревателю, е1г пропорционально желаемому значению еф т. е. eh = kEh = klrEbe(t), где Ка — коэффици-
|
|
|
Исполнительное 11 e(t) устройство |
|
Окружающая среда |
|
Термопара |
ент передачи исполнительного устройства. Тогда для линеаризованной системы без обратной связи можно записать уравнение:
Г(*) = -
XS + 1
где
т = МС/рА, М — масса внутри объекта, А — площадь поверхности объекта,
р — коэффициент теплопередачи. С — удельная теплоемкость,
к{ — размерный коэффициент, етп — выходное напряжение термопары.
Определите и сравните следующие показатели разомкнутой и замкнутой систем: (а) чувствительность к изменению коэффициента К = k{kcfib; (б) способность уменьшать влияние ступенчатого изменения температуры окружающей среды ATe(s) (в) установившуюся ошибку регулятора температуры при ступенчатом изменении входного сигнала ed.
|
|
|
R(s) Вход |
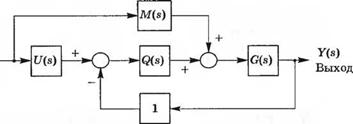
3-4.4. Система управления имеет два прямых пути передачи сигнала, как показано на рис. 4.4(3).
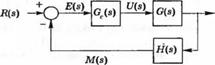
(а) Определите передаточную функцию T(s) = Y(s)/R(s). (б) Используя выражение (4.16). определите чувствительность (в) Зависит ли чувствительность от U(s) или от M(s)r>
Рис. 4.4 (3)
Система с двумя прямыми путями
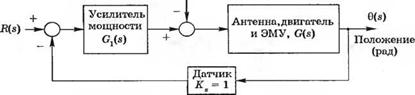
3-4.5. В радиоастрономии и системах слежения за спутниками используются большие антенны, работающие в микроволновом диапазоне. На такую антенну, имеющую диаметр 18 м, действует возмущающий момент, создаваемый сильными порывами ветра. Предположим, что ошибка в положении антенны не должна превышать 0,1 ° при скорости ветра 60 км/ч. Экспериментально установлено, что ветер такой силы создает возмущающий момент 27600 кгм, что эквивалентно напряжению на входе электромашинного усилителя, равному 10 В. Следящая система управления антенной изображена на рис. 4.5(3), где возмущение представлено сигналом TJs). Передаточная функция антенны, приводного двигателя и электромашинного усилителя имеет вид:
w Vа/ — 9 9 9
s(s + 2Q<4tls + ш„)
где шв = 15 и Q = 0,707. Усилитель мощности имеет передаточную функцию G,(s) = KJ(ts+l). где т = 0,15 с. (а) Определите чувствительность системы к изменению параметра Ка. (б) На систему действует возмущение TJs) = 10/s. Полагая R(s) = 0, определите требуемое значение коэффициента Ка, при котором установившаяся ошибка не будет превышать 0,1°. (в) При том же возмущении TJs) = 10/s и R(s) = 0 определите ошибку системы, если она является разомкнутой (К, = 0).
|
|
|
|
|
Момент нагрузки AD(s) |
|
V(s) Скорость |
|
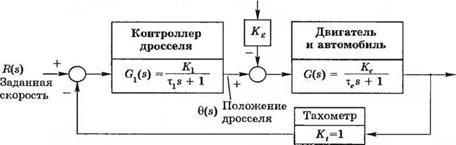
Рис. 4.6 (3). Система управления скоростью автомобиля |
3-4.6. Легковые автомобили, движущиеся по автоматизированным автострадам будущего, должны будут оснащаться системами автоматического управления скоростью. Модель такой системы с обратной связью изображена на рис. 4.6(3), где также показано возмущение AD(s) в виде момента нагрузки из-за подъема дороги. В различных моделях автомобилей коэффициент передачи двигателя Ке варьируется в диапазоне от 10 до 1000. Постоянная времени двигателя хе = 20 с. (а) Определите чувствительность системы к изменению параметра Ке. (б) Определите влияние момента нагрузки на скорость, (в) Определите величину постоянного угла подъема AD(s) = Дd/s, при котором автомобиль остановится, т. е. скорость F(s) станет равна нулю, и выразите эту величину в зависимости от коэффициентов передачи элементов системы. Учтите, что поскольку угол подъема — постоянный, то достаточно исследовать установившийся процесс. Предположите, что R(s) = 30/s км/ч и что КеКх з> 1. Если KJK, = 2, то при каком угле подъема Ad автомобиль остановится?
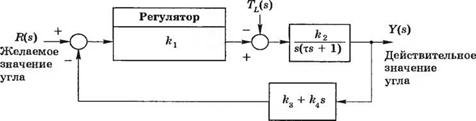
3-4.7. В роботах обратная связь используется для управления углом поворота в каждом сочленении. Изменение нагрузки, обусловленное переносимыми объектами, в конечном счете приводит к изменению положения руки робота. Таким образом, рука робота будет отклоняться от желаемой траектории за счет нагрузки, переносимой захватом. Система управления может быть представлена в виде рис. 4.7(3), где момент нагрузки TL(s) = D/s. Предположим, что в исходном состоянии R(s) = 0. (а) Определите влияние TL(s) на >’(s). (б) Определите чувствительность замкнутой системы к изменению параметра к2. (в) Чему будет равна установившаяся ошибка, если R(s) = І/s и TL(s) = 0?
3-4.8. Большие перепады температур часто приводят к отказу электронных схем. Для уменьшения влияния низкой температуры окружающей среды используется система с обратной связью, включающая в себя нагревательный элемент. Структурная схема такой системы изображена на рис. 4.8(3). Влияние понижения температуры окружающей среды отражено ступенчатым
|
Возмущение (нагрузка)
|
|
Рис. 4.8 (3) Система регулирования температуры |
|
Электронная схема |
|
R(s) |
|
Y(s) |
|
ОД |
|
Нагреватель |
+ |
|
|
К |
||
|
0.2s + 1 |
+ ( |
|
D(s) |
возмущением D(s). Действительному значению температуры электронной схемы еиогветству - ет У(і). Динамика изменения температуры схемы характеризуется передаточной функцией
ЮО
G(s) = —--------------- .
s2 + 20s + 100
(а) Определите чувствительность системы к изменению параметра К. (б) Оцените влияние возмущения £>(s) на выходную переменную y(s).
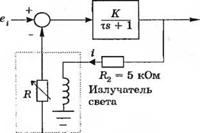
3-4.9. В качестве чувствительных элементов часто применяются датчики, в состав которых входит излучатель света (светодиод). Световой поток излучателя, который зависит от протекающего через него тока, изменяет сопротивление фоторезистора. Светодиод и фоторезистор находятся в одном корпусе с четырьмя выводами. Такой прибор обладает большим коэффициентом усиления и обеспечивает полную электрическую развязку. На рис. 4.9(3), (я) изображена схема с обратной связью, использующая этот прибор, а на рис. 4.9(3), (б) приведена нелинейная зависимость сопротивления от тока для прибора Рейтон СК1116. Эта зависимость может быть описана выражением
0,175
|
,1/2 ' |
lg* =
(і - 0,005)'
где і—ток, протекающий через излучатель. Рабочей точке соответствуют значения е0 = 35 В и е; = 2,0 В. (а) Определите передаточную функцию замкнутой системы, (б) Определите чувствительность системы к изменению параметра К.
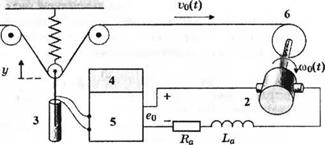
3-4.10. В бумажном производстве очень важно поддерживать постоянное натяжение полосы бумаги между двумя рулонами, с одного из которых бумага сматывается, а на другой наматывается. Это натяжение меняется в зависимости от толщины рулонов, поэтому необходимо управлять скоростью вращения двигателя на приемной стороне, как показано на рис. 4.10(3). Если скорость двигателя не регулировать, то по мере перемотки бумаги скорость v0 падает, что приводит к уменьшению натяжения. Для измерения натяжения бумаги используется комбинация из трех роликов и пружины. Упругая сила равна к$>, а линейный дифференциальный трансформатор, выпрями-
|
S О |
|
ЮМ 1М 100k 10k lk 100 |
|
1 |
|||||||||
|
1 |
|||||||||
|
ч |
|||||||||
|
0123456789 10 Ток через излучатель (мА) |
|
б) |
|
(J) Источник I постоянного — тока |
|
о, о н о. о t- о «• ф к и о К и к ь* о & G О О |
|
а) |
|
|
|
Рис. 4.10 (3). Система управления натяжением бумаги 1 — Разматываемый рулон, 2 — Двигатель, 3 — Линейный дифференциальный трансформатор, 4 — Выпрямитель, 5 — Усилитель, 6 — Наматываемый рулон |
|
vi (t) |
|
|
тель и усилитель можно описать уравнением е0 = - к^у. Таким образом, степень натяжения описывается соотношением 2T(s) = ку, где у— отклонение от равновесного состояния, a T(s) - вертикальная составляющая отклонения натяжения от эталонного значения. Двигатель имеет постоянную времени т = LJR„, а линейная скорость приемного рулона в два раза больше угловой скорости двигателя, т. е. v0(t) = 2ы0(/). Тогда двигатель можно описать уравнением
Е0 (і) = [tsco0 (s) + со0 (і)] + к, АГ (4
т
где АТ — возмущение по натяжению бумаги, (а) Изобразите структурную схему замкнутой системы с учетом возмущения AT(s). (б) В полученной структурной схеме учтите дополнительно возмущение со стороны скорости разматываемого рулона ДК,(«). (в) Определите чувствительность системы к изменению постоянной электродвигателя Кт. (г) Определите установившуюся ошибку по натяжению, вызванную ступенчатым изменением скорости AV{s) = Als.
3-4.11. При производстве бумаги очень важно поддерживать постоянную плотность исходной массы перед тем, как она поступает на сушку и протяжку. На рис. 4.11(3), (а) приведена схема управления плотностью бумажной массы. Плотность определяется количеством добавляемой в смеситель воды. Структурная схема данной системы изображена на рис. 4.11 (3), (б). Предположим, что H(s) = 1 и
ад=-^-, c(s)=- 1
|
8s + 1 |
4s + 1
|
о) |
Вода
|
_l |
-R(s) - заданное значение плотности
|
U(s) |
|
M(s) |
|
X |
|
Регулятор |
|
Вентиль |
|
Измерение плотности |
|
ж Перемешивание пульпы |
|
Производство бумаги |
|
|
Определите (а) передаточную функцию замкнутой системы T(s) = Y(s)/R(s), (б) чувствительность SJK и (в) установившуюся ошибку при ступенчатом изменении заданного значения плотности R(s) = A/s. (г) Вычислите значение К, при котором установившаяся ошибка будет составлять 1% от заданного значения плотности.
|
|
|
Рис. 4.12 (3). Две системы с обратной связью |
|
а) |
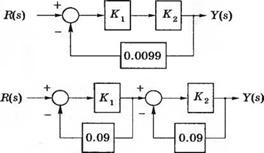
3-4.12. На рис. 4.12(3) изображены
|
б) |
структурные схемы двух систем с обратной связью, (а) Определите передаточные функции T,(s) и T2(s) для этих систем в замкнутом состоянии, (б) Покажите, что при КХ=К2 = 100 Г, = Тг = 100. (в) Сравните чувствительности двух систем по отношению к параметру К, при номинальных значениях Кх = К2 = 100.
3-4.13. Передаточная функция некоторой замкнутой системы представлена в виде
|
Г(а) = |
G,(s) + kG2(s)
G3(s) + kGi(s)
(а) Используя выражение (4.16), покажите, что
|
Si =- |
k(G2C, - G, G4)
(G3 + kGA ) (G, + kG2)
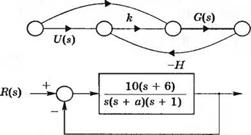
(б) С помощью того же выражения определите чувствительность системы, граф которой изображен на рис. 4.13(3).

|
M(s) |
|
R(s) |
|
Y(s) |
|
|
Рис. 4.13 (3)
Система с обратной связью
|
Yi[s) Скорость полета |
Рис. 4.14 (3)
Система управления скоростью сверхзвукового самолета
3-4.14. Проектируемый сверхзвуковой самолет должен лететь со скоростью 6000 км /ч на высоте 30 км и пересекать. Тихий океан за 2 часа. Система управления скоростью такого самолета может быть представлена в виде модели, изображенной на рис. 4.14(3). Определите чувствительность передаточной функции замкнутой системы T(s) к малым изменениям параметра а.
3-4.15. На рис. 4.15(3) изображена структурная схема системы управления курсом движения современного морского судна. При К = 5кК = 25 определите в установившемся режиме эффект, создаваемый ветром постоянной силы, т. е. возмущением D(s) = І/s. (а) Решите задачу в предположении, что положение руля R(s) = 0, т. е. оно не изменяется, (б) После этого покажите, что за счет изменения положения руля отклонение судна от заданного курса можно свести к нулю.
3-4.16. На рис. 4.16(3) изображена модель системы, состоящей из двух баков, где Т0 есть температура жидкости, втекающей в первый бак, а Т2 — температура жидкости, вытекаюшей из второго бака Последний снабжен нагревателем, тепловой мощностью которого, Q, можно управлять. Значения постоянных времени т, = 10 с и т2 = 50 с. (а) Получите выражение для T2(s) в зависи-
 Возмущение, создаваемое ветром
Возмущение, создаваемое ветром
D(s)
|
& |
|
100 |
|
Y(s) |
|
R(s) — Положение руля |
|
К |
|
s + 10s + 100 |
|
Отклонение судна от заданного курса |
|
|
|
Рис. 4.15 (3). Система управления курсом движения судна |
|
Рис. 4.16 (3) Регулирование температуры в системе из двух баков |
мости от T0(s) и T2c{s). (б) В случае, когда заданное значение температуры T2(^s) меняется скачком от T2lfs) = A/s до TtJs) ~ 2A/s, причем Tn(s) = Als, определите переходную характеристику T2(t) при Gc(s) = К = 500. (в) Для условий из п. (б) определите установившуюся ошибку еи, считая, что E(s) = T2lf s) - T2(s).
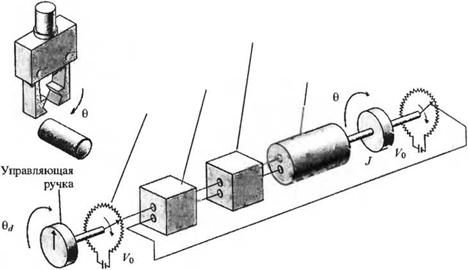
3-4.17. Захват робота, изображенный нарис. 4.17(3), (а), должен управляться таким образом, чтобы он замыкался на заданный угол 0. Это осуществляется с помощью системы, включающей двигатель постоянного тока, которая схематически изображена на рис. 4.17(3), (б). Модель данной системы управления представлена на рис. 4.17(3), (в), где Кт = 30, R,= 1 Ом, К/= К, = 1. J = 0,1 иі=1. (а) Определите реакцию системы, 0(0, на ступенчатое изменение 0,/f) при К = 20.
(б) Полагая 0t/(f) = 0, оцените эффект, создаваемый возмущением по нагрузке TJs) = A/s.
(в) Определите установившуюся ошибку еи. при входном сигнале r(t) = /, t > 0. (Предположите, что Та = 0.)
Усилитель
|
Усилитель рассогласования |
мощности
|
Потенциометр |
Двигатель
Сигнал обратной связи
б)
TJL s)
|
Рис. 4.17 (3). (продолжение) |
|
в(в) |
е)
в»
Задачи повышенной сложности
ГІ-4.1. Нарис. 4.1(П), (а) изображена система регулирования уровня жидкости в баке. Задача состоит в поддержании постоянного уровня h вне зависимости от возмущения qv На том же рисунке ниже приведена структурная схема системы для малых отклонений переменных от состояния равновесия, так что заданное значение htf t) = 0. Получите выражение для ошибки в виде E(s) и найдите ее установившееся значение в случае единичного ступенчатого возмущения, если (а) G(s) = К и (б) G(s) = K/s.
П-4.2. Для управления движением плеча руки робота используется двигатель постоянного тока, управляемый по цепи якоря, причем вал двигателя соединен с редуктором. На рис. 4.2(П) изображена структурная схема системы управления, на которой указано возмущение в виде момента нагрузки D(s) Определите установившуюся ошибку, если заданное значение угла поворота 6js) = A/s, Gc(s) = А' и возмущение отсутствует. Определите также установившуюся ошибку, если 0» = 0. а возмущение D(s) = M/s, в случаях (a) Gc(s) = К и (б) Gc(s) = K/s. П-4.3. Рабочий орган станка должен перемещаться по траектории, задаваемой уравнением
r(t) = (2 - f + 0,5г)и(/),
где u(t) — единичная ступенчатая функция. На рис. 4.3(П) изображена структурная схема системы управления перемещением рабочего органа.
(а) Определите установившуюся ошибку при заданном сигнале r(t) в случае, когда D(s) = 0.
(б) На основании п. (а) изобразите график e(t) для 0 < г < 10 с.
|
|
|
уровня Рис. 4.1 (П). Регулятор уровня жидкости в баке |
|
Возмущение (нагрузка)
Рис. 4.2 (П). Система управления звеном руки робота |
Влияние
|
Двигатель и рабочий орган |
|
Y(s) |
|
ад |
|
s(s + 3) |
|
Управляющий сигнал |
|
Положение рабочего органа |
|
Регулятор |
||
|
*- |
5(s + 1) |
|
|
S |
|
гО |
|
нагрузки D(s) |
Рис. 4.3 (П). Система управления положением рабочего органа
(в) В случае r(t) = 0 определите установившуюся ошибку при D(s) = 1/s.
(г) На основании п. (в) изобразите график e(t) для 0 <1< 10 с.
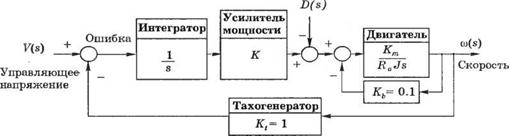
П-4.4. На рис 4.4(П) приведена структурная схема двигателя постоянного тока с управлением по цепи якоря и тахометрической обратной связью. Параметры системы: Кт — 10, J = 1 и Ra — 1.
(а) Определите значение К, при котором установившаяся ошибка при отработке линейного входного воздействия v(/) = /, / > 0 не будет превышать значения 0,1 (в предположении, что D(s) = 0).
(б) При коэффициенте К, найденном в п. (а), получите выражение и изобразите график для ошибки e(t) при действии линейного возмущения d(t) = 1, 0 < / < 5 с.
П-4.5. В настоящее время создана и прошла испытания система, регулирующая среднее артериальное давление во время анестезии. Было показано, что уровень артериального давления является показателем глубины анестезии во время хирургической операции. На рис. 4.5(П) изображена структурная схема такой системы, где хирургическое вмешательство учтено в виде возмущения D(s).
(а) Полагая R(s) = 0, определите установившуюся ошибку, вызванную возмущением D(s)~l/s.
|
Рис. 4.4 (П). Двигатель постоянного тока с тахометрической обратной связью |
|
Хирургическое ■D(s) Газовая |
|
Пациент |
Y(s) |
|
1 |
|
|
(S + 2)2 |
Действительное |
|
|
|
О* |
|
Желаемое давление |
|
клапана |
1 |
смесь |
|
|
К |
|||
|
S |
|
Положение регулирующего |
Рис. 4.5 (П). Система регулирования кровяного давления
(б) Полагая D(s) = 0, определите установившуюся ошибку в случае линейного входного воздействия r{t) = t, t> 0.
(в) Выберите некоторое значение К < 10 и изобразите реакцию системы >(/) на единичное ступенчатое возмущение (считая r(t) = 0).
П-4.6. На рис. 4.6(П) изображена электрическая цепь с опережением по фазе, с которой мы встретимся в гл. 10.
|
£Z> R |
|
+ v |
(а) Определите передаточную функцию G(s) = Vn(s)/V(s).
|
R |
(б) Определите чувствительность G(s) по отношению к параметру С.
|
Рис. 4.6 (П). Цепь с опережением по фазе |
(в) Найдите и изобразите графически реакцию v0(<) на ступенчатое входное воздействие V(s) = 1/s.
П-4.7. На рис. 4.7(П) изображена структурная схема системы с обратной связью с учетом возмущения D(s) и шума датчика N(s). Необходимо уменьшить влияние шума и возмущения. Полагая R(s) = 0, определите:
(а) Влияние возмущения на выход системы Y{s);
(б) Влияние шума датчика на 7(s).
(в) Выберите наилучшее значение К из диапазона 1 < А'< 100. при котором влияние шума и возмущения на установившуюся ошибку будет минимальным. В данном случае примите D(s) = A/s и A'(s) = В/s.
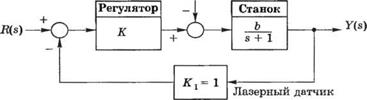
П-4.8. На рис. 4.8(П) изображена структурная схема системы управления рабочим органом станка.
(а) Определите передаточную функцию T(s) = Y(s)/R(s).
(б) Определите чувствительность S.
(в) Выберите К из диапазона 1 < К < 50, при котором влияние возмущения на 7(s) и чувствительность S будут минимальны.
|
Рис. 4.7 (П) Система при наличии шума |
|
.Y(s) |
|
О |
|
D(s) |
Объект |
|
|
Регулятор |
-1 |
управления |
|
к |
—о— |
2 |
|
S |
+ ^ |
s + 2 |
|
Возмущение |
|
Д( S)_^Q-^ |
|
Датчик |
|
*1-1 |
|
Шум N(s) датчика |
|
|
|
Рис. 4.8 (П) Система управления рабочим органом станка |
|
Щ s) |
Задачи на синтез систем
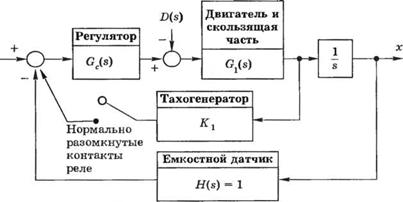
СС-4.1. В задаче СС-2.1 был описан привод скользящей части стола металлообрабатывающего станка. Положение скользящей части, х, измеряется с помощью емкостного датчика, как показано на рис. 4.1(СС), который обладает высокой точностью и линейной характеристикой. Изобразите модель системы с обратной связью и определите ее реакцию на ступенчатое входное воздействие в случае, когда H(s)= 1, а регулятор является обычным усилителем. Gc(s) = Ка. Решение получите для нескольких значений коэффициента Кя.
|
|
|
Рис. 4.1 (СС). Структурная схема системы с емкостным датчиком в цепи обратной связи. В системе дополнительно может быть использована тахометрическая обратная связь по скорости вращения электродвигателя (контакты реле являются нормально разомкнутыми) |
|
R(s) |
С-4.1. Замкнутая система управления скоростью подвержена влиянию возмущения по нагрузке, как показано на рис. 4.1(C). Заданное значение скорости со/г) =100 рад/с, а возмущение представлено единичной ступенькой, D(s) = І/s. При отсутствии нагрузки установившееся значение скорости равно 100 рад/с. (а) Определите влияние нагрузки в установившемся режиме и
(б) изобразите графически реакцию со(/) на ступенчатое возмущение при нескольких значениях коэффициента К из диапазона 10 < .К < 25. Установите наиболее подходящее значение коэффициента К.
|
|
|
c%(s) _ Заданная скорость |
|
Рис. 4.1 (С) Система управления скоростью |
|
Возмущение (нагрузка) D(s)
|
eo(s)
Действительная
скорость
С-4.2. Управление углом крена самолета осуществляется с помощью момента, создаваемого элеронами. На рис. 4.2(C) изображена линейная модель системы управления углом крена небольшого тренировочного самолета: на схеме системы q(l) есть поток жидкости, втекающей в гидроцилиндр, и
1
G(s) =
s~ + 4s + 9
Цель управления состоит в под держании небольшого угла крена 0, возникающего за счет действия возмущений. Полагая 0^/) = 0. выберите значение КК,. позволяющее снизить влияние возмущения и одновременно получить приемлемый вид переходного процесса, если возмущение имеет ступенчатый характер. Для получения желаемого вида переходного процесса задайтесь ограничением КК, < 35.
|
Td(s)
|
Рис. 4.2 (С)
|
0,00 |
Система управления углом крена самолета
|
(s + 5) |
|
|
|
w(s) Скорость |
|
|
|
Кл ----------------------------- ______________ Тахогенератор |
|
С-4.3. В систему управления скоростью на рис. 4.1(C) внесены изменения, так что теперь (б) Определите, при каких значениях К, и К в случае возмущения d(t) = 21 мрад/с. О < I < 5 с. Рис. 4.3 (С) Система скоростью to.(s) |
|
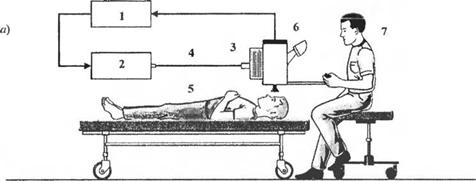
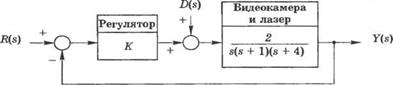
С-4.4. Уже более 25 лет в офтальмологии с успехом применяются лазеры. Они оказывают помощь при удалении части ткани или в процессе ее коагуляции. Лазер позволяет врачу-офтальмологу управляемым образом осуществлять локализованное тепловое воздействие на глаз пациента. Во многих процедурах мишенью лазера являє гея сетчатая оболочка глаза, которая тонким чувствительным слоем покрывает внутреннюю поверхность глазного яблока и преобразует световую энергию в электрические импульсы. Иногда сетчатка от слаивается от поверхности яблока, что приводит к потере ее кровоснабжения и, как следствие, к частичной или полной утрате зрения. В этом случае с помощью лазера можно «приварить» сетчатку на ее место на внутренней поверхности глазного яблока и восстановить зрение. Автоматическое управление положением луча лазера позволяет офтальмологу дать команду регулятору определить, где находится поврежденная ткань. Регулятор сканирует сетчатку и управляет положением лазера, наводя его точно на поврежденное место. Для определения смещения сетчатки используется широкоугольная видеокамера, как показано на рис. 4.4(C). Если глаз во время облучения совершает движение, то лазер должен либо быть переориентирован, либо выключен. На рис. 4.4(C). (б), приведена структурная схема управления положением лазера. Выберите подходящее значение коэффициента усиления регулятора. К, так, чтобы переходный процесс, вызванный ступенчатым изменением r(t), имел приемлемый характер, а влияние возмущения (шум системы) было бы минимальным. Убедитесь также, что при ступенча- |
|
|
|
|
|
Рис. 4.4 (С). Операционная система с использованием лазера; 1 — регулятор, 2 — аргоновый лазер, 3 — лазерная система, 4 — волоконно-оптическая линия, 5 — пациент, 6 — видеокамера, 7 — офтальмолог |
|
б) |
том изменении задания r(t) установившаяся ошибка будет равна нулю. Для получения приемлемого вида переходной характеристики воспользуйтесь ограничением К < 10.
С-4.5. Для генерирования коротких импуль
|
-о + |
|
ГК Рис. 4.5 (С). Схема на операционном усилителе |
|
сов специальной формы можно использовать схему на операционном усилителе. Схема, изображенная на рис. 4.5(C), при входном напряжении v(t) типа единичной ступеньки позволяет получить на выходе импульс v0(/) = Se'100*, t > 0. Предполагая, что операционный усилитель является идеальным, выберите соответствующие номиналы резисторов и конденсатора. |
Задачи, решаемые с помощью MATLAB
М-4.1. Разомкнутая система имеет передаточную функцию
G(s) = -7 .
s2 + 2s + 25
При единичном ступенчатом входном воздействии желаемое установившееся значение выходной переменной равно 1. С помощью функции step покажите, что установившаяся ошибка в этом случае равна 0,8.
М-4.2. Система с передаточной функцией G(s) = 50/s(s+l) охвачена единичной отрицательной обратной связью. С помощью MATLAB получите переходную характеристику системы и опре-
делите максимальное относительное перерегулирование. Чему равна установившаяся ошибка?
М-4.3. Система в замкнутом состоянии имеет передаточную функцию
TV л 10А'
T(s) = ~i----------- •
s +20s + К
Получите семейство переходных характеристик (при единичном ступенчатом воздействии) для К = 10, 100 и 500. Изобразите их на одном графике и оформите в виде таблицы основные результаты: относительное перерегулирование, время установления, установившуюся ошибку.
М-4.4. Рассмотрите замкнутую систему управления, изображенную на рис. 4.4(М). Подготовьте программу MATLAB, которая позволяла бы найти значение к. при котором относительное перерегулирование при единичном ступенчатом воздействии было бы более 1%, но менее 10%. Программа должна вычислять передаточную функцию замкнутой системы T(s) = Y(s)/R(s) и строить график переходной характеристики. По графику убедитесь, что установившаяся ошибка равна нулю.
|
Регулятор |
|
Объект |
|
10 S |
|
1 S + k |
|
Y(s) |
|
—О |
|
Рис. 4.4 (М) Система управления с отрицательной обратной связью |
М-4.5. На рис. 4.5(М) изображена замкнутая система управления. Регулятор имеет коэффициент усиления К = 2. Номинальное значение параметра объекта а = 1. Это значение принято только для решения задачи синтеза, т. к. действительное значение этого параметра точно не известно. В данной задаче целью исследований является определение чувствительности замкнутой системы к параметру а. (а) Полагая а = 1, покажите аналитически, что при единичном ступенчатом входном воздействии г(?) установившееся значение y(t) = 2. Убедитесь, что реакция на данное воздействие спустя 4 с отличается от установившегося значения не более чем на 2%.
(б) О чувствительности системы к изменению параметра а можно судить по виду переходной характеристики. Постройте графики этой характеристики при значениях а = 0,5: 2; 5 и сделайте соответствующие выводы.
|
Регулятор |
|
Объект |
|
R(s) |
|
О- |
|
К |
|
Рис. 4.5 (М) Замкнутая система управления с неопределенным параметром a |
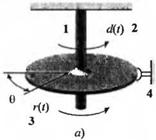
М-4.6. На рис. 4.6(М), (а), изображена механическая система с вращательным движением. У пругий момент, обусловленный скручиванием оси. равен —А0; момент трения, создаваемый тормозным устройством, равен —Ш. возмущающий момент равен d(t); входной момент равен г(1) момент инерции механической системы равен J. Передаточная функция данной системы имеет вид:
У J
G(s) = —z-----------------
s + (Ъ! J)s + к/ J
Замкнутая система управления механической системой изображена на рис. 4.6(М), (б). Для расчетов примите заданное значение угла 6rf= 0°, к = 5, b = 0,9 и J= 1.
(а) С помощью MATLAB, полагая r{t) = 0, определите реакцию 0(/) разомкнутой системы на единичное ступенчатое возмущение d(t).
|
|
|
|
|
б) |
|
Рис. 4.6 (М). (а) Механическая система с вращательным движением (1 — гибкая ось, 2 — возмущающий момент, 3 — входной момент, 4 — тормозное устройство); (6) Система с обратной связью, управляющая угловым положением механической системы |
|
d(t) |
(б) С помощью MATLAB, при коэффициенте усиления регулятора К0 = 50 определите реакцию 0(/) замкнутой системы на единичное ступенчатое возмущение d(t).
(в) Изобразите на одном графике две полученные кривые. Обсудите полученные результаты и сделайте вывод о преимуществах использования обратной связи для уменьшения влияния возмущения.
М-4.7. На рис. 4.7(М) изображена система управления с отрицательной обратной связью. Допустим, что целью синтеза является выбор регулятора Gc(s) минимальной сложности, причем система должна отрабатывать единичное ступенчатое входное воздействие с нулевой установившейся ошибкой.
(а) В качестве первой попытки рассмотрите простой пропорциональный регулятор Gc(s) = К, где К — фиксированный коэффициент усиления. Полагая К = 2. с помошью MATLAB постройте график реакции системы на единичную ступеньку и определите величину установившейся ошибки.
(б) Далее рассмотрите более сложный регулятор,
Cc(s)=KQ + ^1,
S
где К0 = 2 и К{ = 20. Такой регулятор известен под названием ПИ-регулятор (пропорционально-интегральный). Постройте график реакции системы на единичную ступеньку и определите величину установившейся ошибки.
(в) Сравните результаты пп. (а) и (б) и сделайте выводы относительно компромисса между сложностью регулятора и способностью систем минимизировать установившуюся ошибку.
|
R(s). |
|
о |
|
Y(s) |
|
Регулятор |
Объект |
|
|
GC(S) |
10 |
|
|
s + 10 |
Рис. 4.7 (М). Простая одноконтурная система управления
Ключевые термины и понятия
Замкнутая система. Система, в которой производится измерение выходного сигнала, сравнение его с желаемым значением и образование сигнала ошибки, воздействующего на исполнительное устройство.
Переходная характеристика. Реакция системы на входное воздействие как функция времени.
Разомкнутая система. Система без обратной связи, в которой выходной сигнал является непосредственной реакцией на входной сигнал.
Сигнал возмущения. Нежелательный входной сигнал, оказывающий влияние на выходной сигнал системы.
Сигнал ошибки. Разность между желаемым выходным сигналом R(s) и действительным выходным сигналом Y(s), т. е. £(.v) = R(s) - У(х).
Установившаяся ошибка. Ошибка, остающаяся спустя достаточно большой промежуток времени, достаточный для полного затухания переходного процесса.
Чувствительность системы. Отношение изменения передаточной функции системы к малому изменению передаточной функции (или параметра) объекта управления.