СОВРЕМЕННЫЕ СИСТЕМЫ УПРАВЛЕНИЯ
Пример построения диаграммы Боде
Диаграмма Боде для передаточной функции G(s), содержащий несколько нулей и полюсов, строится путём суммирования частотных характеристик, соответствующих каждому отдельно взятому полюсу и нулю. Простоту и удобство данного метода мы проиллюстрируем на примере передаточной функции, включающей в себя все сомножители, рассмотренные в предыдущем разделе. Эта передаточная функция имеет следующий вид:
|
(8-42) |
5(1 + у'ОДсо)
С(ую) = -
ую(1 + у'0,5юХ1 + у'0,6(со/50)+(ую/50)2]
Расположим эти сомножители в порядке начала их влияния с ростом частоты: 1- Постоянный коэффициент усиления К = 5;
2. Полюс в начале координат;
3. Полюс при са=2;
4- Нуль при со = 10;
|
|
|
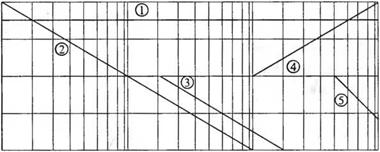
Рис. 8.19. Асимптотические амплитудные характеристики для отдельных сомножителей функции G(/m) вида (8.42) |
|
п € о |
5. Пара комплексно-сопряжённых полюсов при со = сои = 50.
Сначала мы изобразим амплитудные характеристики, соответствующие каждому полюсу и нулю и постоянному коэффициенту усиления.
1. Коэффициенту усиления соответствует логарифмическая амплитудная характеристика 20 lg5 = 14 дБ, как показано на рис. 8.19.
2. Амплитудная характеристика, соответствующая полюсу в начале координат, при всех частотах от 0 до оо имеет вид прямой с наклоном -20 дБ/дек, пересекающей уровень 0 дБ в точке со = 1, как показано на рис. 8.19.
3. Амплитудную характеристику, соответствующую полюсу при со = 2, аппроксимируем двумя асимптотами. Высокочастотная асимптота справа от точки излома со = 2 имеет наклон — 20 дБ/дек, а низкочастотная (слева от точки излома ) проходит на уровне 0 дБ (см. рис. 8.19).
4. Нулю при со = 10 также сопоставим две асимптоты, из которых высокочастотная (правее точки излома) имеет наклон +20 дБ/дек (см. рис. 8.19).
5. Наконец, если воспользоваться асимптотами для построения амплитудной характеристики, соответствующей паре комплексных полюсов, то точка излома будет иметь место на частоте со = со„ = 50, а наклон высокочастотной асимптоты составит -40 дБ/дек в силу наличия в сомножителе квадратичного члена (см. рис. 8.19). Однако при коэффициенте затухания С, = 0,3 точная амплитудная характеристика существенно отличается от асимптотической, поэтому в построение необходимо внести поправки, как это сделано на рис. 8.20.
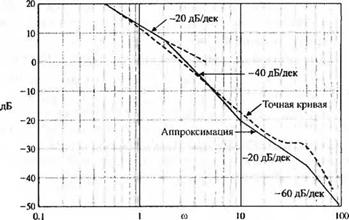
Таким образом, результирующая асимптотическая амплитудная характеристика изображается путём суммирования асимптот, соответствующих каждому сомножителю передаточной функции, как показано сплошной линией на рис. 8.20. Анализ рис. 8.20 показывает, что эта характеристика может быть получена непосредственно путём добавления каждой асимптоты в порядке возрастания частоты. Так, прямая с наклоном -20 дБ/дек, соответствующая члену (/со)-1, пересекает уровень 14 дБ при (0=1. Далее, при со = 2 наклон изменяется до - 40 дБ/дек за счёт полюса и снова становится равным -20 дБ/дек за счёт нуля при со = 10. Наконец, при со = 50 наклон становится равным -60 дБ/дек из-за пары комплексных полюсов.
Рис. 8.20
|
|
Амплитудная
характеристика
Точную амплитудную характеристику можно получить, воспользовавшись данными табл. 8.2, где приведены расхождения между точной и асимптотической характеристикой, соответствующими единственному полюсу или нулю. Что касается точной амплитудной характеристики, соответствующей паре комплексных полюсов, то для её изображения следует воспользоваться кривыми на рис. 8.10(a). Точная характеристика для функции G(jiо) показана на рис. 8.20 пунктирной линией.
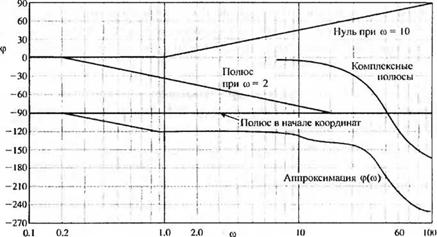
Фазовую частотную характеристику можно построить точно так же, суммируя соответствующие кривые для каждого отдельного сомножителя. Для единственного полюса или нуля в качестве первого приближения обычно бывает достаточно линейной аппроксимации фазовой характеристики. Такая аппроксимация изображена на рис. 8.21.
1- Для постоянного коэффициента усиления фазовая характеристика равна 0°.
2. Полюсу в начале координат соответствует фазовый сдвиг -90°.
3. Для полюса при ю = 2 на рис. 8.21 приведена соответствующая линейная аппроксимация фазовой характеристики, причём на частоте со = 2 фазовый сдвиг равен - 45°.
|
Рис. 8.21. Фазовая характеристика |
4. Для нуля при ю = 10 на рис. 8.21 также приведена линейная аппроксимация фазовой характеристики, и на частоте со = 10 фазовый сдвиг равен +45°.
5. Действительная фазовая характеристика, соответствующая паре комплексных полюсов, заимствованная с рис. 8.10(6), также приведена на рис. 8.21.
Таким образом, результирующая фазовая характеристика ср(со) получается простым сложением характеристик, соответствующих каждому сомножителю передаточной функции, как показано на рис. 8.21. Поскольку полученная зависимость является лишь аппроксимацией истиной характеристики, её следует рассматривать только в качестве первого приближения. Например, как мы увидим ниже, особый интерес представляет частота, при которой ф(ю) = - 180°. Аппроксимация показывает, что ср(со) = - 180° на частоте со = 46. Попробуем вычислить действительный фазовый сдвиг при со = 46:
ILu
ф(со) = -90° - arctg(0T[ +arctg(ot2 - arctg , (8.43)
1- и"
где т, = 0,5 ; т2 = 0,1 ; и - со/ю„ = ю/50. Вычисления дают результат:
ф(46) = - 90° - arctg 23 + arctg 4,6 - arctg 3,55 = - 175°, (8.44)
т. е. аппроксимация фазовой характеристики при со = 46 даёт ошибку в 5°. Однако всегда имеется возможность, определив интересующую частоту по аппроксимирующей характеристике, уточнить её значение в окрестности найденной точки с помощью выражения (8.43). Этот метод обычно является предпочтительным при вычислении точного значения фазового сдвига в пределах нескольких декад. Наконец, с помощью линейной аппроксимации амплитудной и фазовой характеристик можно установить диапазон частот, представляющий интерес для анализа свойств системы с передаточной функцией G(ja). После этого в данном диапазоне всегда можно вычислить действительные значения частотных характеристик, пользуясь их точными уравнениями, такими как, например, (8.43).
|
|
|
Max. mag = 33.96906 dB Max. phase = -92.35844 deg The gain is 2500 |
|
Min. mag = -112.0231 dB Min. phase = -268.7353 deg |
|
0.1 1 10 100 1000 Частота, рад/с |
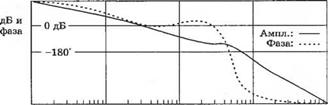
Частотные характеристики, соответствующие функции С(/со), легко можно вычислить и изобразить графически с помощью компьютера, например, в среде MATLAB. Для примера, рассмотренного в данном разделе, построенная таким образом диаграмма Боде приведена на рис. 8.22. Диаграмма занимает 4 декады, на ней указаны уровни 0 дБ для амплитудной характеристики и -180° — для фазовой. Данные над диаграммой показывают, что при со = 0,1 амплитудная и фазовая характеристики соответственно равны 34 дБ и -92,36°. По выводимым табличным данным можно также найти, что 20 lg|G(/co)| = 0 дБ при со = 3, а ф(ю) = -180° при ю = 50.
Рис. 8.22
Диаграмма Боде для Gfja) вида (8.42)