СОВРЕМЕННЫЕ СИСТЕМЫ УПРАВЛЕНИЯ
Графики частотных характеристик
Передаточную функцию системы G(s) можно представить в частотной области с помощью соотношения
G(yco) = С(л-)|,=,(11 = R( со) + jX (со), (8.8)
где R(со) = Re[G(/co)] и Л"(со) = Im[G(/co)].
Иным способом то же выражение можно представить как
С(/со) = |G(/to)|ew"n), (8.9)
где
ф(со) = aictg и |G(/co)|2 = R2(со) + X2(co).
R( со)
|
Іт(С)=Х(ш) |
|
Re(G)=R(co) |
|
О |
Для графического изображения частотных характеристик можно воспользоваться выражениями (8.8) или (8.9). Выражение (8.8) позволяет представить частотные характеристики в полярных координатах (на комплексной плоскости), где изображаются действительная и мнимая части G(ju>), как показано на рис. 8.1. Проиллюстрируем
сказанное на простом примере. Рис - 81 ■ Комплексная плоскость
Пример 8.1. Частотные характеристики RC-фильтра
+ °------------ 1— ■ - і--------------------------- ° + На рис. 8.2 изображён простейший ЛС-фильтр. Пере-
^ даточная функция фильтра имеет вид
|
(8.10) |
|
F,(s) RCs+1 а его частотная функция соответственно равна G(» =------------------- =------- J----- . MRC)+ j( co/co,)+1 |
Vfc) С_,_ V2(s) _ V3(S) 1
|
(В. 11) |
Рис. 8.2. RC-фильтр
|
(8.12) |
|
С (jw) = R{со) + jX (со) = |
|
1+ (со/со,) |
|
где со, = 1 IRC.. Тогда это выражение можно представить следующим образом: 1- j(w/co,) 1 |
|
1+ (со/со,)2 J 1+ (со/со,)2 |
|
со/со, |
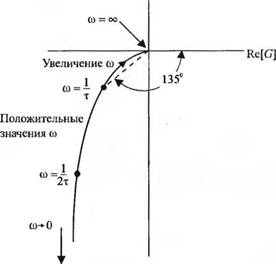
Сначала определим R{со) иХ(со) при двух частотах, со = 0 и ш = оо. При со = 0 мы имеем R(со) = 1 иДш) = 0, а при со = то У?(со) = 0 иХ(о>) = 0. Эти две точки показаны на рис. 8.3. Г одограф векто-
Рис. 8.3
|
Отрицательные значения со |
|
Х{ы) |
Частотная характеристика RC-фильтра в полярных координатах
|
‘,1 |
|
/ |
|
со = О |
|
ев = со, Положительные значения со |
|
|
-R( со)
pa G(Jсо) также изображён на рис. 8.3 и легко можно показать, что он представляет собой полуокружность с центром в точке (1/2,0 ). При to = ш, действительная и мнимая части (/(/со) равны и угол ф(со) = — 45°. Функцию G(/co) можно представить в виде
G(/co) = |G(/co)| еМш (8.13)
где
1
|
|СО'со)| = - |
и ф(со) = - arctg (со/со,).
д/і+ (со / со,)2
Таким образом, при со = со, |G(jco,)| = 1/V2 и ф(со,) = - 45°. Кроме того, при со —> оо мы имеем | G(/co) | -» 0 и ф(со) = - 90°. Аналогично, при со = 0 |G(/co)| = 1 и ф(со) = 0.
Пример 8.2. Изображение передаточной функции в полярных координатах
Представление передаточной функции в полярных координатах полезно при анализе устойчивости систем, как это будет рассмотрено в главе 9. Поэтому здесь уместно привести ещё один пример. Рассмотрим передаточную функцию
К К
(8.14)
G(i’)L«=/m = G(jco) =
усо(JCOT +1) Jсо - со т
|
(і)- |
Тогда выражения для её модуля и аргумента будут иметь вид:
|
|G(»|= |
К
и ф(со) = - arctg
л/со2 + coV
По этим выражениям легко вычислить аргумент и модуль функции G(/co) при частотах со = 0, со = 1/т и со = оо. Эти значения приведены в табл. 8.1, а график G(/co) в полярных координатах изображен на рис. 8.4.
|
Таблица 8.1
|
Альтернативным способом является использование действительной и мнимой частей функции GO'co):
|
К jm - со2т |
|
(8.15) |
|
G(» = - |
|
= Л(со) + jX (со) , |
|
К (-./со - со т) |
|
|
|
Im[G] |
|
Рис. 8.4. Частотная характеристика Рис. 8.5. Вычисление G(jo-) по двум G(/w) = + 1) в полярных координатах векторам на s-плоскости |
|
j®
|
где /<’(со) = - К со"т/А/(со) и ATto) = — со К / М((о), при обозначении М(со) = со" + to4 т". Тогда при со =0 мы имеем Л(со) = - Ат иТ(о) = —оо, а при со = оэ соответственно Л(со) = 0 иДи) = 0. Если о = 1/т, то А(ю) = Дев) = - Ат/2, как показано на рис. 8.4.
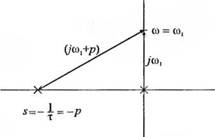
Другой метод предполагает графическое определение вектора G(/co) при разных частотах ы. т. е. фактически при изменении переменной s вдоль мнимой оси. s =ja>. Рассмотрим функцию
К/т
G(*) =
s(s+ 1/т)
и отметим на ^-плоскости два её полюса, как это показано нарис. 8.5. Тогда при s =7 со мы получим
К/х
С (./со) =
гдер= 1/т. Модуль и аргумент С(/со) при частоте со, можно определить с помощью рис. 8.5:
|С(>.)1=7Т-Т ------------ ,
|jco,||;co, + p|
и argG(/co,) = cp(coj) = - aigO'co,) - arg(/co, + p) = - 90е - arctg(co,/p).
Частотные характеристики системы могут быть графически изображены в разных координатах. Как только что было показано, это можно сделать в полярных координатах (на комплексной плоскости) с использованием выражения (8.8). Однако сразу же обнаруживается недостаток этого метода. При добавлении в передаточную функцию полюсов или нулей частотные характеристики системы надо вычислять заново, как нетрудно видеть из примеров 8.1 и 8.2 (см. табл. 8.1). К тому же вычисление частотных характеристик подобным методом представляет собой трудоёмкую процедуру и не позволяет оценить влияние на их вид отдельных полюсов или нулей.
Решение задачи существенно упрощается при использовании логарифмических частотных характеристик, часто называемых диаграммами Боде. Последнее название обязано своим происхождением X. У. Боде, который широко использовал логарифмические характеристики при исследовании усилителей с обратной связью. Передаточная функция системы в частотной области имеет вид:
СО) = |G(/co)| е^ (8.16)
Усиление системы обычно характеризуется десятичным логарифмом модуля G(j со) и измеряется в децибелах (дБ):
Коэффициент усиления = 20 lg |G(yco)| . (8.17)
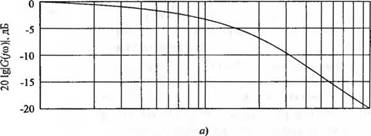
Амплитудно-частотную характеристику, выраженную в децибелах, и фазовую частотную характеристику ф(со) обычно изображают на отдельных графиках, как показано на рис. 8.6.
В качестве иллюстрации построим диаграмму Боде, соответствующую передаточной функции из примера 8.1.
Пример 8.3. Диаграмма Боде для /?С-фильтра
Напомним передаточную функцию из примера 8.1:
|
(8.18) |
1 1
С(» =
jwRC + 1 j'cot + Г
|
(8.19) |
|
20Ig|G(yco)|= 201g |
|
(8.20) |
|
■ 1+ (ют)' При малых частотах, т. е. при со 1/т мы имеем: 20 lg|G(/co)| ю - 10 lgl = 0 дБ, со « 1/т. |
|
где т = RC есть постоянная времени фильтра. Коэффициент усиления равен -11/2 |
|
= — 1 Olgf 1 ч - (сот) ]. |
|
1 |
|
|
|
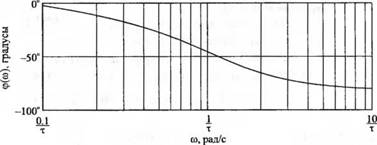
Рис. 8.6 Диаграмма Боде для функции G(/cd) = = 1/(M + 1): (а) амплитудная характеристика и (б) фазовая характеристика |
|
б) |
При больших частотах, т. е. при to » 1/т получим
|
(8.21) |
20 lg|G(/co)| к - 20 lg сот, со » 1/т. а на частоте со = 1/т
20 lg|G(/co)| = - 10 lg 2 = - 3,01 дБ.
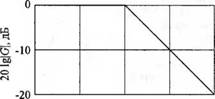
Амплитудная характеристика фильтра изображена на рис. 8.6(a). Фазовая характеристика фильтра определяется выражением
ф(ю) = - arctg сот (8.22)
и изображена на рис. 8.6(6). Частоту со = 1/т принято называть частотой излома или сопрягающей частотой.
Линейный масштаб для частоты является не слишком удобным, поэтому предпочтительнее использовать логарифмический масштаб. О его преимуществе можно судить по выражению (8.21), которое при со » 1/т выглядит как
20 lg|G(/co)| = - 201g сот = - 20 lgx - 20 lgco. (8.23)
Тогда, если по оси абсцисс откладывать lgco, то при со » 1/т асимптотой амплитудной характеристики будет прямая линия, как показано на рис. 8.7. Наклон этой прямой линии можно установить по выражению (8.21). Расстояние между двумя частотами, отличающимися в 10 раз, например, между со, и со2, где со2 = 10 со,, называется декадой. При частотах со » 1/т изменение амплитудной характеристики при изменении частоты на декаду составляет
201g|G(y'co, )| -201g|G(y'co2 )| =-201gco1T-(-201gco2x) =
|
(8.24) |
|
= +20 дБ. |
= -201g^=-201gfi - со2т V10
|
|
|
1 Ют |
|
1 т со |
Таким образом, для данной передаточной функции первого порядка наклон высокочастотной асимптоты амплитудной характеристики равен - 20 дБ/дек, как показано на рис. 8.7.
Вместо использования прямоугольной сетки ко-
|
Рис 8.7. Асимптотическая характеристика для (/ют + 1)-1 |
lgco, проще изображать амплитудную характеристику в полулогарифмическом масштабе с равномерной разметкой оси ординат в децибелах и логарифмической разметкой оси со. Можно было бы также использовать логарифмическую раз - метку оси ординат, избегая тем самым необходимости вычисления lg |G(/co)|.
Иногда используют интервал частот, при котором крайние частоты отличаются в 2 раза, т. е.
со2 = 2со,. Такой интервал называют октавой. При частотах со » 1/т изменение амплитудной характеристики при изменении частоты на октаву составит

|
= 6,02 дБ, |
|
(8.25) |
201g|GOco, )| - 201g|G(yco, )| = -20lg ^ = -201g( -
со, т V 2
что эквивалентно наклону асимптоты, равному - 20 дБ/дек.
Основное преимущество логарифмических частотных характеристик состоит в том, что сомножители вида (/ют + 1), входящие в передаточную функцию, при построении учитываются в виде суммы членов 201g Ij'Cot + 1|. Это легко проиллюстрировать, если рассмотреть передаточную функцию общего вида:
х4П(1+/“т|)
|
(8.26) |
/=1
G(» = -
м
)2]
|
!(йг |
0'Ш)Л П(1+/-га)П[1+ (2^/fl4 )>+ (jafi
т=1 А=1
Эта передаточная функция имеет g нулей, N полюсов в начале координат, М полюсов на действительной оси и R пар комплексно-сопряжённых полюсов. Для такой функции построение частотных характеристик в полярных координатах было бы чрезвычайно затруднительным. В логарифмическом же масштабе для амплитудной характеристики мы получим:
и
201g|G(/o>)| = 201g*4 +£201g|l + 7COT(|-201g|(»w |-
/= 1
|
/ - /ю V У |
|
(8.27) |
|
1 + |
|
;ю+ |
|
(0„ V "* / |
|
-Х201Е|1 + 7штт|-Е201е т=1 *=1 |
|
м |
и диаграмма Боде легко получается путём сложения характеристик, соответствующих каждому отдельному сомножителю. Аналогичным образом, фазовая частотная характеристика получается сложением соответствующих характеристик отдельных сомножителей:
|
м |
|
(8.28) |
|
1-(ы/ш )- |
|
cp(o) = £arctg сот,-N(90°) - 5]arctg сот,,, - £arctg /=1 1Я=1 £ = 1 |
|
2С* (“/ю,, ) |
Итак, передаточная функция может содержать четыре разного вида сомножители:
1. Постоянный коэффициент усиления Кь.
2. Полюсы (или нули) в начале координат (/со).
3. Полюсы (или нули) на действительной оси (/ют +1).
4. Комплексно-сопряжённые полюсы (или нули) [1 + (2£/ю„) у'ео + (/to/co,,)2].
Для каждого из этих сомножителей можно найти вид амплитудной и фазовой частотных характеристик и затем использовать их для построения диаграммы Боде, соответствующей передаточной функции общего вида. Эти характеристики, вообще говоря, являются криволинейными, однако процедуру построения диаграммы Боде можно упростить, если воспользоваться их аппроксимацией асимптотами, а точные значения получать только при отдельных частотах, представляюших особый интерес.
Постоянный коэффициент усиления Кь. Логарифмическая амплитудная характеристика определяется выражением
201g Кь = const, дБ,
а фазовая характеристика
ф(со) = 0.
На диаграмме Боде амплитудная характеристика изображается просто в виде горизонтальной линии.
Если коэффициент усиления является отрицательным, т. е. - Кь, то логарифмическая амплитудная характеристика по-прежнему равна 201gKh, а знак минус учитывается сдвигом по фазе на — 180°.
|
(8.29) |
Полюсы (или нули) в начале координат (/со). Полюсу в начале координат соответствует логарифмическая амплитудная характеристика
|
20 lg |
1 |
= -20lgco, дБ, |
|
усо |
а фазовая характеристика
ф(ш) = - 90°.
|
(8.30) |
Как видно из (8.29), амплитудная характеристика имеет вид прямой линии с наклоном-20 дБ/дек. Аналогично, если в начале координат находится полюс кратности N, то
|
1 |
||
|
20 lg |
= -20N lg со |
|
|
0<o)N |
ф(ш) = - N ■ 90°.
|
(8.31) |
В этом случае наклон логарифмической амплитудной характеристики равен -20 N дБ/дек. Если в начале координат находится нуль передаточной функции, то мы имеем:
20 lg|/co| = + 20 lgco,
что соответствует уравнению прямой с наклоном + 20 дБ/дек. Фазовая характеристика
ф(со) = + 90°.
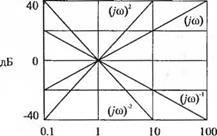
Диаграммы Боде, соответствующие функции (/со)1 N, изображены на рис. 8.8 для N = 1 и N=2.
|
180 |
|
|
3 |
90 |
|
О |
|
|
Я |
|
|
& |
0 |
|
3^ 'e- |
-90 |
|
-180 |
|
(juf (Ja>) Ы №' |
|
|
|
(/со)2 |
|
0.1 |
|
10 |
|
100 |
Рис. 8.8. Диаграммы Боде для (/w)±/v
Полюсы или нули на действительной оси. Наличие полюса на действительной
|
(8.32) |
оси обусловлено сомножителем вида ( 1 + у'сот)-1, и этот случай уже был нами рассмотрен. Напомним, что амплитудная характеристика определяется уравнением
|
20 lg |
1 |
- 101g(l+coV). |
|
1 + уют |
||
Прямолинейные асимптоты имеют следующие уравнения: при со <к 1/т 201gl = 0 дБ и при ю » 1/т -201g сот, что соответствует наклону -20 дБ/дек. Две асимптоты пересекаются в точке, определяемой уравнением
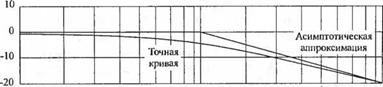
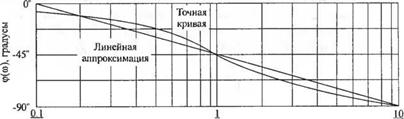
20 lg 1 = 0 дБ = -20 lgcoT, т. е. при со = 1/т, называемой частотой излома. Точное значение амплитудной характеристики при со = 1/т равно -3 дБ. Фазовая характеристика имеет уравнение ф(со) = - arctg сот, а диаграмма Боде для сомножителя (1 + усот)- представлена на рис. 8.9.
Диаграмма Боде, соответствующая нулю передаточной функции, т. е. сомножителю (1 + усот), получается аналогичным образом с той лишь разницей, что наклон высокочастотной асимптоты амплитудной характеристики равен + 20 дБ/дек, а ф(со) = + arctg сот.
На рис. 8.9 приведена также линейная аппроксимация фазовой частотной характеристики, которая совпадает с точной характеристикой на частоте излома, а при всех остальных частотах отличается о неё не более, чем на 6°. Подобная аппроксимация может оказаться полезной для предварительного суждения о фазовой характеристике системы с передаточной функцией G(s). Однако часто необходимо иметь точный вид фазовой характеристики, поэтому для сомножителей первого порядка соответствующие кривые можно вычислить на компьютере, скажем, с помощью простой программы MATLAB. В табл. 8.2 приведены точные значения частотных характеристик, соответствующих полюсу передаточной функции, т. е. члену (1 + уют)-1, а также для сравнения даны значения, полученные при аппроксимации характеристик прямолинейными отрезками.
|
|
о)
|
|
|
б) |
|
Рис. 8.9. Диаграмма Боде для функции (1 + ушт) 1 |
|
Таблица 8.2
|
Комплексно-сопряжённые полюсы или нули [1 + (2£/юп) 7'со + (/ю/ю„)-]. Квадратичный член, соответствующий паре комплексно-сопряжённых полюсов, можно представить в виде
[1 +у2С и - и2]~ (8.33)
где и = ю/юп. Тогда для пары комплексно-сопряжённых полюсов логарифмическую амплитудную характеристику можно представить в виде
|
(8.34) |
|
201g |G(/co)| |
10 lg [(1 - и2)2 + 4CV] ,
а фазовую характеристику в виде
|
2fyi |
|
(8.35) |
cp(co) = - arctg
Если и<к 1, то
201g |G(/co)| = - 10 lgl = 0 дБ,
а фазовая частотная характеристика близка к 0°. Если и »1, то логарифмическая амплитудная характеристика
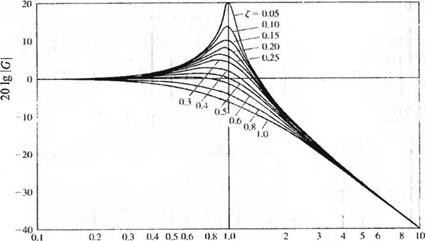
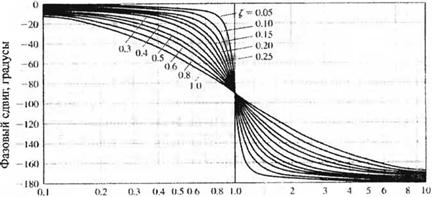
20 lg |G(/to)| « - 10 lgM4 = - 40 lgw, что соответствует наклону - 40 дБ/дек. При и »1 фазовая характеристика стремится к значению -180°. Асимптоты амплитудной характеристики пересекаются при значении 0 дБ, если и = ю/ш„ = 1. Однако расхождение между точной амплитудной характеристикой и её аппроксимацией зависит от коэффициента затухания и принципиально должно учитываться при С, < 0,707. Диаграмма Боде, соответствующая квадратичному члену в передаточной функции, изображена на рис. 8.10. Максимальное значение амплитудной характеристики, имеет место на резонансной частоте юг Если коэффициент затухания стремится к нулю, то сог—> со„, что соответствует частоте колебаний при отсутствии затухания. Резонансная частота определяется путём приравнивания нулю производной от выражения (8.33) по нормированной частоте и. Таким образом, резонансная частота определяется выражением
С, < 0,707,
|
(8.36) |
|
со. |
= «Jl-2C2.
|
(8.37) |
|
£ < 0,707, |
|
МРю =|G(7«Dr)| = (2cVi |
а максимальное значение | G(/co) | равно
|
ч = а>! со„ = Относительная частота |
|
Рис. 8.10. Диаграмма Боде для функции G(/u>) = [1 + (2tjan)j<a + (/co/to,,)2]-1 |
в случае пары комплексно-сопряженных полюсов. На рис. 8.11 приведена зависимость максимума амплитудно-частотной характеристики и резонансной частоты шг от коэффициента затухания С,, соответствующего паре комплексно-сопряженных полюсов. В предположении, что пара комплексно-сопряженных полюсов является доминирующей для замкнутой системы, эти кривые могут служить средством оценки качества системы по её частотным характеристикам, определённым в результате эксперимента.
Частотные характеристики можно получить также из геометрических соображений путём определения модулей и аргументов векторов, проведенных на s-плоскости из полюсов передаточной функции в точку на мнимой оси s=ja, при изменении со от 0 до со.
Рассмотрим, например, передаточную функцию второго порядка с комплексно-со
пряжёнными полюсами
G(s) =----------- —!--------------- =- ^(8.38)
(.s/ «ал) + 2<^/ oj„ +1 s + 2 С, а„ s + ш„
|
Рис. 8.11 Зависимость максимума амплитудной характеристики Мр и резонансной частоты cv от параметра С,, соответствующая паре комплексносопряженных полюсов |
|
1.0 |
|
м. |
|
1.0 |
|
0.10 |
|
0.20 |
|
ч |
N |
|||||||||||||||||||||||
|
ч |
N |
|||||||||||||||||||||||
|
N |
||||||||||||||||||||||||
|
X |
СО/СО,, |
|||||||||||||||||||||||
|
N |
s |
|||||||||||||||||||||||
|
S |
||||||||||||||||||||||||
|
s |
||||||||||||||||||||||||
|
N |
||||||||||||||||||||||||
|
1 |
||||||||||||||||||||||||
|
V |
||||||||||||||||||||||||
|
V |
||||||||||||||||||||||||
|
м |
||||||||||||||||||||||||
|
N |
||||||||||||||||||||||||
|
S. |
||||||||||||||||||||||||
|
ч |
||||||||||||||||||||||||
|
Ч |
||||||||||||||||||||||||
|
3.0 |
|
2.75 |
|
2.5 |
|
2.25 |
|
2.0 |
|
1.75 |
|
1.5 |
|
1.25 |
|
0.30 |
|
0.40 |
|
0.50 |
|
0.60 |
|
0.90 |
|
0.80 |
|
0.70 |
|
0.60 |
|
0.50 |
|
0.40 |
|
0.30 |
|
0.20 |
|
0.70 |
|
3.25 |
|
{ |
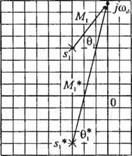
Полюсы располагаются на окружности радиуса со„; в частном случае, при определённом значении £ их положение указано на рис. 8.12 (я). Произведя замену s = у'ю, запишем передаточную функцию в виде
|
со: |
|
(8.39) |
С(» = -
(S-Sl )(s-s, )
где Sj и — комплексно-сопряжённые полюсы. На рис. 8.12(g) показаны также векторы (/о - s'i) и (J co-s,), проведённые из полюсов в точкуу'ю. Тогда, задавая различные значения частоты, можно определить модуль и аргумент функции G(/co):
со:
|
(8.40) |
|С(»|=-
І7С0-5, Ц/ш-Sj |
|
е, |
||||||||||
|
Л1 |
-А |
Л; |
7 |
-j |
со,. |
|||||
|
М |
/ |
|||||||||
|
'/ |
||||||||||
|
0 |
||||||||||
|
Г |
||||||||||
|
L |
Г |
|||||||||
|
Л |
||||||||||
|
s |
ч і |
|
в) |
|
|
|
V |
.. е |
|||||||||
|
V |
||||||||||
|
Ь |
{к |
|||||||||
|
М |
||||||||||
|
м* |
/ |
0 |
||||||||
|
/ |
||||||||||
|
/ |
||||||||||
|
* S |
/ |
0 |
||||||||
|
1 1 |
|
1 |
||||||||||
|
•>1 / |
Ч |
ч |
||||||||
|
( |
£0-5 і СО - S, |
,) |
ч |
|||||||
|
/ |
||||||||||
|
(/ |
*) |
/ |
||||||||
|
/ |
0 |
|||||||||
|
і |
||||||||||
|
/ |
||||||||||
|
/ |
||||||||||
|
si |
|
Рис. 8.12 Вычисление частотных характеристик с помощью векторов для некоторых значений о |
|
а) б) |
<p(co) = - arg(/ow, )-arg(/M-s1 ).
На рис. 8.12 (б, в, г) соответственно показано, как определяются эти характеристики для трёх конкретных значений частоты: со = 0, со = сог и со = со^. Соответствующие этим частотам значения амплитудной и фазовой характеристик показаны на рис. 8.13.

|
ф(оо) |
|
|С| |
Рис. 8.13
Частотные характеристики, соответствующие паре комплексно-сопряженных полюсов
90”
|
"1 |
|||||||||||||||||||
|
/ |
s |
Iі |
J 1 |
||||||||||||||||
|
Vj |
|||||||||||||||||||
|
N |
Ч |
||||||||||||||||||
|
ч |
. |
к |
|||||||||||||||||
|
ч |
ср(ы) |
Ч |
|||||||||||||||||
|
ч |
ч |
S |
|||||||||||||||||
|
ч |
|||||||||||||||||||
|
1,5 Мп. |
|
1.0 |
|
0.5 |
|
-90 |
|
-180“ |
0.0
Пример 8.4. Диаграмма Боде двойного Т-образного фильтра
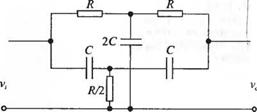
В качестве примера определения частотных характеристик, основанного на расположении полюсов и нулей передаточной функции и использовании векторов, направленных к точке /со, рассмотрим двойной Т-образный фильтр, изображённый на рис. 8.14. Передаточная функция этого фильтра имеет вид:
|
+ о- |
|
о + |
|
(sx)2 + I |
|
|
|
K(s) (sz)~ + 4 st + 1 где t = RC. Нули этой функции на плоскости переменной sx расположены в точках +_/!. а полюсы — в точках -2± -/З, как показано на рис. 8.15(a). При to = 0 мы имеем |G(/co)| = 1 и ф(со) = 0°. При to = 1/х |G(/o))| = 0, а аргумент вектора, начало которого находится в нуле sx =jl, при прохождении 7(ох через эту точку претерпевает скачок на 180°. При to -»°о |G(/'co)| = 1 и ф(со) = 0°. Произведя вычисления при нескольких промежуточных значениях частоты, нетрудно убедиться, что частотные характеристики будут иметь вид, изображённый на рис. 8.15(6). В табл. 8.3 приведены асимптотические частотные характеристики для основных типовых сомножителей, входящих в передаточные функции. В предыдущих примерах полюсы и нули функции G(s) были ограничены принадлежностью к левой полуплоскости. Однако система может иметь нули, расположенные в правой половине 5-ПЛОСКОСТИ и при этом быть устойчивой. Передаточные функции, нули которых расположены в правой полуплоскости, классифицируются как создающие неминимальный фазовый сдвиг. Если нули двух передаточных функций расположены симметрично относительно мнимой оси, то этим функциям соответствуют одинаковые амплитудные характеристики, а отличаются они только фазовыми характеристиками. Если сравнить фазовые характеристики двух этих систем, то легко можно увидеть, что при изменении частоты от 0 до оо система, все нули которой находятся в левой полуплоскости, будет давать меньший фазовый сдвиг. Поэтому передаточная функция G^s), все 1 |
|
Рис. 8.14 Двойной Т-образный фильтр |
|
jax 6 Л |
|
G(s) = |
|
|С| |
|
S1 - плоскость |
|
-J_______ I— |
|
V0(s) . |
|
(8.41) |
|
ОТ |
|
1/т |
|
-2+V3 |
-2-V3 -2
|
Г |
90"
|
I |
||||||||||
|
1 1 |
||||||||||
|
1 1 |
||||||||||
|
1 |
||||||||||
|
1 |
||||||||||
|
1 |
|
ф(ш) 0° |
-90
|
б) |
а)
Рис. 8.15. Двойной Т-образный фильтр: (а) расположение полюсов и нулей и (б) частотные характеристики
Таблица 8.3. Асимптотические частотные характеристики
для основных сомножителей передаточных функций
|
Сомножитель |
Амплитудная характеристика, 20 lg |(7) Фазовая характеристика, ф((о)
|
90' 45‘ (р((о) 0 -45‘ -90'
90‘ 45е ф(ш) 0 |
|
40 20 20 lg К |
|
дБ |
|
0 -20 -40 40 20 0 -20 -40 |
|
дБ |
|
0.ІШ, |
|
10(о, |
|
40 20 0 -20 -40 |
|
дБ |
|
-45‘ -90' 90’ 45' <р(£о) 0 -45° |
|
0.1(0, (о, |
|
10(о, |
|
|
|
40 20 0 -20 -40 |
|
0.01 0.1 |
|
10 |
|
100 |
|
-90°1— 001 |
|
0 I |
|
10 |
|
100 |
|
5. Два комплексных полюса, 0.1<С<1,С(/ю)= и=ы/ш„ |
|
4. Полюс в начале координат, G(/to)=l//ci) |
|
дБ |
|
3. Полюс, СЦы)= (1+Усо/со,) ' |
|
2. Нуль, G(/to)= (l+y'co/co,) |
|
1. Константа, G(j<a)=K |
|
0.1(0, (о, 10(0, (о |
нули которой расположены в левой полуплоскости, называется минимально-фазовой. В свою очередь, передаточная функция G2(s), удовлетворяющая условию | С,(/ы)| = |d7,(/co)f, но все нули которой расположены в правой полуплоскости симметрично нулям G^s) относительно мнимой оси, называется неминимально-фазовой.
Передаточная функция называется минимально-фазовой, если все её нули расположены в левой половине s-плоскости. Если передаточная функция имеет нули в правой полуплоскости, то она называется неминимально-фазовой.
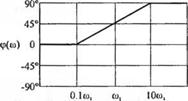
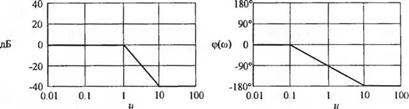
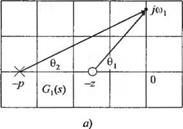
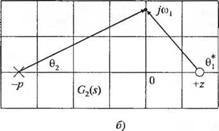
На рис. 8.16 (а) и (б) показаны расположения полюса и нуля, которым соответствует одинаковая амплитудная характеристика, что совершенно очевидно из анализа длины векторов. Однако фазовые характеристики, соответствующие рис. 8.16(a) и (б), совершенно отличны. На рис. 8.17 изображены минимально-фазовая характеристика для полюса и нуля на рис. 8.16 (о) и неминимально-фазовая характеристика для полюса и нуля на рис. 8.16 (б). Ясно, что передаточной функции
.9 4- 2
<?,(*)=—
5+ р
соответствует изменение фазового сдвига в пределах 80°, тогда как для передаточной функции
s— Z
G2(s) =
S+ р
фазовый сдвиг изменяется в пределах 180°. Таким образом, рис. 8.17 иллюстрирует смысл понятия минимальный фазовый сдвиг. При одинаковых амплитудно-частотных характеристиках минимально-фазовой передаточной функции соответствует наименьший возможный фазовый сдвиг, тогда как для неминимально-фазовой передаточной функции фазовый сдвиг всегда больше первого.
|
|
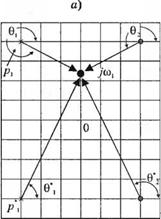
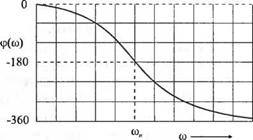
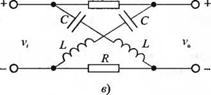
Весьма интересной неминимально-фазовой, схемой является четырёхполюсник, пропускающий все частоты, изображённый на рис. 8.18 (в). Нули его передаточной функции расположены симметрично полюсам относительно мнимой оси, как показано на рис. 8.18 (а). Ещё раз можно убедиться, что |G(/co)| является постоянным и в данном случае он равен единице. Однако фазовая характеристика изменяется от 0° до -360°. Поско-
|
|
Рис. 8.16. Расположения полюса и нуля, соответствующие одинаковым амплитудным и
|
V |
Ч |
|||||||||||||
|
N |
||||||||||||||
|
Неминимальная |
||||||||||||||
|
-N |
фс |
іза |
||||||||||||
|
N |
||||||||||||||
|
/ |
ч |
|||||||||||||
|
Ч |
Ч |
разным фазовым характеристикам Рис. 8.17 180“
Фазовые характеристики для минимально-фазовой и неминимально-фазовой
передаточных функций 9QO
о°
|
|
|
б) |
|
|
|
Рис. 8.18. Четырехполюсник, пропускающий все частоты: (а) расположение полюсов и нулей, (б) частотные характеристики и (в) электрическая схема |
|
|
|
R |
N
льку 02 = 180° — 0j и 0* =180° — 0j, то фазовая характеристика определяется уравнением ф(ю) = -2(01 + 0[ ). Амплитудная и фазовая частотные характеристики данного четырёхполюсника изображены на рис. 8.18 (б).