СОВРЕМЕННЫЕ СИСТЕМЫ УПРАВЛЕНИЯ

Построение корневого годографа

Этап 1: Записать характеристическое уравнение в виде

1 + F(s) = О (7.22)

и, если необходимо, модифицировать его так, чтобы варьируемый параметр К входил в уравнение как множитель:

1 + KP(s) = 0. (7.23)

Этап 2: Представить P(s) в виде дроби, используя полюсы и нули этой функции:

м

FH5+z')

1 + Л:--^------------ =0. (7.24)

Этап 3: Разместить полюсы и нули на s-плоскости, отметив их выбранными услов­ными обозначениями. Обычно представляют интерес траектории корней при изменении параметра К от 0 до со. Из (7.24) мы имеем:

п М

П(*+;>/)+*П (*+**)=а (?-25)

7=1 /=1

При К = 0 корни характеристического уравнения просто совпадают с полюсами P(s), а при К = оо они совпадают с нулями P(s). Следовательно, при изменении К от 0 до со траекто­рии корней характеристического уравнения 1 +KP(s) = 0 начинаются в полюсах P(s) и заканчиваются в нулях /*(.*). У большинства функций Р(.ч), с которыми мы будем иметь

дело, некоторые нули располагаются в бесконечности на 5-плоскости. Это объясняется

тем, что у этих функций P(s) полюсов больше, чем нулей. При 77 полюсах и М нулях, если п>М, п -Мветвей корневого годографа стремятся к п - М нулям, расположенным в беско­нечности.

Этап 4: Выделить отрезки действительной оси, которые принадлежат корневому го­дографу. Участки корневого годографа, совпадающие с действительной осью, всегда лежат слева от нечетного числа полюсов и нулей. Этот факт вытекает из анализа угло­вого критерия (7.17). Все четыре первых этапа построения корневого годографа мы про­иллюстрируем примером.

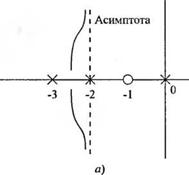
Пример 7.1. Система второго порядка

Одноконтурная система управления имеет следующее характеристическое уравнение (этап 1):

1 + GH (s) = 1 + -* (°’5* = 0. (7.26)

ї(0,25ї + I)

Этап 2: Передаточную функцию C, H(s) перепишем с использованием её полюсов и нулей:

1+ 2Kis+2K0, (7.27)

s(f+4)

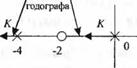
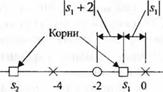
где варьируемый параметр представлен в виде явного множителя 2К. Для построения корне­вого годографа (этап 3) мы сначала поместим на действительную ось полюсы и нуль разо­мкнутой системы, как показано на рис. 7.6 (а). Наконец, заметим, что угловой критерий удов­летворяется на дейсгвительной оси между точками 0 и -4, т. к. аргумент полюсар, в начале ко­ординат равен 180°, а аргументы нуля и полюсар2 в точке. у = -4 равны нулю. Корневой годог­раф начинается в полюсах и заканчивается в нулях, как показано на рис. 7.6 (б), причём направление возрастания параметра К отмечено стрелками. Заметим также, что поскольку ра-

Рис. 7.6. (a) Нуль и полюсы системы второго порядка.

(б) участки корневого годографа и (в) модули каждого вектора при корне s,

зомкнутая система имеет два действительных полюса и один действительный нуль, то второй участок годографа заканчивается в нуле в минус бесконечности. Чтобы найти значение К, со­ответствующее определённому положению корней, воспользуемся амплитудным критерием

. Например, если один из корней, s = = — 1 , то мы имеем:

2А>, + 2|

|s,||s, + 4| І-1Ц-1+ 4|

(7.28)

2|-1+2|

Это значение можно также найти графически, как показано на рисунке 7.6 (в). При К = 3/2 вто­рой корень располагается слева от полюса в точке -4 . Положение этого корня определяется графически: он находится в точке s = - 6 , как показано на рис. 7.6 (е).

Теперь перейдем к следующим этапам построения корневого годографа.

Этап 5: Определить число ветвей корневого годографа, SL. Поскольку корневой го­дограф начинается в полюсах и заканчивается в нулях передаточной функции разомкну­того контура, а число полюсов всегда больше или равно числу нулей, то число отдель­ных ветвей годографа равно числу полюсов. Так, корневой годограф на рис. 7.6 состо­ит из двух ветвей, поскольку система имеет два полюса и один нуль.

Этап 6: Корневой годограф должен быть симметричен относительно действитель­ной оси, т. к. комплексные корни могут появляться только комплексно-сопряжёнными парами.

Этап 7: К нулям, расположенным в бесконечности, корни стремятся вдоль асимптот, проведенных из центра в точке оА под углами ц>А. Если число конечных нулей функции P(s), г., меньше числа её полюсов, пр, то N ветвей корневого годографа должны при К —> со заканчиваться в нулях, расположенных в бесконечности (здесь N = пр - п.). Асимп­тоты корневого годографа образуют /V-лучевую звезду, центр которой находится на дей­ствительной оси. Координата центра определяется выражением:

м

V Df V Г п/ 5^ Pj) Z' )

У полюсов Р(я)~ У нулей P(s) J = l

1=1

Пр-П1

Углы наклона асимптот к действительной оси имеют значения:

Это правило особенно полезно при определении примерного вида корневого годог­рафа. Выражение (7.30) легко может быть получено из рассмотрения точки корневого го­дографа, расположенной на s-плоскости на большом расстоянии от конечных полюсов и нулей. Чистое изменение аргумента в этой точке равно 180°, потому что она принадлежит корневому годографу.

Конечные полюсы и нули функции P(s) находятся на большом расстоянии от этой удалённой точки, поэтому углы ф векторов, проведенных в неё из каждого полюса и нуля, одинаковы и, следовательно, собственный аргумент этой точки равен <р (пр - и,), где пр и п. есть соответственно число конечных полюсов и нулей. Таким образом, мы имеем:

ф(Ир - и:) = 180°.

или, что то же самое,

180°

<р =

Произведя вычисления для всех возможных ветвей корневого годографа, мы получим фор­мулу (7.30).

Центр симметрии прямолинейных асимптот, часто называемый центроидом, нахо­дится по характеристическому уравнению 1 + GH(s) = 0 (уравнение вида 7.24). При боль­ших значениях s определяющую роль играют члены высшего порядка, поэтому характе­ристическое уравнение сводится к виду:

Однако при такой аппроксимации центр симметрии (п — М) асимптот находится в начале координат, s = 0. Лучшей аппроксимацией является представление характеристического уравнения в виде:

где центроид находится в точке аА.

Положение центроида определяется из рассмотрения первых двух членов уравнения (7.24), записанного в виде:

)=•

На основании выражения (6.5) можно записать:

м

Учитывая только два первых члена разложения функции P(s), имеем

К

В свою очередь, уравнение

К

1+-

/ л _ п - М

(s-oA )

с учетом первых двух членов принимает вид:

1 + —------------------------------------------------------------------------- =0.

п-М и—М-1

►У —(n-M)<JAs Приравнивая коэффициенты при s" м~ получим: что эквивалентно выражению (7.29). Например, для системы, изображённой на рис. 7.2, характеристическое уравнение имеет вид:

1+ К = 0. s(s + 2)

Поскольку пр-п, = 2, то следует ожидать, что две ветви корневого годографа будут закан­чиваться в нулях, расположенных в бесконечности. Асимптоты корневого годографа име­ют центр в точке сА =--=-1 2 и составляют с действительной осью углы Ф/l = 90°> <7=0 и Фа - 270°, <7=1. Следовательно, легко можно построить корневой годограф, как это и было продемонстри­ровано на рис 7.3. Ниже мы ещё на одном примере покажем, как можно использовать асим­птоты корневого годографа.

Пример 7.2. Система четвёртого порядка

Одноконтурная система с обратной связью имеет характеристическое уравнение

1 + СЯ(*)=1+ Я*+ 1} - . (7.31)

ф+2)(*+4)2

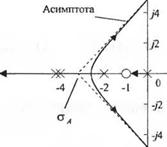
Найдём вид корневого годографа в зависимости от параметра К. Положение на s-плоскости полюсов и нуля показано на рис. 7.7 (а). Участки корневого годографа, принадлежащие дейст­вительной оси, должны быть слева от нечётного числа полюсов и нулей; на рис. 7.7 (а) это по­казано жирными линиями. Центр асимптот находится в точке

(-2)+2И)-(-1)__9 ^ 4-1 3

Поскольку пр - п. = 3, то мы имеем три асимптоты, расположенные под углами

(рА = + 60°, q = 0 , ipA = 180°, <7=1,

ц>А = 300°, q = 2 .

Кроме этого, мы знаем, что ветви корневого годографа должны начинаться в полюсах, поэто­му два корня начнут своё движение из кратного полюса в точке s = - 4 . Располагая асимптота­ми, мы можем изобразить вид корневого годографа, как это показано на рис. 7.7 (б). Точный вид годографа вблизи центроида оА при необходимости можно определить графически.

Участки корневого

годографа

■Ж---

I -4 -2 -1 0

Кратный

полюс

Продолжим рассмотрение этапов построения корневого годографа.

Этап 8: Определить точки, в которых корневой годограф пересекает мнимую ось (если такие точки имеются). Пересечение корневым годографом мнимой оси легко установить с помощью критерия Рауса-Гурвица.

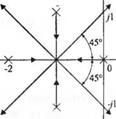
Этап 9: Определить точки отрыва корневого годографа от действительной оси (если такие точки имеются). Точка отрыва корневого годографа от действительно оси — это то место, где сходятся несколько корней, как правило, два. На рис. 7.8 (а) показана точка отрыва для системы второго порядка, а на рис. 7.8 (б) — для частного случая системы четвёртого порядка. Согласно угловому критерию, касательные к корневому годогра­фу в точке отрыва разделены углами, составляющими целую часть от 360°. Так, на рис. 7.8 (а) мы видим, что в точке отрыва угол между двумя ветвями корневого годографа составляет 180°, а на рис. 7.8 (б) четыре ветви разделены углами в 90°.

Точку отрыва на действительной оси можно определить графически или аналитиче­ски. Наиболее простой метод состоит в модификации характеристического уравнения так, чтобы варьируемый параметр К был выделен в одной части от знака равенства. Иначе говоря, характеристическое уравнение записывается в виде:

p(s) = К

Например, для системы с единичной обратной связью, которая в разомкнутом состоянии имеет передаточную функцию

о)

или, иначе:

и—і

да: _ -(Ал)

As ~ С,

Устремляя As к нулю, получим условие

^=0,

ds

которое должно выполняться в точках отрыва. Теперь рассмотрим частный случай, когда

G(s) = К

(з+2)(л+4)

Отсюда:

К = p(s) = -(s+2)(s + 4) = -(s2 +fo+8) Дифференцируя p(s), имеем:

= -(2s+6) = 0,

откуда следует, что точка отрыва находится при s = - 3 . Далее мы рассмотрим более слож­ный пример, с помощью которого проиллюстрируем графический метод определения точ­ки отрыва.

Пример 7.3. Система третьего порядка

На рис. 7.10 изображена система управления, характеристическое уравнение которой имеет вид:

+G(s)H(s)=+ =0.

s(s + 2)(ї+ 3)

W(v)

s + 3

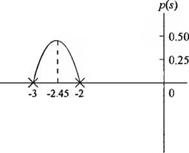
Разность числа полюсов и нулей, пр-п: = 2, поэтому имеются две асимптоты под углами ± 90° с центром в точке аА= — 2. Асимптоты и участки корневого годографа, принадлежащие дейст­вительной оси, показаны на рис. 7.11 (а). Т очка отрыва находится между j=-2hj — 3. Чтобы найти её точное положение, перепишем характеристическое уравнение и выделим параметрі:

ф + 2)(ї + 3) + K(s + 1) = 0,

или

-Ф±2Х£±3) = ^ (?46)

1

Рис. 7.11. Определение (а) асимптот и (б) точки отрыва

Результат вычисления p(s) при различных значениях s между s = -2 и s = -3 отражён в табл. 7-Ій представлен в виде графика на рис. 7.11 (б). Альтернативный способ заключается в дифференцировании выражения (7.46) и приравнивании производной нулю:

d ("-ф+ 2)С?+ ЗЛ _ (д3 + 5s2 + 6s) - (s + l)(3s2 + 10s + 6) _

ds I. s +1 J (s +1)2

ИЛИ

2s3 + 8s2 + 10s + 6 = 0 . (7.47)

Вещественный корень этого уравнения s = - 2.45 определяет максимальное значение p(s). Из этого примера очевидно, насколько эффективным является применение вычислений функции p(s) вблизи ожидаемой точки отрыва для определения её истинного положения.

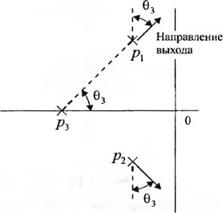
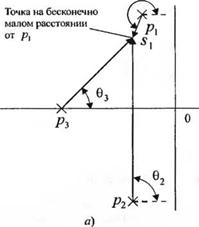
Этап 10: Используя угловой критерий, определить угол выхода корневого годографа из полюса и угол его входа в нуль. Угол выхода корневого годографа из полюса равен разности между суммой аргументов векторов, проведённых в данный полюс из всех остальных полюсов, и суммы аргументов векторов, проведённых в данный полюс из всех нулей, плюс угловой критерий ±(2q + 1)180°. То же самое справедливо для угла входа корневого годографа в нуль. Углы выхода и входа представляют интерес в случае комплексных полюсов и нулей, т. к. эта информация позволяет уточнить вид корневого годографа. Например, рассмотрим систему третьего порядка, передаточная функция ко­торой в разомкнутом состоянии имеет вид:

F(s) = G(s)H(s) =------------ ^(7.48)

(5 + /?з )Сг +2^(0„5+(0-)

На рис. 7.12 (а) показано расположение трёх полюсов и отмечены аргументы векторов, проведенных в комплексный полюс рх. Сумма аргументов всех векторов для тонкие,, нахо­дящейся на бесконечно малом расстоянии от рх, должна удовлетворять угловому крите­рию. Таким образом, учитывая, что 02 = 90°, мы имеем:

б)

Рис. 7.12. Определение угла выхода: (а) проверка углового критерия в точке, находящейся на бесконечно малом расстоянии от pi, и

(б) действительное направление выхода из полюса р,

а это значит, что угол выхода из полюса рх равен 0, = 90° - 03, как показано нарис. 7.12 (б). Угол выхода из полюса р2 отличается от 0, лишь знаком (минус), поскольку рх и р2 являются комплексно-сопряжёнными. Дру­гой пример определения угла выхода приведён на рис. 7.13. В данном случае угол выхода находится из выражения

02 - (0, + 03 + 90° ) = 180°.

Поскольку (02 - 03)=Y, то угол выхода 0, = 90° + у.

Заключительные два этапа процедуры постро­ения корневого годографа связаны с определением положения корней sx и значения параметра К„ со­ответствующего этому положению.

Этап 11: Определить положение корней sx, х= 1, 2,..., пр, которые удовлетворяют угловому Рис. критерию. Угловой критерий (см. выражение 7.17) имеет вид:

arg F(s) = 180° ± q360°, q = 1, 2, ...

Этап 12: Используя амплитудный критерий (7.16), определить значение параметра К„ соответствующее корню sx. Для корня sx амплитудный критерий имеет вид:

П>+Л/1

к =

nij+z-

/=1

Теперь полезно собрать воедино все 12 этапов, связанных с построением корневого годографа, что и сделано в табл. 7.2, а затем проиллюстрировать их завершающим приме­ром.

Таблица 7.2. 12 этапов построения корневого годографа

Этап

1. Записать характеристическое уравнение так, чтобы варьируемый параметр К входил в него в виде множителя.

2. Записать P(s), используя пр полюсов и п: нулей этой функции.

3. Выбрав подходящие символы, отметить на. s-плоскости положения полюсов и нулей ра­зомкнутой системы.

4. Отметить участки действительной оси, при­надлежащие корневому годографу.

5. Определить число отдельных ветвей корне­вого годографа, SL.

6. Траектории корней симметричны относите­льно действительной оси.

7. К нулям, расположенным в бесконечности, корни стремятся вдоль асимптот с центром в точке Оу). образующих с действительной ОСЬЮ углы фл-

8. С помощью критерия Рауса-Гурвица опреде­лить точки, в которых корневой годограф пересекает мнимую ось (если такие точки имеются).

9. Определить точки отрыва корневого годог­рафа от действительной оси (если такие точки имеются).

10. С помощью углового критерия определить углы выхода корневого годографа из комп­лексных полюсов и углы входа в комплекс­ные нули.

11. Определить положение корней, при кото­ром выполняется угловой критерий.

12. Определить параметр Ксоответствующий каждому корню sx.

Уравнение или правило

1 + KP(s) = 0.

П> + г<)

1+ К -------------- = 0.

/=і

X — полюсы, О — нули, □ или Л — корни характеристического уравнения замкнутой системы. Траектории корней начинаются в полюсах и заканчиваются в нулях.

Эти участки расположены слева от нечетного числа полюсов и нулей.

SL = Пр, если Пр > п2 пр — число конечных полюсов. п2 — число конечных нулей.

Z(-P/)-Z(-z,)

°А = ■

Пр-П.

Фл = • 180°. q = 0,1.2„.„(Пр - п.- 1).

Пр - п.

См. раздел 6.2

а) Положить К = p(s):

б) Получить уравнение dp(s)/ds = 0;

в) Найти корни (б) или графически опреде­лить положение максимума p(s).

arg Р(ї)=180° ± q360° при s = р, или z, . arg P(s) = 180° ± <y360° при корне sx.

Пк*+л)і

Kx =~-------------

Пк*+2.)і

Пример 7.4. Система четвертого порядка

1. Построим корневой годограф для системы, имеющей характеристическое уравнение

К

= 0.

s4 + 12s3 + 64s2 + 128s

где К — варьируемый параметр (К > 0).

2. Определив полюсы передаточной функции, запишем:

К

1 +

s(s + 4)(s + 4 + /4 )(s + 4-/4)

Параметр К будем менять от 0 до вд. Заметим также, что система не имеет конечных нулей.

3. Отметим на s-плоскости положение полюсов, как показано на рис. 7.14 (я).

4. Участок корневого годографа, принадлежащий действительной оси. расположен между s = 0 и s = - 4.

5. Поскольку мы имеем 4 полюса (пр = 4), то корневой годограф содержит 4 ветви.

6. Траектории корней симметричны относительно действительной оси.

7. Асимптоты расположены под углами

Ф/)=^^-180°. 0.1.2.3:

4

(рА = + 45°, 135°, 225°, 315°.

Центр асимптот находится в точке

-4-4-4 о, =--- = -3.

Эти асимптоты изображены пунктирными линиями на рис. 7.14 (а).

8. Перепишем характеристическое уравнение в виде:

s(s + 4 )(s2 + 8s + 32)+ К = s4 + 12s3 + 64s2 + 128s + A = 0.

Рис. 7.14. Корневой годограф для примера 7.4:

(а) положение полюсов и (б) асимптоты

Составим таблицу Рауса:

, 12-64-128 53,33 128-ПК

где b = -------------- = 53,33 и с, =--------------------- .

12 1 53,33

Следовательно, система находится на границе устойчивости при К - 568,89. исходя из чего не­трудно найти корни вспомогательного уравнения:

53,33s2 + 568,89 = 53,33(s2 + 10,67) = 53,33(s + A266)(s -./3,266). (7.51)

Точки, в которых корневой годограф пересекает мнимую ось, показаны на рис. 7.14 (а).

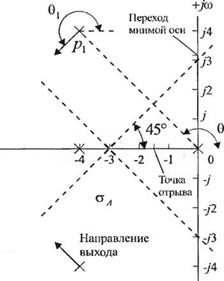
9. Точка отрыва находится путём вычисления выражения

К = p(s) = - s(s + 4)(s + 4 + /4)(s + 4 —j‘4) при значениях s между s = -4hs = 0. Можно ожидать, что эта точка лежит где-то между s = — 3 и s = - 1, поэтому будем искать максимум p(s) в этом диапазоне. Для некоторых значений s вы­числения сведены в табл. 7.3, откуда видно, что максимум p(s) имеет место приблизительно при s = — 1.5. Более точной оценки положения точки отрыва обычно не требуется. Точка отры­ва указана на рис. 7.14 (о).

Таблица 7.3

P(s) 0 51 68.5 80 85 75 0

s______ -4.0 -3.0______ =2,5______ -2.0 -1.5 -1.0_____ 0

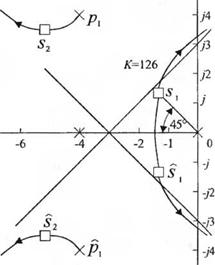
10. Угол выхода из комплексного полюсар, можно определить с помощью углового критерия:

0, + 90° + 90° + 03 = 180°,

где 03 — угол, образованный вектором, проведённым в полюс р, из полюсар3 . Каждый из уг­лов, образованных векторами, проведёнными в р, из полюсов при s = -4ms = -4 - /4, равен 90°. Поскольку 03 = 135°, то мы имеем:

0! =- 135° = + 225°,

как показано на рис. 7.14 (о).

11. Определяем положение корней, удовлетворяющее угловому критерию, как показано на рис. 7.14 (б).

12. Находим значение К при s = sx.

Информации, полученной за 12 перечисленных этапов, достаточно для того, чтобы полностью построить корневой годограф. Для рассматриваемой в примере системы корневой годограф изображён на рис. 7.14 (б). Если комплексным корням, расположенным вблизи начала коорди­нат, соответствует коэффициент затухания Q = 0.707, то по рис. 7.14 (б) можно графически определить значение параметра К. Для этого достаточно вычислить модули векторов, прове­денных в точку s| из полюсов разомкнутой системы. В результате мы получим:

К =|s1||sl + 4||sl-fl||s1-p|=(l,9)(2,9)(3,8)(6.0)= 126. (7.52)

Другая пара комплексных корней при К= 126 занимает положение s2 и s2. Влияние этих кор­ней на переходную характеристику будет незначительным по сравнению с корнями s, и sj. В этом можно убедиться, оценив степень затухания реакции, обусловленной каждой парой кор­ней. Затухание за счёт корней s, и s, определяется экспонентой

а за счёт корней s2 и s2 — экспонентой

е-С2“П2' =е-°2» >

где о2 почти в 5 раз больше, чем ст, . Поэтому составляющая реакции системы, обусловленная корнем s2, будет затухать намного быстрее, чем составляющая, обусловленная корнем s,. В ре­зультате реакцию системы на единичное ступенчатое воздействие можно представить в виде:

y(t) = + СЄ~С'' sinCcOjf + B, )+С2е_°2' sin((O2^ + 02)SBl+C,1e'‘O‘' sinCa»! / - I - 0! ) (7.53)

Комплексно-сопряжённые корни, которые среди всех корней ближе всего расположены к на­чалу координат s-плоскости, называются доминирующими корнями, поскольку именно они в основном определяют вид переходной характеристики системы. В системе третьего порядка при наличии двух комплексно-сопряжённых корней их можно считать доминирующими, если значение третьего (действительного) корня не менее чем в 5 раз превышает действительную часть комплексно-сопряжённых корней.

Преобладание второго члена в выражении (7.53) зависит также от относительной величины коэффициентов с| и с2. Эти коэффициенты, которые определяются как вычеты в комплексных полюсах, в свою очередь зависят от положения нулей на s-плоскости. Поэтому понятие доми­нирующих корней, хотя и является полезным для оценки реакции системы, но должно исполь­зоваться с осторожностью и с пониманием указанных выше факторов.

Точку отрыва и другие характерные точки корневого годографа легко можно опреде­лить с помошью MATLAB. Например, в примере 7.2 точка отрыва появляется при К = 1,925, когда два действительных корня сходятся при s = - 2,6. Если К = 200, то два корня находятся на мнимой оси при s = ± J4.82.

В примере 7.4 (опять-таки с помощью MATLAB) можно найти, что точка отрыва от действительной оси, s = - 1,57, появляется при К= 84, а при К= 600 два корня, s = ±/5,33, находятся на мнимой оси.