СОВРЕМЕННЫЕ СИСТЕМЫ УПРАВЛЕНИЯ

Определение характеристик систем управления с помощью MATLAB

В этом разделе мы с помощью MATLAB на двух примерах проиллюстрируем преимущест­ва введения обратной связи в системы управления. В первом примере мы покажем, как за счет обратной связи можно добиться компенсации возмущений в системе управления ско­ростью двигателя. Эта система была рассмотрена в разделе 4.3. Во втором примере мы по­кажем, как в системе управления бурильной машиной (см. разд. 4.7) обратная связь позво­ляет уменьшить чувствительность к изменению параметров объекта, скорректировать вид переходной характеристики и уменьшить установившуюся ошибку.

Пример 4.2. Система управления скоростью

Структурная схема разомкнутой системы управления скоростью вращения двигателя при на­личии возмущающего момента TJs) приведена на рис. 4.11. Параметры этой системы приведе­ны в табл. 4.2. Система имеет 2 входа: VJs) и TJs). В соответствии с принципом суперпози­ции, применимом к линейным системам, мы можем рассматривать каждый вход отдельно от другого. Чтобы исследовать влияние возмущений на систему, мы положим VJs) = 0 и будем рассматривать только вход TJs). И наоборот, чтобы исследовать реакцию системы на эталон­ный входной сигнал, мы положим TJs) = 0 и будем рассматривать вход VJs).

Таблица 4.2. Параметры системы управления скоростью

электродвигателя

Структурная схема замкнутой системы с тахогенератором в пегш обратной связи изображена на рис. 4.13. Параметры Ка и К, также приведены в табл. 4.2.

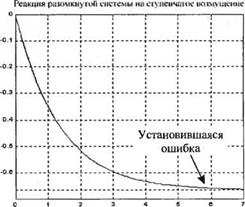
Если система хорошо компенсирует возмущения, то мы можем ожидать, что TJs) слабо будет влиять на скорость co(s). Рассмотрим сначала разомкнутую систему на рис. 4.11. Мы можем с помощью MATLAB определить передаточную функцию от TJs) к co(s) и вычислить реакцию выходной переменной на единичное ступенчатое возмущение, т. е. TJs) = Us. Эта реакция приведена на рис. 4.27(a). Вычисления произведены с помощью скрипта opentach. m, приве­денного на рис. 4.27(б).

Разомкнутая система имеет передаточную функцию

где sys_0 в срипте MATLAB соответствует передаточной функции разомкнутой системы. По­скольку желаемое значение со(0 равно нулю [напомним, что VJs) = 0], то установившаяся

Рис. 4.27

Анализ

разомкнутой

системы

управления

скоростью.

(а) Реакция на возмущение и

(б) скрипт MATLAB

б) opentach. m

% Система управления скоростью двигателя (пример)

%

Ra=1; Km=10; J=2; b=0.5; Kb=0.1; num1=[1]; den1=[J, b]; sys1=tf(num1,den1); num2=[Krn*Kb/Ra]; den2=[1]; sys2=tf(num2,den2); sys_o=feedback(sys1 ,sys2);

%

sys_o=-sys_o; <------------

%

[yO, T]=step(sys_o);-<------

plot(T, yO)

Ше(‘Реакция разомкнутой системы на ступенчатое возмущение’) хІаЬеІ(‘Время (с)’), ylabel(‘omega_0’),grid

%

Установившаяся ошибка : значение выхода уО

ошибка просто будет совпадать с конечным значением со(/), которое мы обозначим через со0(0, чтобы подчеркнуть, что речь идет о разомкнутой системе. Установившаяся ошибка, показан­ная на графике на рис. 4.27(a), приблизительно равна значению скорости спустя время t = 1 с. Это значение можно рассматривать как последнее значение вектора выхода у0, вычисленное в процессе построения графика на рис. 4.27(e). Приблизительное значение со0(оо) равно:

со0(оо) к со0(7) = - 0,66 рад/с.

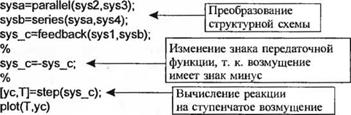
Г рафик показывает, что система действительно достигает установившегося состояния. Аналогичным образом мы начнем анализ замкнутой системы с определения передаточной функции от TJs) к co(s) и вычисления реакции со(/) на единичное ступенчатое возмущение. Эта реакция и соответствующая программа closedtach. m приведены на рис. 4.28. Передаточная функция замкнутой системы по отношеншо к возмущению равна

со(г) _ 1

- sys_c

Td(s) 2s + 541,5

Как и ранее, установившаяся ошибка равна конечному значению со(<), которое мы обозначим через cot.(f), чтобы подчеркнуть, что речь идет о замкнутой системе. Эта ошибка отмечена на графике на рис. 4.28(a). Ее можно рассматривать как последнее значение вектора выхода ус.

Рис. 4.28

Анализ замкнутой системы управления скоростью.

(а) Реакция на возмущение и

(б) скрипт MATLAB

б) closedtach. m

% Система управления скоростью двигателя (пример) %

Ra=1; Km=10; J=2; b=0.5; Kb=0.1; Ka=54; Kt=1; num1=[1]; den1=[J, b]; sys1=tf(num1,den1); num2=[Ka*Kt]; den2=[1]; sys2=tf(num2,den2); num3=[Kb]; den3=[1]; sys3=tf(num3,den3); num4=[Km/Ra]; den4=[1]; sys4=tf(num4,den4);

1 Установившаяся ошибка = последнее

значение выхода ус

вычисленное в процессе построения графика нарис. 4.28(a). Установившееся значение со при­близительно равно

соДоо) и сос(0,02) = - 0,002 рад/с.

Сравнение установившегося значения скорости в замкнутой и разомкнутой системах при еди­ничном ступенчатом возмущении дает результат:

С00(о°)

Отсюда видно, что введение отрицательной обратной связи позволило значительно умень­шить влияние возмущения на выходную переменную. Это демонстрирует свойство замкнутых систем компенсировать возмущения.

Рис. 4.29

Реакция системы на ступенчатый входной сигнал при {а) К = 100 и (б) при К = 20.

(в) Скрипт MATLAB

Є)

englishl.m

% Переходные характеристики при К=20 и К=100 % numg=[1]; deng=[1 1 0]; sysg=tf(numg, deng); К1=100; К2=20;

num1=[11 К1]; num2=[11 К2]; den=[0 1];

sys1=tf(num1,den); sys2=tf(num2,den);

%

sysa=series(sys1 ,sysg); sysb=series(sys2,sysg); sysc=feedback(sysa,[1]); sysd=feedback(sysb,[1]);

%

t=[0:0.01:2.0]; <-------------------------

Задание интервала времени

[у1 ,t]=step(sysc, t); [y2,t]=step(sysd, t); subplot(211),plot(t, y1), МІе(‘Переходная характеристика при К=100') хІаЬеІ(‘Время (с)’), ylabel(‘y(t)’),grid subplot(212), plot(t, y2), МІе(‘Переходная характеристика при К=20’) хІаЬеІ(‘Время (с)'), ylabel(‘y(t)’),grid <

Построение графиков с разметкой осей х и у

ристики с помощью коэффициента К. На основании полученных результатов по-видимому предпочтительнее выбрать значение К = 20. Однако нужно принять к рассмотрению и некото­рые другие соображения, прежде чем окончательно завершить процедуру синтеза.

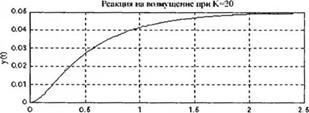
Учитывая сказанное выше, полезно рассмотреть реакцию системы на единичное ступенчатое возмущение, как показано на рис. 4.30. Мы видим, что увеличение К приводит к уменьшению установившегося значения y(t). Это значение равно 0,05 и 0,01 при К= 20 и 100, соответствен­но. Показатели качества (установившаяся ошибка еуст. максимальное относительное перерегу­лирование сттах и время установления Ts при критерии 2%) сведены в табл. 4.3. Установившие­ся значения >’(/) можно также предсказать с помощью теоремы о конечном значении:

1

lim^f) = lim. у

/-КО А-Х)

s(j+12)+ К

Если целью синтеза является только компенсация возмущения, то предпочтительнее выбрать К= 100.

Рис. 4.30

Реакция системы на ступенчатое возмущение при

(а) К = 100 и

(б) при К = 20.

(в) Скрипт MATLAB

б)

english2.m

% Реакция на возмущение D(s)=1/s при К=20 и К=100 %

numg=[1]; deng=[1 1 0]; sy sg=tf(numg, deng);

K1=100; K2=20;

num1=[11 К1]. num2=[11 K2J; den=[0 1]; sysl =tf(num1 ,den); sys2=tf(num2,den);

%

sysa=feedback(sysg, sys1); sysa=minreal(sysa); sysb=feedback(sysg, sys2); sysb=minreal(sysb);

%

t=[0:0.01:2.5];

[y1 ,t]=step(sysa, t); [y2,t]=step(sysb. t);

subplot(211), plot(t, y1), М1е(‘Реакция на возмущение при К=100') хІаЬеІ(‘Время (с)’), ylabel(‘y(t)’),grid

subplot(212), plot(t, y2), ШІе(‘Реакция на возмущение при К=20’)

хІаЬеІ(‘Время (с)’), ylabel(‘y(t)’),grid < Построение графиков

с разметкой осей ли у

Мы уже встречались с распространенной ситуацией поиска компромисса при синтезе системы управления. В данном примере увеличение К приводит к лучшей компенсации возмущения; с другой стороны, при уменьшении К улучшается качество системы (меньше перерегулирова­ние). Окончательное решение по поводу выбора К остается за проектировщиком.

Хотя MATLAB может оказать существенную помощь при синтезе системы управления, он ни в коем случае не может заменить интуицию инженера и его способность принимать решения.

В завершение анализа необходимо оценить чувствительность системы к изменению парамет­ров объекта. Эта чувствительность определяется выражением (4.62):

sr _ s(s+ 1) а j(j+12)+K'

Мы можем вычислить значения Sj;(s) для различных значений j и изобразить чувствитель­ность в виде графика. На низких частотах приближенно можно считать

с г s К

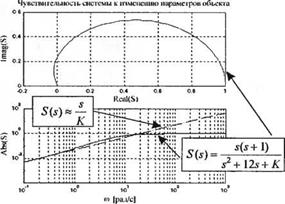
Увеличение коэффициента К приводит к уменьшению чувствительности системы. Графиче­ское изображение зависимости чувствительности от j =j(a при К = 20 приведено на рис. 4.31. Рис. 4.31

(а) Чувствительность системы к изменению параметров объекта (s =/»).

(б) Скрипт MATLAB

«)

б) english3.m

% Г рафик чувствительности системы

%

К=20; num=[1 1 0]; den=[1 12 К]; w=logspace(-1,3,200); s=w*i; Ч— n=s. A2+s; d=s. A2+12*s+K; S=n./d; n2=s; d2=K; S2=n2./d2;

% --------------------------------------------------------

Задание вектора j = ym для оценки чувствительности

Чувствительность

Оценка чувствительности по приближенной формуле