СОВРЕМЕННЫЕ СИСТЕМЫ УПРАВЛЕНИЯ
Модели систем в переменных состояния в виде сигнального графа
Выше мы рассмотрели случай, когда состояние системы и ее динамика описываются рядом дифференциальных уравнений первого порядка. В качестве альтернативы может быть использовано уравнение состояния вида (3.16). В любом случае будет полезно получить модель системы в виде сигнального графа, узлы которого соответствовали бы переменным состояния, а затем установить связь между таким графом и уже известным нам представлением системы в виде передаточной функции.
Как было показано ранее, система может быть полностью описана передаточной функцией G(s), связывающей ее входную и выходную переменные. Например, если нас интересует связь между входным и выходным напряжением в схеме на рис 3.4, то мы можем получить передаточную функцию
V0(s)
G(s) =
U(s)
Передаточная функция RLC-цепи на рис. 3.4 имеет вид
G(s) = 777T=-T-^-------------- • (3-28)
U(s) S" +P-S + у
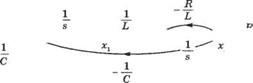
где а, р и у являются функциями параметров цепи R, LuC. Значения а, Р и у можно определить по сигнальному графу, отображающему дифференциальные уравнения, описывающие электрическую цепь. Для нашего случая (см. уравнения 3.8 и 3.9) мы имеем:
*1 +^W(/)’ (3-29)
х2 --^*2. (3.30)
v0 = Rx2. (3.31)
|
Рис. 3.5. Сигнальный граф для RLC-цепи |
|
|
|
Щз) о *-------------- Q——----------- О »- Cf—~—ЧЭ О ч, |
Граф, отражающий эту систему уравнений, изображен на рис. 3.5, где 1 Is есть символ интегрирования. По формуле Мейсона мы получим передаточную функцию:
F0(s) R/LCs2 R/LC
(3.32)
U(s) 1 + R/Ls+ VLCs2 s2 +(R/L)s+l/LC
К сожалению, многие электрические цепи, электромеханические системы и другие системы управления не так просты, как схема на рис. 3.4, и часто очень трудно получить дифференциальные уравнения первого порядка, описывающие динамику системы. Поэтому бывает проще получить передаточную функцию системы (хотя бы методами, изложенными в гл. 2) и затем на ее основании построить модель в переменных состояния.
Модель системы в виде графа с переменными состояния в узлах легко получить по передаточной функции. Но, как мы заметили в разд. 3.3, возможны несколько комбинаций переменных состояния и, следовательно, можно изобразить несколько различных сигнальных графов. В общем случае передаточную функцию можно представить в виде
C(s) = W = ^+b^ +-+У+ (3.33)
U(s)
т - л +...+ S + Oq
где n>m и все коэффициенты а и b есть вещественные числа. Умножив числитель и знаменатель на s~n, мы получим:
-(и-m) . („_„,+!) , -(,,-1) ,
G(s) = ----------- —t±S________ +■■•+V + b0s _
1 + an_^s 1 +...+ ^5 4 + o0s "
|
Ела |
Мы уже знакомы с формулой Мейсона, поэтому легко можем увидеть в знаменателе коэффициенты передачи контуров с обратной связью, а в числителе — коэффициенты передачи прямых путей. Напомним формулу Мейсона, приведенную в разд. 2.7:
к
G(5) = ^=^-T----------------- • (3.35)
U(s) А
Если все контуры с обратной связью являются касающимися, а все прямые пути в свою очередь касаются этих контуров, то выражение (3.35) сводится к следующему:
Tpk
к _ Сумма коэффициентов передачи прямых путей
)----------------------------------- — . (j. jOJ
А 1-Сумма коэффициентов передачи контуров
1 - 2-, L4
9=1
Передаточную функцию можно представить различными графами. Представляют интерес два частных случая таких конфигураций, основанных на формуле Мейсона, и мы рассмотрим их более подробно. В следующем разделе мы приведем еще две дополнительных конфигурации графов.
Чтобы проиллюстрировать получение сигнального графа в терминах переменных состояния, рассмотрим сначала передаточную функцию четвертого порядка:
y(s) Z>0 V4
() = 777^Л = 1------------ Г~—’----------------- = 7 ------------------- =2------- =5--------------- Т - (337)
U(s) s + a3s +a2s~+als+a0 + a2s + a3s + aAs
Прежде всего мы заметим, что система имеет четвертый порядок и поэтому нам потребуются четыре переменных состояния (х1; х2, х3, х4). Имея в виду формулу Мейсона, напомним, что знаменатель можно рассматривать как 1 минус сумма коэффициентов передачи контуров, а числитель передаточной функции есть коэффициент передачи прямого пути графа. Сигнальный граф должен содержать минимальное число интеграторов, равное порядку системы. Следовательно, для графического представления данной системы нам потребуются четыре интегратора. Соответствующие узлы и интеграторы сигнального графа отображены на рис. 3.6. Наиболее простая конфигурация из этих элементов, соответствующая передаточной функции, представлена нарис. 3.7. Анализируя этот рисунок, мы можем заметить, что все контуры являются касающимися и, следовательно, передаточная функция имеет вид (3.37). Читатель легко может убедиться, что коэффициент передачи прямого пути действительно равен bg/s, а знаменатель равен единице минус сумма коэффициентов передачи всех контуров.
1 1 1 1
им Т Т Т Т у(*>
о о—*—о о—*—о о—-—о о—-—о о
|
Рис. 3.6. Узлы и интеграторы графа для системы четвертого порядка
'«о |
Рис. 3.7. Граф состояния для G(s), соответствующей выражению (3.37)
Теперь рассмотрим передаточную функцию четвертого порядка, в которой числитель является полиномом переменной S, т. е.
п, Ъз-5,3 + b2s2 + V+ *о b3s~1 + b2s~2 + fe, s“3 + V-4 ,04
G(s) 4 3 ■> -1 -3 _4 ■ (3-38)
s + a3s + a2s +axs+a0 + a2s ~ + + a0s
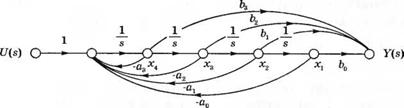
Слагаемые в числителе представляют собой коэффициенты передачи прямых путей в формуле Мейсона. Прямые пути касаются всех контуров, поэтому сигнальный граф выглядит так, как представлено на рис. 3.8. Прямые пути имеют коэффициенты передачи b3/s, b2/s2, b/s* и b0/s4, что соответствует числителю передаточной функции. Еще раз напомним, что в числителе формулы Мейсона всегда содержатся члены числителя передаточной функции, т. е. сумма прямых путей от входа системы к ее выходу. Общий вид графа, представляющего передаточную функцию (3.3 8) на рис. 3.8, включает в себя /? контуров с коэффициентами ап и т прямых путей с коэффициентами передачи Ът. Такое изображение сигнального графа называется представлением в форме фазовой переменной.
|
Рис. 3.8. Граф состояния для G{s) вида (3.38) в форме фазовой переменной |
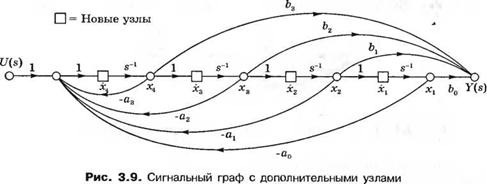
Переменные состояния на рис. 3.8 — это выходы каждого из элементов, накапливающих энергию, т. е. выходы интеграторов. Чтобы получить систему дифференциальных уравнений первого порядка, соответствующую графу на рис. 3.8, мы введем в граф дополнительные узлы, непосредственно предшествующие каждому интегратору. В этом случае каждый такой узел будет соответствовать производной выходной переменной интегратора. Сигнальный граф с дополнительными узлами изображен на рис. 3.9. По этому графу мы теперь можем записать следующую систему дифференциальных уравнений первого порядка, характеризующих состояние модели:
Xj =х2, х2=х3, х3 =х4,
х4 = - а0х1 -ахх2 - а2х3 - а3хл + и, (3.39)
гдехх, х2,... ,хп есть фазовые переменные.
|
|

Выход определяется уравнением
|
(3.40) (3-41) (3.42) |
y(t) = b0xt + bxx2 + Ъ2х3 + Ъ3хл. Те же уравнения в матричной форме имеют вид:
х = Ах + В и,
|
и(0 |
или
|
V |
' 0 |
1 |
0 |
0 |
*1 |
0 |
||||
|
d |
х2 |
0 |
0 |
1 |
0 |
х2 |
0 |
|||
|
--- |
— |
+ |
||||||||
|
dt |
*3 |
0 |
0 |
0 |
1 |
*3 |
0 |
|||
|
_х4_ |
—а0 |
~а1 |
-а2 |
-«з |
Х4 |
1 |
3<О = Сх=[Ь0 і», Ъ2 £>3]
|
(3.43) |
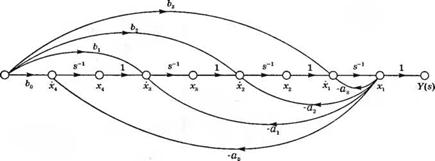
Структура графа, изображенная на рис. 3.8, не является единственно возможным представлением выражения (3.38); другая конфигурация графа, соответствующая той же передаточной функции, изображена на рис. 3.10. В этом случае коэффициенты передачи прямых путей образуются за счет заведения сигнала U(s) на вход каждого из интеграторов. Такую модель мы будем называть структурой с многомерным входом.
Для графа на рис. 3.10 выходной сигналy(t) равен первой переменной состояния х^/). Коэффициенты передачи прямых путей равны b0/s4, fo]/s3, b2/s2, b3/s и все эти пути касаются контуров. Поэтому передаточная функция действительно соответствует выражению (3.38).
По графу, изображенному на рис. 3.10. можно записать следующую систему дифференциальных уравнений первого порядка:
|
= - а^хх + х3 + Ъ2 и, — — £/qX| + Z? Q 11. |
|
(3.44) |
*і = _ язхі +х2 + Ь3 и, х3 = - аххх + х4 + Ъхи,
|
(3.45) |
Те же уравнения, но в матричной форме:
|
-°з |
1 |
0 |
о' |
V |
||
|
dx |
-а2 |
0 |
1 |
0 |
ь2 |
|
|
--- = |
X + |
|||||
|
dt |
~а |
0 |
0 |
1 |
ъ |
|
|
Га о |
0 |
0 |
0 |
Л. |
|
i/(0- |
Хотя графы в виде структуры с многомерным входом и в форме фазовой переменной соответствуют одной и той же передаточной функции, но переменные состояния в них не равны друг другу. Это объясняется тем, что графы имеют разную структуру. Заметим также, что начальные условия в системе можно представить в виде начальных условий для интеграторов, Х](0), х2(0), ... , х„(0). Ниже мы рассмотрим систему управления и получим для нее уравнения состояния, воспользовавшись двумя разными конфигурациями модели.
|
Рис. 3.10. Альтернативный вид графа, соответствующего передаточной функции (3.38) |
|
Пример 3.1. Две модели в переменных состояния ад |
|
Рис. 3.11 Одноконтурная система управления |
|
2(s + l)(s + 3) |
|
G(s) = |
|
Y(s) |
|
s(s + 2)(s + 4) |
|
На рис. 3.11 изображена одноконтурная система управления, которая в замкнутом состоянии имеет передаточную функцию |
|
т. R(s) |
|
2s + 8s + 6 s3 + 8s2 + 16j + 6 |
|
Ш = |
|
Умножая числитель и знаменатель на s' , получим: |
|
2s~' + 8s~2 + 6s~3 R(s) 1+ 8s~' + 16s“2 + 6s“3 |
|
T(s) = ^ = |
|
(3.46) |
|
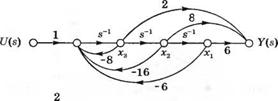
Первая модель в виде графа в форме фазовой переменной изображена на рис. 3.12. В этой модели выходной сигнал образуется как линейная комбинация переменных состояния. Для данного графа уравнение состояния имеет вид: |
|
' 0 |
1 |
0' |
'0' |
||
|
X = |
0 |
0 |
1 |
х + |
0 |
|
-6 |
-16 |
-8 |
1 |
|
«(О, |
|
(3.47) |
|
а уравнение выхода |
|
JK0 = [6 8 2] |
|
(3.48) |
|
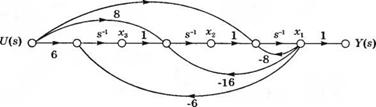
Вторая модель имеет вид графа со структурой с многомерным входом (рис. 3.13). Для нее уравнение состояния имеет вид: |
|
' -8 |
1 |
0‘ |
2 |
|
|
-16 |
0 |
1 |
х + |
8 |
|
-6 |
0 |
0 |
6 |
|
u(t |
|
(3.49) |
|
а выход y{t) = xx(t). |
|
Рис. 3.12 Граф со структурой в форме фазовой переменной |
|
|
|
|
|
Рис. 3.13 Граф в виде структуры с многомерным входом |
Заметим, что оба сигнальных графа, соответствующих передаточной функции Цл), строятся достаточно просто, без разложения числителя и знаменателя на множители. Это позволяет избежать трудоемких вычислений, а по структуре графа легко можно записать уравнение состояния. Каждый из двух сигнальных графов является основой для компьютерного моделирования передаточной функции. Поскольку система имеет третий порядок, то для ее моделирования необходимы три интегратора. Следует, однако, еще раз подчеркнуть, что переменные состояния в модели на рис. 3.12 не идентичны соответствующим переменным в модели на рис. 3.13. В то же время одна комбинация переменных состояния связана с другой соответствующим линейным преобразованием. Используя соотношение z = Мх, мы можем преобразовать вектор х в вектор z с помощью матрицы М. В заключение отметим, что передаточная функция вида (3.33) описывает линейную систему с постоянными коэффициентами, имеющую один вход и один выход, связанные дифференциальным уравнением п-го порядка
d”y d"-ly. . dmu. dm~xu. /ч,„e„
н яи-і і—•■■■-+ аоуО) —------------------------ t - bm_| — +...+ b0u(t).----- (3.50)
dt” dt”-1 dtm dtm-x
В этом разделе на примере сигнальных графов было показано, как можно перейти от одного дифференциального уравнения и-го порядка к системе из п дифференциальных уравнений первого порядка и тем самым — к уравнению состояния.