СОВРЕМЕННЫЕ СИСТЕМЫ УПРАВЛЕНИЯ
Альтернативные модели в виде сигнальных графов
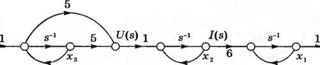
Очень часто при проектировании систем управления специалисту приходится иметь дело со структурной схемой, в которой каждый блок соответствует реальному устройству, а все переменные суть физические величины. Примером может служить разомкнутая система управления скоростью вращения двигателя постоянного тока, изображенная на рис. 3.14. В качестве переменных состояния желательно выбрать реальные физические переменные. Поэтому мы будем использовать следующие переменные: х, = y(t), скорость вращения (она же — выходная переменная); х2 = /(/), ток возбуждения; и хъ = u(t), напряжение возбуждения. Сигнальный граф, содержащий эти физические переменные, изображен на рис. 3.15. Такая модель полезна, в частности, если физические переменные состояния могут быть измерены. Заметим, что на графе каждый блок структурной схемы представлен отдельно. Например, регулятор имеет передаточную функцию
R(s) s+5 l+5s—1
и на графе она представлена фрагментом между R(s) и U{s).
|
Регулятор Двигатель и нагрузка
Рис. 3.14. Структурная схема разомкнутой системы управления скоростью электродвигателя |
#(s) о
|
|
|
О V(S) |
-5 -2 -3
Рис. 3.15. Сигнальный граф с физическими переменными состояния Уравнение состояния записывается непосредственно по графу на рис. 3.15:
|
-3 |
6 |
0 " |
O' |
|
|
0 |
-2 |
-20 |
х + |
5 |
|
0 |
0 |
-5 |
1 |
|
X - |
|
т |
|
(3.51) |
а выходная переменная
у = [1 0 0] х.
Второй способ получения сигнального графа основан на разложении передаточной функции на элементарные составляющие. Передаточная функция, связывающая вход и выход структурной схемы на рис. 3.14, имеет вид:
(3.52)
|
Y(s) R(s) |
|
ф) |
30(5+1)
= Г(5) =
(s+ 5)(s+2)(s+3) (s-sl )(s-s2 )'
а переходная функция имеет три составляющие, определяемые полюсами s,, s2 и s3. Разложение передаточной функции на элементарные дроби дает:
|
А9 |
|
(3.53) |
|
s+ 5 s + 2 5 + 3 |
|
П£)=тад= *' ад |
|
т |
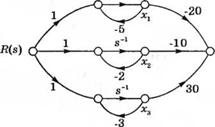
Используя прием, описанный в гл. 2, мы находим, что кх = -20, к2 = -10 и /с3 = 30. Сигнальный граф, соответствующий выражению (3.53), представлен на рис. 3.16. Уравнения состояния и выхода для этого графа, записанные в матричной форме, таковы:
|
'-5 |
0 |
0" |
ї |
|
|
0 |
-2 |
0 |
х + |
1 |
|
0 |
0 |
-3 |
1 |
y(t) = [-20 -10 30] х.
Заметим, что переменную состояния хх мы связали с полюсом S] = -5, х2 — с полюсом s2 и х3 — с полюсом s3, как показано на рис. 3.16. Индексация переменных состояния в данном случае является произвольной; например, х{ мы могли бы выбрать связанной с полюсом s = —2.
Развязывание переменных состояния в случае различных полюсов —Sj, - s2, приводит к тому, что в уравнении состояния матрица А приобретает диагональную, или каноническую форму. Если же среди полюсов системы имеются кратные, то все, что можно сделать, — это представить матрицу А в блочно-диагональной форме, известной как жорданова каноническая фор - Рис_ 316. Сигнальный граф
ма. с развязанными переменными состояния
|
|
|
Y(s) |
(3.54)
Пример 3.2. Распространение эпидемического заболевания
Распространение эпидемического заболевания можно описать системой дифференциальных уравнений. Исследуемое население делится на три группы — х2 и л3, так что группа*, вос
приимчива к эпидемическому заболеванию, группах2 инфицирована, а группах, исключается из первоначального числа исследуемых. Исключение х3 происходит по причине иммунизации, смерти или изоляции от xv Данная система содержит обратные связи и может быть описана следующими уравнениями:
dx,
—1 = - оис, - |«2 + Ц(ч-
dt
|
Ух2 + г<2(0- |
|
£&3 dt |
^ = Вх ■ dt 1
= CCXj + ух2 ■
|
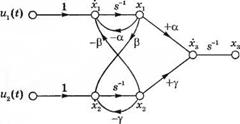
Рис. 3.17. Сигнальный граф, отражающий распространение эпидемического заболевания |
Скорость, с которой появляются новые восприимчивые к заболеванию, равна к,(<), а скорость, с которой появляются новые инфицированные, равна u2(t). В изолированном сообществе И](0 = = u2(t) = 0. Интересно отметить, что эти же уравнения могут описывать и распространение в обществе информации или новой идеи.
|
(3.55) |
В данной системе мы имеем физические переменные состояния *[, х2 и х3. На рис. 3.17 изображен сигнальный граф, отражающий систему дифференциальных уравнений. Уравнение состояния в векторно-матричной форме имеет вид:
|
xi |
1! |
-Р |
0' |
X, |
1 |
0' |
||||||
|
d |
0 |
0 |
1 |
4V) |
||||||||
|
х2 |
Р |
-у |
х2 |
+ |
||||||||
|
dt |
0 |
0 |
0 |
ib(t) |
||||||||
|
.х3. |
a |
У |
.*3. |
Анализ уравнения (3.55) и сигнального графа показывает, что переменная состояния х3 зависит от X] и хг, но не оказывает на них влияния.
Рассмотрим изолированное сообщество, в котором nx(t) = n2(t) = 0. Положению равновесия системы в пространстве состояний соответствует dxldt = 0. Анализ уравнения (3.55) показывает, что система будет находиться в равновесии при хх = х2 = 0. Чтобы определить, прекратится ли в сообществе эпидемическое заболевание, нам необходимо получить характеристическое уравнение системы. Сигнальный граф на рис. 3.17 содержит три контура, два из которых не касаются друг друга, поэтому определитель графа
Д(ї) = 1 - (- Ш'1 — уs~l - pV“) + ays 2 . (3.56)
Таким образом, характеристическое уравнение имеет вид:
|
(3.57) |
q(s) = ї2Д(ї) = s2 + (а + y)s + (ay + p2) = 0.
Поскольку (a + у)>0 и (ay + P")>0, то корни этого характеристического уравнения лежат в левой половине s-плоскости и, следовательно, свободное движение системы при t —» оо стремится к нулю.
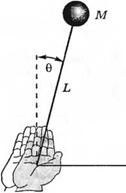
Пример 3.3. Управление перевернутым маятником
Нарис. 3.18 проиллюстрирована проблема балансирования палки с шариком, находящейся на ладони человека. Палка будет находится в равновесии только если 0(0 = 0 и dQ/dt = 0. Эта проблема по сути ничем не отличается от управления положением ракеты на начальной стадии полета. Эта проблема классически моделируется в виде перевернутого маятника, смонтированного на тележке, как показано на рис. 3.19. Тележка должна двигаться таким образом, чтобы масса т всегда занимала вертикальное положение. В качестве переменных состояния естественно принять угол отклонения маятника 0(0 и перемещение тележки y{t). Дифференциальные уравнения, описывающие движение данной системы, можно получить.-записав выражения для суммы сил, действующих в горизонтальном направлении, и суммы моментов относительно точки вращения. Будем считать, что М» т и угол отклонения от вертикали 0 является малым, поэтому уравнения являются линейными. Сумма сил, действующих в горизонтальном направлении, равна
Му + тів - a(t) = 0, (3.58)
где и(0 — сила, приложенная к тележке, а /—расстояние от массы т до точки вращения. Сумма моментов относительно точки вращения равна
ml у + т12в — mlgQ = 0. (3.59)
Переменные состояния для двух уравнений второго порядка выберем как (*,. х2. л3. х4) = (у. > 0, 0).Тогда уравнения (3.58) и (3.59) можно записать с учетом этих переменных состояния:
Мх2 + mlx4 - u(t) = 0 (3.60)
и
х2 + 1хл - gxз = 0. (3.61)
Чтобы получить необходимые дифференциальные уравнения первого порядка, выразим из (3.61) I х4 и подставим его в (3.60):
Мх2 + mgx3 = u(t (3.62)
где учтено, что М» т. Далее, подставляя х2 из (3.60) в (3.61), получим:
Mlx4 - MgXj + u(t) = 0l (3.63)
|
ладони |
|
Рис. 3.18. Перевернутый маятник на ладони человека. Для простоты полагают, что движение происходит в одной плоскости |
|
Движение |
|
|
|
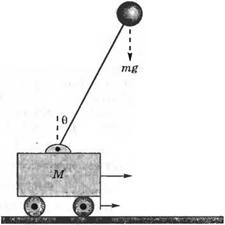
Рис. 3.19. Перевернутый маятник на тележке |
|
ту |
|
Масса т |
|
u(t) Поверхность y(t) без трения |
|
|
|
u(t) |
Таким образом, четыре дифференциальных уравнения первого порядка будут иметь вид:
mg 1 . ,
X, = X-,. Хп —----------------- Х-,--- н - u(t),
12 2 М М
|
(3.64) |
|
Отсюда получаем матрицы системы: |
|
(3.65) |
|
"0 |
1 |
0 |
O' |
0 |
|
|
0 |
0 |
-(mg/M) |
0 |
; в = |
УМ |
|
0 |
0 |
0 |
1 |
0 |
|
|
0 |
0 |
g/1 |
0 |
-УМІ |
|
х? — Хл. х,=—х%---- — u(t). 3 4 4 I 3 Ml |
|
А = |