СОВРЕМЕННЫЕ СИСТЕМЫ УПРАВЛЕНИЯ

Чувствительность систем управления к изменению параметров

Объект управления, представленный передаточной функцией G(s), какова бы ни была его природа, подвержен влиянию окружающей среды, старению, отсутствию точной информа­ции о его параметрах и других объективных факторов, которые негативно сказываются на его поведении. В разомкнутой системе все эти факторы приводят к отклонению выходной переменной от желаемого значения. Замкнутая система, напротив, чувствует это отклоне­ние, обусловленное изменениями параметров объекта, и пытается скорректировать выход­ную переменную. Поэтому чувствительность системы управления к изменению парамет­ров есть вопрос первостепенной важности. Основное преимущество систем с обратной свя­зью состоит в их способности снижать чувствительность к изменению параметров.

В случае замкнутой системы, если GH(s) » 1 для всех представляющих интерес зна­чений комплексной частоты, то из (4.2) мы имеем:

У(,)--1_Л(,). (4.4)

H(s)

Следовательно, выход определяется только передаточной функцией H(s), которая может быть и константой. Если H(s) = 1, то мы в точности достигаем желаемого результата, т. е. выход становится равным входу. Однако прежде чем использовать эту идею для синтеза
систем управления, мы должны заметить, что условие G(s)H(s)» 1 может привести к тому, что реакция системы будет сильно колебательной или даже к потере системой устойчиво­сти. Но, тем не менее, тот факт, что увеличивая модуль функции G(s)H(s), мы уменьшаем влияние изменений в G(s) на выходную переменную, является исключительно ценным. Та­ким образом, первым преимуществом системы с обратной связью является то, что в ней уменьшается влияние изменений параметров объекта управления.

Чтобы проиллюстрировать сказанное выше, рассмотрим случай, когда за счет изме­нения параметров объекта его передаточная функция приняла выражение G(s)+AG(s). Тогда, если система является разомкнутой, выходная переменная (в виде изображения по Лапласу) получит приращение

A Y(s) = A G(s)R(s). (4.5)

В замкнутой системе мы имеем:

У(і)+АУ(і) =---------------------- S(s)+AG(a) R{$)-------------------------------------- (4 6)

l + [G(s) + AG(s)]H(s)

Отсюда приращение выходной переменной:

А У (5) =---------------------------------------------- R{s). (4.7)

[1 + GH(s) + AG ОД][1 + GH(s)]

Если GH(s)» AGH(s), как это часто имеет место, то

AY(s) = А-(Д) ,.Д(д). (4.8)

[1+СОД]2

Анализ выражения (4.8) показывает, что в замкнутой системе изменение выходной пе­ременной уменьшается в [l+G//(i)] раз; в свою очередь член [l+G//(s)j обычно много больше единицы в представляющем интерес диапазоне комплексной частоты. Сомно­житель 1 +GH(s) играет очень важную роль в определении характеристик систем с об­ратной связью.

Чувствительность системы определяется как отношение процентного изменения передаточной функции системы к процентному изменению передаточной функции объ­екта. Система имеет передаточную функцию

= (4.9)

R(s)

и, следовательно, чувствительность определяется, как

s _ AT(s)/T(s) AG(s)/G(s)'

В пределе, переходя к малым изменениям, (4.10) приводится к виду:

_ дТ/Т _ д In Т ~ dG/G ~ Sin G

Чувствительность системы — это отношение изменения ее передаточной функ­ции к изменениям передаточной функции (или параметров) объекта управле­ния при условии их малости.

Из (4.5) следует, что чувствительность разомкнутой системы равна единице. Чувст­вительность замкнутой системы легко можно получить из (4.11). Замкнутая система име­ет передаточную функцию

T(s)= С(Д) . l + GH(s)

Следовательно, ее чувствительность равна

е? _дТ G 1 G

--

dG Т (1 +GHf G!{ + GH)

или

(4.12)

1 + G(.s)tf(.s)

Отсюда еще раз видно, что чувствительность замкнутой системы можно сделать меньше, чем ее чувствительность в разомкнутом состоянии, путем увеличения GH(s) в представля­ющем интерес диапазоне частот.

Чувствительность замкнутой системы к изменению передаточной функции элемента обратной связи H(s) равна

дТ Н ~дН Y

(4-13)

1+ GH) G/(l+GH) l + GH

Если произведение GH достаточно велико, то чувствительность близка к единице и изменения передаточной функции H(s) непосредственно сказываются на выходной пере­менной. Поэтому в качестве элементов обратной связи необходимо выбирать такие, кото­рые обладали бы стабильными характеристиками, не зависящими от внешних факторов.

Часто бывает необходимо определить чувствительность, где а — параметр пере­даточной функции G(s). Используя правило дифференцирования сложной функции, мож­но записать:

SI Sca. (4.14)

Встречаются также случаи, когда передаточная функция системы T{s) имеет вид дроби:

T{s, а) = ^Ц, (4.15)

D(s, а)

где а—параметр, подверженный изменениям за счет внешних факторов. Тогда чувствите­льность системы к изменению а можно записать, используя выражение (4.11):

где а0 — номинальное значение параметра.

Способность уменьшать влияние изменения параметров путем введения обратной связи — одно из положительных качеств замкнутых систем управления. Чтобы добиться высокой точности управления в разомкнутых системах, необходимо очень тщательно подходить к выбору элементов, образующих передаточную функцию G(s). Напротив, замкнутые системы допускают определенные вариации параметров G(s), поскольку их влияние ослабляется в 1 +GH(s) раз. Это свойство замкнутых систем лежит в основе про­ектирования электронных усилителей, используемых в каналах связи. Мы проиллюстри­руем данный факт на простом примере.

Пример 4.1. Усилитель с обратной связью

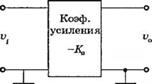
Во многих практических приложениях используется усилитель, имеющий коэффициент уси­ления - Ка, как показано на рис. 4.4(a). Выходное напряжение равно

vo = -*>,. (4.17)

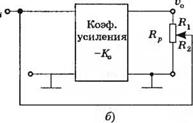
Часто с помощью потенциометра вводится обратная связь, как показано на рис. 4.4(6). Усили­тель без обратной связи имеет передаточную функцию

Т=-Ка,

и ее чувствительность к изменению коэффициента усиления равна

Si =1.

а)

Рис. 4.4. (а) усилитель; (б) усилитель с обратной связью

-► 1>0 Структурная схема усилителя с обратной связью приве­дена на рис. 4.5, где

Р = ^ (42°)

Я

Рис. 4.5. Структурная схема усилителя с обратной связью при Rp » /?0

Передаточная функция усилителя с обратной связью равна

т ка

1 +К£'

а ее чувствительность к изменению Ка определяется как

Rp = Ri + /?2-

1

(4.23)

" 1+^0P

Если Ка достаточно велико, то чувствительность является малой. Например, если

Ка= 104, Р = 0,1, (4.24)

то

1

1+ 10J

что практически в 1000 раз меньше, чем для усилителя без обратной связи.

К понятию чувствительности мы еще вернемся в последующих главах, чтобы подчеркнуть его особую важность при синтезе и анализе систем управления.