ПЕРЕРАБОТКА СЫПУЧИХ МАТЕРИАЛОВ В. МАШИНАХ БАРАБАННОГО ТИПА

СЕГРЕГАЦИЯ ПОЛИДИСПЕРСНОГО МАТЕРИАЛА

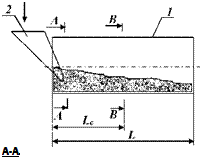
Как известно [30, 31], при движении полидисперсного материала в поперечном сечении барабана на­блюдается сегрегация частиц по размерам. В результате этого мелкие частицы концентрируются вокруг центра циркуляции [24]. На рис. 8.13 схематически показано распределение сыпучего материала вдоль оси трубы и в двух поперечных сечениях, расположенных на разных расстояниях от загрузочного края трубы.

Разделим условно циркуляционный контур на две зоны 1 к 2. Если в воронку 2 загружается смесь из крупных частиц В и мелких Л, то можно считать, что в сечении А-А концентрации частиц 4иВв зонах 1 и 2 будут одинаковыми и равными их концентрациям в исходной смеси. В процессе циркуляции частиц в поперечном сечении вращающейся трубы 7 и их продвижения вдоль оси этой трубы мелкие частицы будут концентрироваться в зоне 2. Таким образом, в сечении 7>-7> концентрация мелких частиц в зоне Сбудет больше, чем в сечении А-А.

Скорость осевого движения частиц уменьшается по мере приближения к центру циркуляции, сле­довательно, в результате сегрегации мелкие частицы будут иметь меньшую осевую скорость, чем круп­ные. Можно предположить, что при дозировании полидисперсного материала мелкие частицы будут накапливаться во вращающейся трубе. Предварительные экспериментальные исследования по сравне­нию гранулометрического состава полидисперсного материала на входе и на выходе из нее подтвердили данное предположение. Действительно, в начале процесса дозирования содержание мелкой фракции в пробах на выходе из вращающейся трубы было меньше, чем в исходном материале.

Рис. 8.13. Схема образования ядра сегрегации

В дальнейшем наблюдается неравномерный выход мелкой фракции из трубы. Поскольку грануломет­рический состав материала существенно влияет на его насыпную плотность, эффект сегрегации должен отрицательно сказываться на точности непрерывного дозирования. Эффект сегрегации наблюдается и при движении частиц с разной удельной плотностью [32, 33].

Известны различные способы [34], в том числе и конструктивные [35, 36], которые позволяют ми­нимизировать отрицательный эффект сегрегации. При дозировании полидисперсного материала наибо­лее приемлемым является устройство [35, 37] для периодического разрушения ядра сегрегации, образо­ванного мелкими частицами.

При теоретическом описании и математическом моделировании процесса сегрегации полидисперс­ного материала во вращающейся трубе будем учитывать, что конструкция устройства для разрушения ядра сегрегации позволяет целенаправленно перемещать частицы из одной зоны в другую. Таким обра­зом, для минимизации нежелательного влияния сегрегации на точность непрерывного дозирования не­обходимо знать, когда и где (по длине трубы) образуется устойчивое ядро сегрегации.

Известны различные подходы к рассмотрению явления сегрегации и математические модели, описы­вающие этот процесс [38 - 42].

В основу математического описания процесса сегрегации с периодическим разрушением ядра из мелких частиц может быть положена послойная модель, предложенная в работах [24, 25]. Согласно данной модели, материал в поперечном сечении вращающегося барабана разбивается на п циркуляци­онных подслоев с равной производительностью, т. е. границы раздела подслоев определяются с исполь­зованием следующего соотношения [24]:

Ц^І^-ІЇ+ЛсУл]0-5, (8.38)

где п - количество подслоев; Rj - радиус наружной границы /-го подслоя.

Процесс рассматривается как периодический в пространстве и времени с использованием матема­тического аппарата случайных марковских процессов. Допущение о дискретности в пространстве обос­новывается тем, что сегрегация наблюдается только в скатывающемся слое. Дискретным во времени процесс можно считать потому, что частицы лишь периодически попадают в скатывающийся слой. По­скольку при реализации технологии двухстадийного дозирования распределение материала по длине трубы изменяется во времени с периодом А Т, послойная модель нуждается в модернизации. Будем счи­тать, что начальное состояние системы нам известно, т. е. мы знаем, какое количество сыпучего мате­риала Vj находится на каждом участке и как фракции этого материала или ключевой компонент распре­делен по подслоям в пределах каждого участка, т. е. знаем Q у о - Концентрация ключевого компонента (мелких частиц) в любом подслое Уна участке j в момент времени Т= к А Т можно рассчитать, используя следующие зависимости:

PUM=P(^-CMJ^), Рі-и, і = Р^-Сим), (8.40)

где V- объем материала на участке; С - концентрация ключевого компонента в подслое; j - номер уча­стка; У - номер подслоя.

Фактически зависимости (8.39, 8.40) представляют собой математическую модель процесса сегре­гации полидисперсного материала при его движении в гладком вращающемся перфорированном бара­бане. Последовательно изменяя значения У: от 1 до m, j от 1 до N и У от 1 до /7, можно рассчитать распре­деление ключевого компонента вдоль оси барабана и в поперечном сечении каждого участка в любой момент времени Т= m А Т.

В отличие от зависимостей, представленных в работах [24, 25], в зависимости (8.39) слагаемое Ujj^k учитывает количество (объем) ключевого компонента, отводимого из данного подслоя или подводимого в него устройством для разрушения ядра сегрегации, а слагаемое И7,; у к учитывает объем ключевого компонента, высыпавшегося через отверстия перфорации на данном переходе [19]. Численное значе­ние у к зависит от геометрических параметров устройства для разрушения ядра сегрегации и режима его работы.

Кроме этого, в предлагаемой модели объемы V)y ^ не постоянны во времени, т. е. зависят от номера перехода Уг, и их численные значения могут быть определены по следующей зависимости:

j, k = 4j, k-l + иик + //о, . (8.41)

где U0, j к - объем основного компонента, подводимого в подслой У участка j на переходе к или отводи­мого из него.

Соответственно будет изменяться объем материала, находящегося на участке j на переходе /у и объ­ем будет равен сумме объемов на участках

£Чкк=ХЫкк-1+и^к)-

Поскольку объемы подслоев изменяются, изменяются также границы между ними и концентрации в образованных подслоях. Методика пересчета границ подслоев и концентраций в них за счет измене­ния суммарного объема материала на участке j достаточно подробно рассмотрена в работе [43].