ПЕРЕРАБОТКА СЫПУЧИХ МАТЕРИАЛОВ В. МАШИНАХ БАРАБАННОГО ТИПА

МОДЕЛИРОВАНИЕ ПРОЦЕССА НЕПРЕРЫВНОЕ© ДОЗИРОВАНИЯ

Поскольку при практическом использовании непрерывных дозаторов необходимо рассчитывать минимальный радиус барабана R, радиус загрузочного отверстия г, максимальный объем отдельной порции, а также время выхода на установившийся режим, было исследовано распределение одной пор­ции во вращающейся трубе. Рассмотрим распределение отдельной порции V, которую загрузили во вращающуюся трубу. Несомненно, что в общем случае загрузка отдельной порции во вращающуюся трубу происходит в течении определенного времени A Tl причем в барабане уже находится некоторое количество материала, однако, как будет показано ниже, эти особенности легко учесть если иметь ре­шение предложенного варианта.

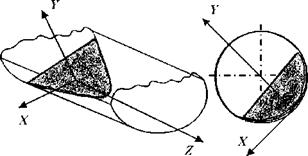
Пусть внутренний радиус барабана равен R, а его длина - L. На рис. 8.14 показано распределение первой порции в пустой горизонтальной вращающейся трубе.

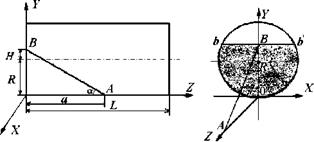
Для вычисления параметров распределения порции материала воспользуемся схемами, показанны­ми на рис. 8.15. Объем первой порции во вращающейся трубе можно определить следующим образом:

V^jjzdxc. (8-43)

D

Уравнение плоскости, с которой совпадает открытая поверхность сыпучего материала, имеет вид:

Z= a — yctga, (8.44)

^изменяется от 0 до a-tga

Уравнение области D(рис. 8.15):

откуда получаем границы изменения х

от [я2-(у-я)2]0,5 до [я2 - (у - Я)2]°5 = Кх

С учетом (8.44) и (8.45) интеграл можно записать следующим образом:

подставив Kx = [я2 -(у-я)2]0’5 и введя обозначение atga-R = Н, после преобразований получим [19]:

При проектировании трубчатого преобразователя порций формула (8.47) позволяет при известном значении Еподобрать рациональные значения радиуса трубы R и радиуса входного отверстия г= Н. Ес­ли решается вопрос поиска оптимальных режимных параметров для уже имеющейся конструкции бара­банного преобразователя, то по формуле (8.47) можно рассчитать максимальный объем отдельной пор­ции.

Учитывая, что уравнение (8.47) аналитически не решается относительно величины Н, при опреде­лении распределения последующих порций, т. е. когда в барабане уже находится некоторое количество материала, использовали численные методы расчета. Рассмотрим алгоритм решения. Схема распреде­ления порции объемом Сна переходе Споказана на рис. 8.16. Считаем, что нам известно распределение сыпучего материала по участкам на переходе k - 1, т. е. известны численные значения V) *- т

Предположим, что объем V на переходе к распределился на М участков, как это показано на рис. 8.16. Учитывая, что открытая поверхность наклонена к оси z под углом трения движения величина стрелки hjk сегмента, который занимает материал на участке У, будет равна:

bit = Кп%к-1 + [фы)+A7/2]tga, . (8.48)

Объем материала А С; к, который добавился на участок I, определим как разность объемов С; к и С; к

- г

Объем С; к определим по следующей формуле:

где So, і, к~ половина центрального угла системы материала на участке Уна переходе У:(см. рис. 8.7).

Найдем расчетное значение объема порции Vp:

Ур=^АЦк. (8.50)

Если Vp > V, то необходимо уменьшить значение Mt, если Vp < V, то увеличить. Как показали ре­зультаты численных экспериментов, целесообразно первоначально принимать Мк = Мк_х. Поскольку зна­чение Мизменяется дискретно, практически невозможно получить Vp = V, поэтому целесообразно уста­навливать следующее ограничение [(к-Кр)/к] < є, где є зависит от числа участков, на которые разделена труба. После выполнения данного условия необходимо провести корректировку значений V) к

Чк^-^Чк - (8.51)

Как отмечалось ранее, для описания процесса непрерывного дозирования полидисперсного мате­риала используем математический аппарат случайных марковских процессов, дискретных в простран­стве и во времени. Трубу по длине разделим на к участков. Будем считать, что система состоит из к+ 1 элементов, где (к + 1)-й элемент показывает, какое количество материала высыпалось из трубы. Со­стояние системы после перехода т определяется вектором состояния Е(т). Координаты вектора есть вероятность нахождения сыпучего материала на участке после перехода т. Данный вектор можно опре­делить, используя следующие соотношения:

Д1) = Д0)Д1);

Е( 2) = Д1)Д2);

(8.52)

ДА) = ДА-1)ДА);

Е(т) = Em - 1 )Д/л),

где ДО) - вектор начального состояния; ДА) - матрица переходных вероятностей на переходе к.

Поскольку рассматривается неустановившийся режим движения сыпучего материала, матрица пере­ходных вероятностей будет изменяться во времени, т. е. элементы матрицы будут разными на разных пе­реходах. Объем материала, находящегося на участке у после перехода к равен объему материала, кото­рый находился на данном участке после перехода к - 1, плюс суммарный объем материала, пришедшего с предыдущих участков, и минус суммарный объем материала, который переместился на последующие участки, т. е.

ЧМ)= V(j, k-l) + A{(j, k)-A$(j, k), (8.53)

где А V (д А) и A Vi(j А) - объемы материала, которые соответственно приходят на участок у или уходят с него на переходе А.

Учитывая, что переход материала может происходить не на один участок, для расчета объема мате­риала на участке у после перехода А получена следующая формула:

j j+Ni

{j, k)={j, m-1)+ ^AV(^)+«(y;m)-s(y;m), (8.54)

^=J~H ^2=7+1

где A V - объем материала, который приходит на данный участок или уходит с него; z - номер преды­дущего участка, с которого материал перемещается на участок у; Z2 - номер последующего участка, на который материал перемещается с участка У; А) - количество предыдущих участков, с которых материал переходит на участок j, N2- количество последующих участков, на которые материал уходит с участка у; ikj’ in) - объем материала, который приходит на участок у на переходе А в результате подачи в барабан очередной порции; s(j А) - объем материала, который приходит на участок у или уходит с него на пере­ходе А в результате перемещения частиц устройством для разрушения ядра сегрегации.

Численные значения s(i, 111) могут быть как положительные, так и отрицательные, и зависят от гео­метрических параметров устройства для разрушения ядра сегрегации и режимов его работы.

Очевидно, что с данного участка может переместиться только часть разницы объемов, находящихся на этом участке и на последующем. Количество участков ушах, на которые произойдет перемещение ма­териала, зависит от угла максимального ската (формула 2.28). Объем материала, который переходит с участка j на переходе к., можно рассчитать по следующей формуле:

Аф-7,)_ ДММ-1)-{j+k-l)llij, k-l)-lij+k-l)} ^ (£ 55)

где Р - параметр математической модели, характеризующий вероятность перехода частиц с одного участка на другой.

Приведенные выше уравнения представляют собой математическую модель процесса преобразова­ния отдельных порций в непрерывный поток в гладком вращающемся барабане. Последовательность использования модели следующая. По формуле (8.47) рассчитывается объем отдельной порции и рас­пределение этой порции по участкам. Используя формулы (8.13) - (8.27), рассчитываются параметры распределения сыпучего материала на каждом участке. По формулам (8.35) - (8.36) определяется угол максимального ската и участки, на которых происходит перераспределение материала при осевом дви­жении частиц. Далее, последовательно изменяя к от 1 до т= Т/ Ах, j от 1 до N+ 1, рассчитываются рас­пределение зернистого материала вдоль оси барабана в любой момент времени Ти количество материа­ла, которое высыпается из барабана. Следует особо отметить, что расчет распределения сыпучего мате­риала в поперечном сечении каждого участка осуществляется на каждом переходе. При переходах, кратных АТ/Ах, производится расчет распределения новой порции по участкам. Формирование проб для прогнозирования точности дозирования осуществляется путем суммирования объемов на участке N+ 1 за А7пР/Ах переходов.

Поскольку перемещение частиц вдоль оси происходит при их движении только в скатывающемся слое, естественно предположить, что время одного перехода прямо пропорционально времени Хц, за ко­торое совершается один цикл циркуляции сыпучего материала в поперечном сечении барабана, т. е.

Ах = Р2хц, (8.56)

где Р1 - коэффициент пропорциональности.

Численное значение хц легко определить, если известно распределение сыпучего материала в попе­речном сечении барабана. Учитывая, что материал распределяется не равномерно по длине барабана, целесообразно использовать среднее значение хц для N участков за АТ/Ах переходов. Таким образом, в рассмотренной математической модели два параметра {Р, Р1) подлежат идентификации.

Как отмечалось выше, при расчете процесса двухстадийного дозирования необходимо учитывать погрешность порционного дозирования, отклонения насыпной плотности и углов трения сыпучих мате­риалов. Это можно сделать с помощью имитационного моделирования. В основу имитационной моде­ли положена математическая модель, представленная в предыдущем разделе. Имитация указанных вы­ше отклонений осуществлялась с помощью генератора случайных чисел и фильтров, которые позволя­ют учитывать распределение отклонений параметров. В качестве примера рассмотрим имитацию по­грешностей порционного дозатора. Данная модель позволяет не только рассчитывать процесс преобра­зования отдельных порций в непрерывный поток, но и прогнозировать точность дозирования с учетом конкретных условий реализации данного процесса. На рис. 8.17 показана гистограмма отклонений порци­онного дозатора, построенная по результатам его тестирования. Как видно из гистограммы, 60 % анали­зируемых порций имели нулевое отклонение от заданных значений, 5 % имели отклонения -0,5 %, 5 % имели отклонения +0,5, 15% имели отклонения -0,25 %, 15 % имели отклонения +0,25 %. В данном слу­чае фильтр работает следующим образом. Если генератор случайных чисел выдает значение

от 0 до 0,05, то вес порции равен 1,005А/> Если выдается значение от 0,05 до 0,2, то вес порции равен 1,0025АР и т. д. Аналогичным образом имитировали отклонения насыпного веса сыпучего материала в отдельных порциях от номинального значения, а также возможные отклонения в значениях углов тре­ния покоя и движения.

Данная модель позволяет не только рассчитывать процесс преобразования отдельных порций в не­прерывный поток, но и прогнозировать точность дозирования с учетом конкретных условий реализации данного процесса.